
- •3 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
- •Основы гидравлики
- •Содержание
- •Рабочая программа
- •Введение
- •Гидростатика
- •Основные физические свойства жидкости и газа.
- •Вязкость жидкости.
- •Силы, действующие в жидкости
- •Абсолютное Гидростатическое давление и его свойства
- •Дифференциальные уравнения равновесия жидкости
- •Поверхность равного давления и ее свойства
- •Основное уравнение гидростатики
- •Приборы для измерения абсолютного, манометрического давлений и давления вакуума
- •Сила давления жидкости на наклонную плоскую стенку
- •Точка приложения силы давления жидкости на плоские стенки.
- •Сила давления жидкости на криволинейные поверхности
- •Примеры и задачи
- •Основы кинематики и динамики жидкости
- •Основные понятия и определения гидродинамики
- •Уравнение неразрывности потока
- •Уравнение Бернулли для струйки идеальной жидкости
- •Уравнение Бернулли для струйки и потока реальной жидкости
- •Интерпритации уравнения Бернулли
- •Примеры и задачи
- •Гидравлические сопротивления
- •Виды гидравлических сопротивлений
- •Ламинарное и турбулентное движение жидкости
- •Основное уравнение равномерного движения
- •Ламинарный режим движения
- •Турбулентный режим движения
- •Экспериментальные исследования коэффициента гидравлического сопротивления
- •Примеры и задачи
- •Гидравлический расчет трубопроводов
- •Расчет Коротких трубопроводов
- •Уравнение простого трубопровода
- •Первый тип расчета
- •Второй тип расчета
- •Третий тип расчета
- •Расчет газопроводов при малых перепадах давлений
- •Примеры и задачи
- •Расчет газопроводов при Больших перепадах давлений
- •Гидравлический удар в трубах
- •Примеры и задачи
- •Гидравлический расчет истечения жидкостей
- •Истечение жидкости из малого отверстия в тонкой стенке
- •Истечение жидкости через внешний илиндрический насадок.
- •Примеры и задачи
- •Гидравлические элементы живого сечения потока в канале.
- •Основные расчетные формулы для открытых русел
- •Основные задачи при расчете трапецеидальных каналов на равномерное движение воды.
- •Расчет безнапорных труб
- •Примеры и задачи
- •Литература
Уравнение Бернулли для струйки идеальной жидкости
Для вывода уравнения Бернулли используется теорема об изменения кинетической энергии - изменение кинетической энергии равно работе внешних сил.
|
Р |
|
|
(3.0) |
dV - объём массы жидкостиdm.
Тогда изменение кинетической энергии dЭкинравно
|
|
(3.0) |
При движении от первого сечения ко второму на массу действует сила тяжести, поэтому изменение работы сил тяжести dAтяжравно:
|
|
(3.0) |
На поперечное сечение dсо стороны окружающей жидкости действует сила давленияdP = p d. За времяdtмасса частицы жидкости перемещается на расстояниеdS, тогда работа, совершаемая силами давления, равнаdAдав = dP dS = p d dS = p dV(d dS = dV– объем частицы жидкости). Поэтому работа сил давления равна
|
|
(3.0) |
В общем случае на боковой поверхности элементарной струйки действуют силы трения, которые противодействуют движению жидкости. В данном случае рассматривается идеальная жидкость, вязкость которой равна нулю, поэтому сил трения равны нулю и работы не совершают.
Используя теорему изменения кинетической энергии, запишем:
|
|
(3.0) |
или
|
|
(3.0) |
Разделим это выражение на вес частицы жидкости, которая проходит за время dtчерез сечение струйки,dG=gdm= ρgdV:
|
|
(3.0) |
Так, как сечения 1-1 и 2-2 были выбраны произвольно, то последнее уравнение можно переписать в виде:
|
|
(3.0) |
Уравнение (3.24) или (3.25) называется уравнением Бернулли. Уравнение Бернулли в таком виде можно записать только для установившегося движения несжимаемой идеальной жидкости. Уравнение Бернулли выражает закон сохранения энергии – для идеальной жидкости полная энергия вдоль элементарной струйки сохраняется. В уравнения (3.24) и (3.25) входит не сама энергия, а энергия отнесённая к весу частицы жидкости, которая называется удельнойэнергией, поэтому каждое слагаемое в уравнении Бернулли представляет собой удельную потенциальную энергию положения, удельную потенциальную энергию давления и удельную кинетическую энергию и в системе СИ измеряется в метрах. Сумма этих энергий называется полной удельной энергией.
Уравнение Бернулли для струйки и потока реальной жидкости
Если по элементарной струйке движется реальная жидкость, то возникают силы трения и часть полной механической энергии переходит в тепловую энергию, которая в уравнении (3.24) не учитывается. Поэтому полная механическая энергия в начале струйки будет больше, чем в конце. Потерей напораилипотерей полной удельной энергии h1-2- называется разность полных удельных энергий в начале и в конце элементарной струйки.
|
|
(3.0) |
Тогда уравнение для элементарной струйки реальной жидкости запишется:
|
|
(3.0) |
Рассмотрим поток жидкости. Поток жидкости состоит из элементарных струек, скользящих друг относительно друга с разными скоростями. Пусть за время dt = 1через поперечное сечение элементарной струйки проходит массаdm = u d. Осредним уравнение Бернулли для элементарной струйки реальной жидкости по поперечному сечению. Так, как в поперечном сечении давление распределяется по гидростатическому закону, сумма первых двух слагаемых постоянна и при осреднении не изменится. Усредняя третье слагаемое и выражая его через среднюю скорость, получим
|
|
(3.0) |
Тогда для потока реальной жидкости уравнение Бернулли запишется:
|
|
(3.0) |
z– расстояние от плоскости сравнения до любой точки поперечного сечения, м;
p– давление именно в этой точке, Па;
v– средняя скорость в данном поперечном сечении, м/с;
– имеет три названия: коэффициент неравномерности распределения скоростей, средняя коэффициент Кариолиса, коэффициент кинетической энергии.
Коэффициент неравномерности распределения скоростей определяется
|
|
(3.0) |
Коэффициент неравномерности распределения скоростей определяется в зависимости от режимов движения жидкости
|
Ламинарный режим |
Турбулентный режим |
V |
|
|
|
|
|
=2 |
=1,11,2 |
=1 |
На практике обычно выбирают значение = 1.
При применении уравнения Бернулли следует придерживаться следующих правил:
Выбрать два поперечных сечения. Поперечные сечения выбираются по направлению движения жидкости в начале потока 1 – 1 в конце 2 - 2. Поперечные сечения выбираются там, где известны давления или где одно из давлений необходимо найти.
Выбирают плоскость сравнения 0 - 0. Плоскостью сравнения может служить любая горизонтальная поверхность. Обычно выбирают плоскость сравнения, проходящую через центр тяжести нижнего поперечного сечения.
Записывают значения zиpдля поперечных сечений. Для напорных потоков (движение жидкости в трубе) за характерную точку обычно принимают центр тяжести трубы. Для безнапорных потоков (движение жидкости в реке) за характерную точку обычно принимают точку на свободной поверхности жидкости. Давлениеpдолжно иметь один и тот же тип или абсолютное в обеих частях уравнения или манометрическое.
Расписывают скорости в поперечных сечениях. В уравнении Бернулли, как минимум, входят три скорости: v1– средняя скорость в первом сечении,v2– средняя скорость во втором сечении,v– средняя скорость в трубе, которая соединяет эти сечения (от этой скорости зависят потери напора h1-2). Если известен расход, то скорости находятся:
|
|
(3.0) |
Если расход неизвестен, то неизвестны и скорости. В этом случае удобно все скорости выразит через скорость в трубе:
|
|
(3.0) |
Полученные значения z, p, vподставляют в уравнение Бернулли и находят неизвестную величину.

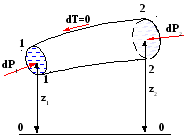 ис.3.23 – силы действующие
на элементарную струйку
ис.3.23 – силы действующие
на элементарную струйку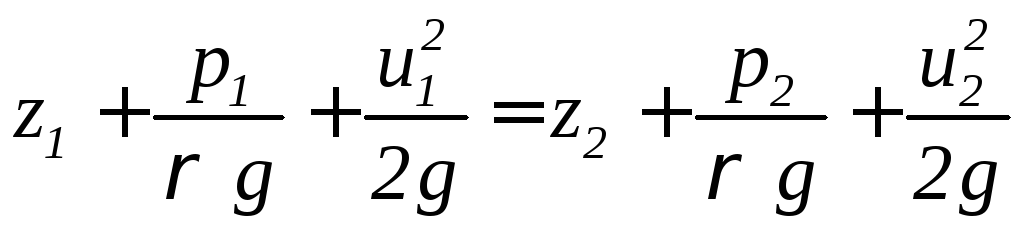 .
. .
.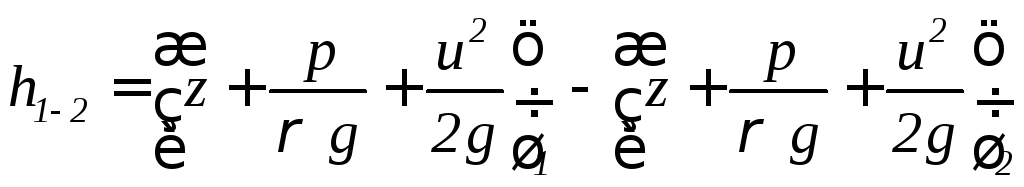 .
.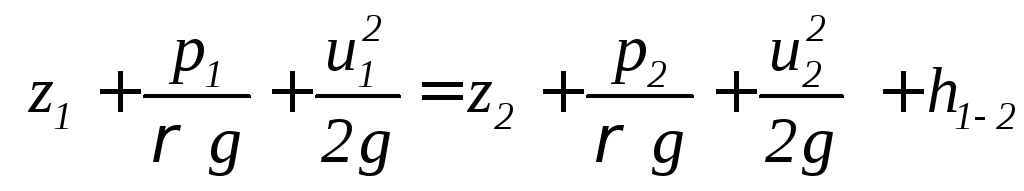 .
. .
. .
.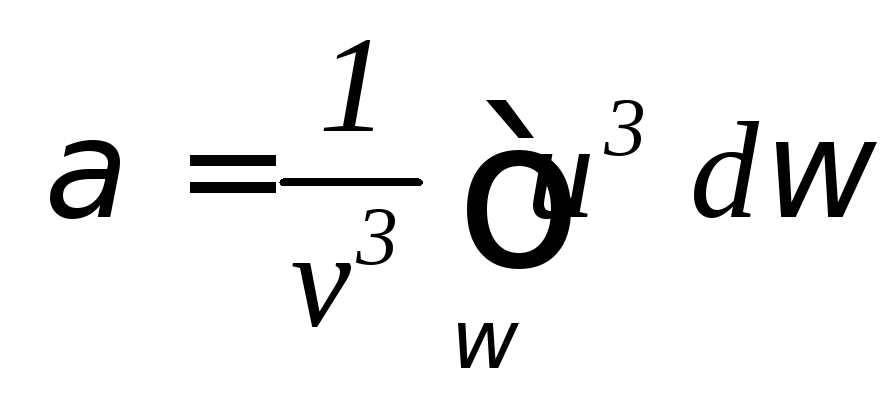 .
.


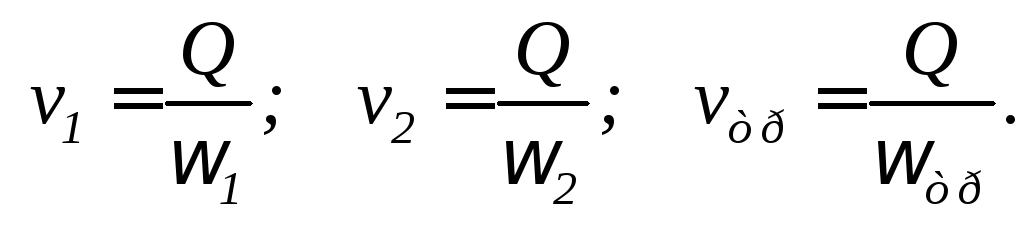 .
. .
.