- •3 Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования
- •Основы гидравлики
- •Содержание
- •Рабочая программа
- •Введение
- •Гидростатика
- •Основные физические свойства жидкости и газа.
- •Вязкость жидкости.
- •Силы, действующие в жидкости
- •Абсолютное Гидростатическое давление и его свойства
- •Дифференциальные уравнения равновесия жидкости
- •Поверхность равного давления и ее свойства
- •Основное уравнение гидростатики
- •Приборы для измерения абсолютного, манометрического давлений и давления вакуума
- •Сила давления жидкости на наклонную плоскую стенку
- •Точка приложения силы давления жидкости на плоские стенки.
- •Сила давления жидкости на криволинейные поверхности
- •Примеры и задачи
- •Основы кинематики и динамики жидкости
- •Основные понятия и определения гидродинамики
- •Уравнение неразрывности потока
- •Уравнение Бернулли для струйки идеальной жидкости
- •Уравнение Бернулли для струйки и потока реальной жидкости
- •Интерпритации уравнения Бернулли
- •Примеры и задачи
- •Гидравлические сопротивления
- •Виды гидравлических сопротивлений
- •Ламинарное и турбулентное движение жидкости
- •Основное уравнение равномерного движения
- •Ламинарный режим движения
- •Турбулентный режим движения
- •Экспериментальные исследования коэффициента гидравлического сопротивления
- •Примеры и задачи
- •Гидравлический расчет трубопроводов
- •Расчет Коротких трубопроводов
- •Уравнение простого трубопровода
- •Первый тип расчета
- •Второй тип расчета
- •Третий тип расчета
- •Расчет газопроводов при малых перепадах давлений
- •Примеры и задачи
- •Расчет газопроводов при Больших перепадах давлений
- •Гидравлический удар в трубах
- •Примеры и задачи
- •Гидравлический расчет истечения жидкостей
- •Истечение жидкости из малого отверстия в тонкой стенке
- •Истечение жидкости через внешний илиндрический насадок.
- •Примеры и задачи
- •Гидравлические элементы живого сечения потока в канале.
- •Основные расчетные формулы для открытых русел
- •Основные задачи при расчете трапецеидальных каналов на равномерное движение воды.
- •Расчет безнапорных труб
- •Примеры и задачи
- •Литература
Основы кинематики и динамики жидкости
Основные понятия и определения гидродинамики
Местная скорость–u– скорость движения частицы жидкости в данной точке потока. Местная скорость зависит от координат точкиx, y, zи времениt.
Давление в данной точке потока pтакже зависит от координат этой точки и время. Поэтому
|
|
(3.0) |
Для решения гидродинамической задачи необходимо найти распределение давления pи составляющих вектора скоростиux, uy, uzв пространстве в любой момент времени. Движение называетсяустановившемся, если давлениеpи скоростиuне зависит от времени.В противном случае, движение называетсянеустановившемся (нестационарным).
|
Р |
|
Р |
Трубкой тока - называется поверхность, образованная линиями тока проведёнными через бесконечно малый замкнутый контур (рис. 3.3).
|
Р |
Элементарная струйка- называется движения жидкости, ограниченная трубкой тока.
Потоком жидкости - называется совокупность элементарных струек, скользящих друг относительно друга (рис. 3.4).
Поток называется напорным, если боковая поверхность потока ограничена твёрдыми стенками, в этом случае движение происходит, в основном, за счёт перепада давления - движение в трубе.
Поток называется безнапорным, если имеет поверхность, на которой давление постоянно, в этом случае движение происходит за счёт сил тяжести (движение в реке).
|
Р |
|
Р |
Р |
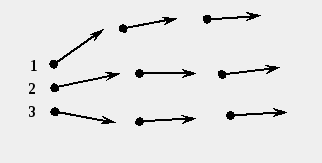
Поперечным сечением потока называется поверхность проведения перпендикулярно направлению скорости (рис. 3.7). На рис. 3.7 обозначения 1-1, 2-2, 3-3 являются поперечными сечениями.Свойство поперечного сечения– в поперечном сечении давление изменяется по гидростатическому закону:
|
p = p0 + g (z0 – z). |
(3.0) |
Или
|
|
(3.0) |
|
Р |
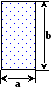
Некоторые виды поперечных сечений их характеристики приведены на рисунке 3.8.
|
Трубопровод |
Вентиляционный канал |
Безнапорный канал |
Кольцевое пространство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.21. Некоторые поперечные сечения потока и их характеристики. | |||
Смоченным периметром- называется часть периметра поперечного сечения, где жидкость соприкасается с твёрдыми стенами.
Гидравлическим радиусом R- называют отношение площади поперечного сечения к смоченному периметруR=/.
Эквивалентным диаметром- называется учетверённый гидравлический радиусdэ= 4R. Эквивалентным диаметром или гидравлическим радиусом используется при расчёте движения жидкости в потоках, когда поперечное сечение не является круглой трубой. Например, при расчёте вентиляционных каналов, теплообменных аппаратов и т.д. В этом случае в формулах расчёта потерь напора по длинеhд, числаReи коэффициент гидравлического сопротивления трениявместо диаметраDподставляется эквивалентный диаметрdэ.
|
|
(3.0) |
При расчёте давления жидкости в каналах обычно используется гидравлический радиус.
Объемным расходом Qназывается объем жидкости прошедший через поперечное сечение за единицу времени.
|
|
(3.0) |
Массовым расходом Qmназывается масса жидкости прошедшая через поперечное сечение за единицу времени.
|
|
(3.0) |
Массовый расход равен произведению плотности на объемный расход:
|
|
(3.0) |
Средней скоростью vназывается отношение объемного расхода жидкости к площади поперечного сечения.
|
|
(3.0) |
Если объединить последние два уравнения, получим для массового расхода выражение
|
|
(3.0) |


 ис.3.14 – поле скоростей
ис.3.14 – поле скоростей ис.3.15 – линия тока
ис.3.15 – линия тока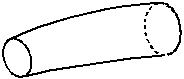 ис.3.16 – Трубка тока
ис.3.16 – Трубка тока ис.3.17 – Поток жидкости
ис.3.17 – Поток жидкости ис.3.18-Равномерное
движение
ис.3.18-Равномерное
движение 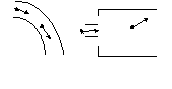 ис.3.19 -
Неравномерное движение
ис.3.19 -
Неравномерное движение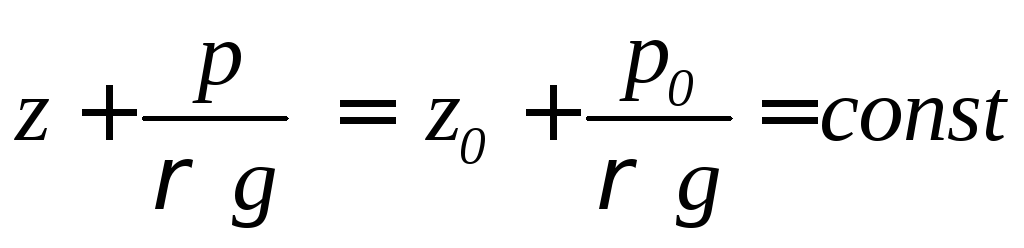 .
. ис.3.20 Поперечное сечение
потока
ис.3.20 Поперечное сечение
потока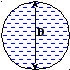


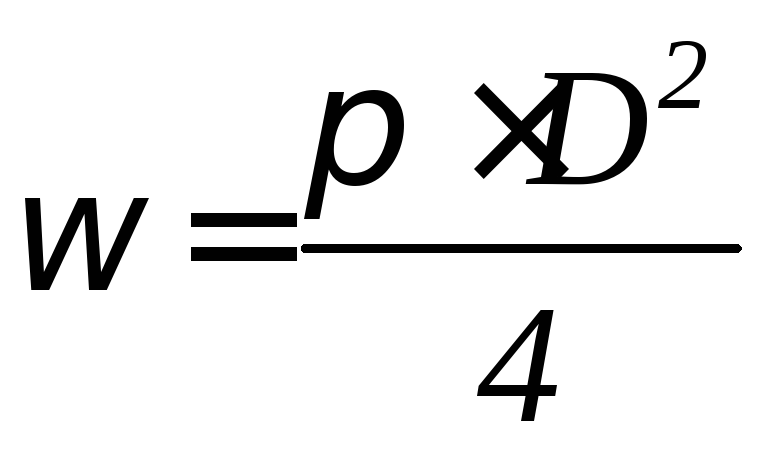 .
. .
.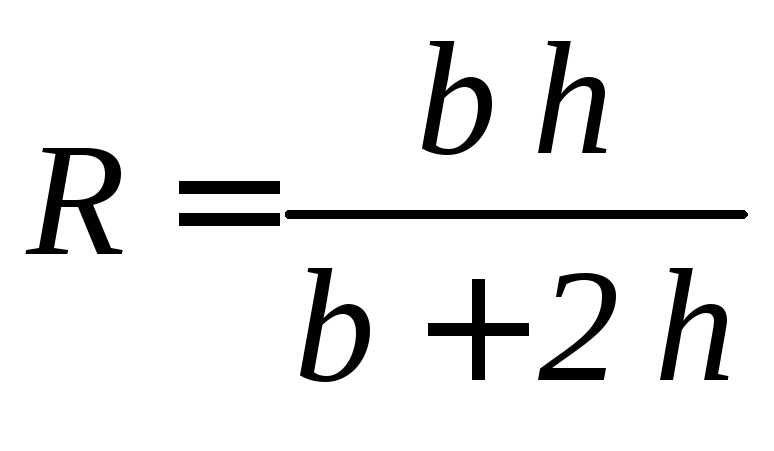 .
. .
.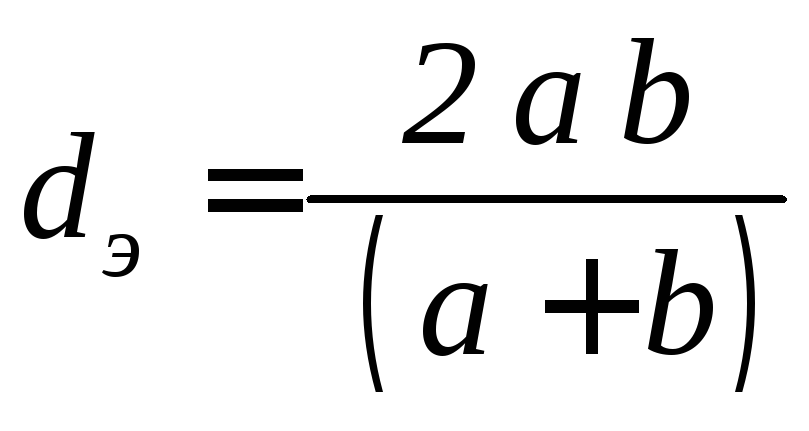 .
.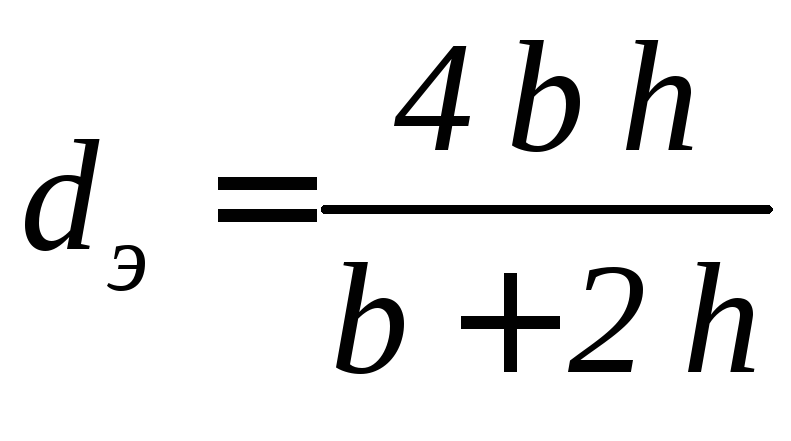 .
.