25,26,29. Центр параллельных сил. Центр тяжести твердого тела. Центр тяжести однородного объема, площади, материальной линии. Статический момент площади относительно оси.

Центр параллельных сил, точка, через которую проходит линия действия равнодействующей системы параллельных сил F_k при любом повороте всех этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол.

Координаты Центр параллельных сил определяются формулами: , , 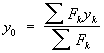где x_k, y_k, z_k - координаты точек приложения сил. Понятием Центр параллельных сил пользуются при отыскании координат центров тяжести тел. Центром тяжести тела называется точка, относительно которой суммарный момент сил тяжести, действующих на систему, равен нулю. 

Центр тяжести различных тел:

x_c = (∑ G_ix_i) / ∑ G_i;  y_c = (∑ G_iy_i) / ∑ G_i;  z_c = (∑ G_iz_i) / ∑ G_i.

центра тяжести фигуры, составленной из отрезков линий:

x_c = (∑ l_ix_i) / ∑ l_i;  y_c = (∑ l_iy_i) / ∑ l_i;  z_c = (∑ l_iz_i) / ∑ l_i.

центра тяжести фигуры, составленной из площадей:  x_c = (∑ F_ix_i) / ∑ F_i;  y_c = (∑ F_iy_i) / ∑ F_i;  z_c = (∑ F_iz_i) / ∑ F_i.

центра тяжести тела, составленного из однородных объемов:  x_c = (∑ V_ix_i) / ∑ V_i;  y_c = (∑ V_iy_i) / ∑ V_i;  z_c = (∑ V_iz_i) / ∑ V_i.

С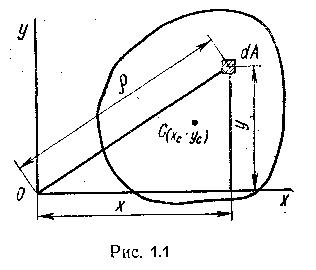татическим моментом Sx сечения относительно какой-либо оси х называется геометрическая характеристика, определяемая интегралом вида

  

где y - расстояние от элементарной площадки dA до оси x.

27. Методы нахождения центра тяжести (симметрии, разбиения, дополнения).

Метод интегрирования является универсальным. Он пригоден для определения координат центров тяжести однородных и неоднородных тел любой формы.

Метод разбиения – применяется, когда однородное тело можно разбить на части, положения центров тяжести которых известны или легко определяются. В неоднородном теле эти части должны иметь еще и одинаковый удельный вес во всех их точках. После разбиения положение центра тяжести всего тела находят, используя дискретные формулы для определения координат центра тяжести.

Метод симметрии применяется только для однородных тел.Сформулируем три правила метода.

1. имеет плоскость симметрии - центр тяжести лежит в этой плоскости.

2. имеет ось симметрии- центр тяжести находится на этой оси.

3. имеет центр симметрии- центр тяжести находится в этой точке.

Методы отрицательных весов, объемов и площадей являются частными случаями метода разбиений и применяются для тел с полостями (отверстия, вырезы и т.д.). В них используется идея метода разбиений, но при нахождении центра тяжести по формулам веса, объемы или площади полостей берут со знаком "-".

28. Центры тяжести дуги окружности и кругового сектора. Центр тяжести пирамиды.

Прямоугольник – центр тяжести на пересечении диагоналей.

Треугольник – центр тяжести на пересечении медиан.

Дуга окружности:

Круговой сектор

Полукруг:

Круговой сегмент: Для получения координаты необходимо разбивать сечение на круговой сектор и равнобедренный треугольник и затем применить метод отрицательных площадей.

Конус, пирамида: Центр тяжести находится от основания пирамиды на расстоянии равной ¼ высоты.