
- •2.Аксиомы статики
- •3. Связи и их реакции. Аксиома связей. Основные виды связей.
- •5. Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей.
- •11.Векторный момент силы относительно центра. Выражение векторного момента силы в виде векторного произведения. Аналитическое выражение момента силы относительно центра.
- •12. Момент силы относительно оси. Аналитическое выражение момента силы относительно оси.
- •13. Связь между моментом силы относительно оси и векторным моментом силы относительно точки.
- •9. Сложение параллельных сил.
- •9. Пара сил. Векторный момент пары сил. Алгебраический момент пары сил.
- •10. Свойства пар сил. Эквивалентность пар. Теоремы об эквивалентности пар.
- •10. Сложение пар сил. Условие равновесия системы пар сил.
- •15. Основная лемма статики о параллельном переносе силы.
- •16. Основная теорема статики о приведении системы сил к заданному центру (теорема Пуансо). Главный вектор и главный момент системы сил.
- •18. Инварианты приведения пространственной системы сил.
- •20. Уравнения равновесия плоской системы сил.( Три формы).
- •19. Статически определимые и неопределимые системы. Расчет составных конструкций.
- •30. Распределенные нагрузки.
- •22. Трение скольжения. Законы трения. Угол и конус трения. Условия равновесия тел на шероховатой поверхности.
- •23. Угол и конус трения. Условия равновесия тела на шероховатой поверхности
- •21. Расчет плоских ферм. Классификация ферм. Методы расчета плоских ферм. Леммы о нулевых стержнях.
- •25. Случаи приведения пространственной системы сил к простейшему виду.
- •17. Приведение системы сил к динаме. Уравнение центральной оси. Четыре случая приведения сил
- •20. Уравнение равновесия пространственной системы сил. Частные случаи.
- •25,26,29. Центр параллельных сил. Центр тяжести твердого тела. Центр тяжести однородного объема, площади, материальной линии. Статический момент площади относительно оси.
- •27. Методы нахождения центра тяжести (симметрии, разбиения, дополнения).
- •28. Центры тяжести дуги окружности и кругового сектора. Центр тяжести пирамиды.
- •31.Предмет кинематики. Пространство и время в классической механике. Относительность движения. Траектория движения точки. Основная задача кинематики.
- •33. Скорость точки при векторном способе задания движения.
- •34. Ускорение точки при векторном способе задания движения.
- •35. Скорость и ускорение при координатном способе задания движения.
- •36. Скорость точки при естественном способе задания движения.
- •37. Естественный трехгранник. Разложение ускорения по естественным осям. Касательное и нормальное ускорение.
- •37. Частные случаи движения точки. Смысл касательного и нормального ускорения.
- •39. Кинематика твердого тела. Виды движения твердого тела. Поступательное движение твердого тела.
- •40. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение вращательного движения тела. Угловая скорость и угловое ускорение.
- •41. Равномерное и равнопеременное вращение
- •42. Определение кинематических характеристик движения точек вращающегося тела. Траектории, закон движения. Скорость и ускорение точек вращающегося тела.
- •43. Выражение скорости и ускорения точки вращающегося тела в виде векторных произведений.
- •7. Теорема о трех силах
- •8. Расчет усилий в стержнях фермы методом вырезания узлов
- •38. Равномерное и равнопеременное движение точки
25. Случаи приведения пространственной системы сил к простейшему виду.
В зависимости от соотношения R0* и М0* возможны следующие случаи приведения:1) R0*=0 и М0*=0 – система сил находится в равновесии.2) R0*≠0 и М0*=0 – система сил приводится к равнодействующей, равной главному вектору, л.д. которой проходит через центр приведения (поступательное движение)
3) R0*=0 и М0*≠0 – система сил приводится к паре сил с моментом равным главному моменту с л.д. проходящей через центр приведения (вращательное движение)
4) R0*≠0 и М0*≠0 – система сил приводится к равнодействующей, равной главному вектору с л.д. проходящей через центр приведения (R0* перпендикулярно М0*) (плоско-параллельное движение)
5) R0*≠0 и М0*≠0 (R* параллельно М*) – система сил сводится к главному вектору и главному моменту с л.д. проходящими через центр приведения (винтовое движение)6) R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение)
Центр параллельных сил – точка, через которую проходит линия действия равнодействующей системы параллельных сил Fk при любом повороте всех этих сил около их точек приложения в одну и ту же сторону и на один и тот же угол.
17. Приведение системы сил к динаме. Уравнение центральной оси. Четыре случая приведения сил
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image001.gif"
\* MERGEFORMATINET
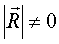 ;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image002.gif"
\* MERGEFORMATINET
;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image002.gif"
\* MERGEFORMATINET
![]() -
динама.
-
динама.
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image001.gif"
\* MERGEFORMATINET
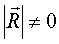 ;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image003.gif"
\* MERGEFORMATINET
;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image003.gif"
\* MERGEFORMATINET
![]() -
равнодействующая.
-
равнодействующая.
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image004.gif"
\* MERGEFORMATINET
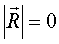 ;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image005.gif"
\* MERGEFORMATINET
;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image005.gif"
\* MERGEFORMATINET
![]() -
пара.
-
пара.
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image004.gif"
\* MERGEFORMATINET
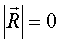 ;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image006.gif"
\* MERGEFORMATINET
;
INCLUDEPICTURE
"http://www.pppa.ru/metodika/theory/mechanics10.files/image006.gif"
\* MERGEFORMATINET
![]() -
равновесие.
-
равновесие.
Уравнения центральной винтовой оси Mx - yRz + zRy = pRx, My - zRx + xRz = pRy, Mz - xRy + yRx = pRz,
R0*≠0 и М0*≠0(R* перпенд М0*; R* парал М0*) – система сил сходится в динаме, ось которой не проходит через центр приведения (сложное движение)
20. Уравнение равновесия пространственной системы сил. Частные случаи.
Условия равновесия пространственной системы сил:

Шесть уравнений: три суммы проекций сил на оси координат и три суммы моментов относительно осей координат
Частные случаи:
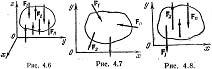 1)
Равновесие пространственной системы
параллельных сил.
1)
Равновесие пространственной системы
параллельных сил.
 Пусть
ось Z параллельна линиям действ силы,
тогда проекции сил на x и y равны 0 (Fkx=0
и Fky=0),
а остаётся только Foz.
А что касается моментов, то остаются
только Mox и
Moy,
а Mozотсутствует.
Пусть
ось Z параллельна линиям действ силы,
тогда проекции сил на x и y равны 0 (Fkx=0
и Fky=0),
а остаётся только Foz.
А что касается моментов, то остаются
только Mox и
Moy,
а Mozотсутствует.
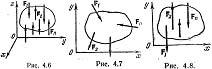
2) Равновесие плоской системы сил. Остаются ур-я Fox, Foy и момент Moz .
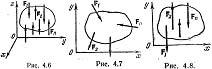 3)
Равновесие плоской системы параллельных
сил. Остаются только 2 ур-я: Foy и
Moz.При
составлении ур-ий равновесия за центр
привидения может быть выбрана любая
точка.
3)
Равновесие плоской системы параллельных
сил. Остаются только 2 ур-я: Foy и
Moz.При
составлении ур-ий равновесия за центр
привидения может быть выбрана любая
точка.
