39. Кинематика твердого тела. Виды движения твердого тела. Поступательное движение твердого тела.

Кинематика твёрдого тела — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

Виды движения твердого тела:

1) поступательное

2) вращательное

3) плоское или плоскопараллельное

4) сферическое

5) общий случай движения твердого тела

Поступательны движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе.

Теорема: Все точки твердого тела, движущегося поступательно, описывают одинаковые (совпадающие при наложении) траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.

40. Вращательное движение твердого тела вокруг неподвижной оси. Уравнение вращательного движения тела. Угловая скорость и угловое ускорение.

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения.

второй закон Ньютона для вращательного движения:

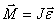
основного уравнения динамики вращательного движения:

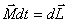
Углова́я ско́рость — векторнаявеличина, характеризующая скорость вращения тела.

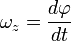
Углово́е ускоре́ние — псевдовекторнаяфизическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела.

,

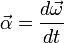41. Равномерное и равнопеременное вращение

Вращение называется равномерным, если в процессе движения угловая скорость остается постоянной по модулю и по направлению, то есть, если ω=const. Закон равномерного вращения: ρ=ρ0+ω*t.

Вращение называется равнопеременным, если угловое ускорение тела в процессе движения остается постоянным по модулю и направлению, т.е. ε=const. Закон изменения угловой скорости: ω=ω0+ε*t. Закон равнопеременного вращения: ρ=ρ0+ω0*t+ε*t2/2.

42. Определение кинематических характеристик движения точек вращающегося тела. Траектории, закон движения. Скорость и ускорение точек вращающегося тела.

Основные кинематические характеристики Вращательное движение тела — его угловая скорость ω и угловое ускорение ε. Для любой точки тела, отстоящей от оси на расстоянии h, линейная скорость v = hω, касательное ускорение w_τ = hω, нормальное ускорение w_n = hω² и полное ускорение 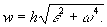 Закон вращения определяется из основного уравнения I_z ε = M_z,где M_z — вращающий момент

Модуль вращательной скорости точки твердого тела равен произведению расстояния от точки до оси вращения на угловую скорость тела.

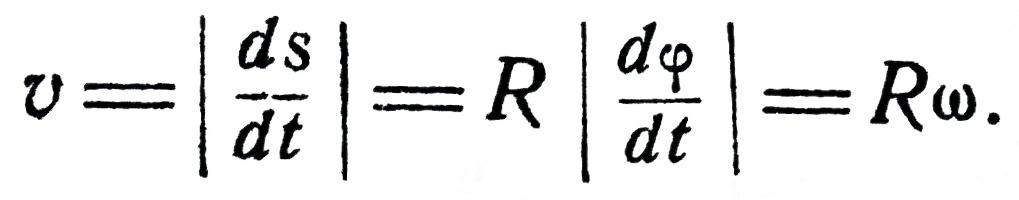
Модули вращательных скоростей различных точек вращающегося тела пропорциональны расстояниям от этих точек до оси вращения.

Модуль вращательного ускорения точки твердого тела равен произведению расстояния от точки до оси вращения на модуль углового ускорения тела.