36. Скорость точки при естественном способе задания движения.

а) траектория движения, т. е. линия в пространстве, с точками которой последовательно совмещается в своем движении исследуемая точка: с траекторией связана естественная система координат, показанная на рис. 3, где Q - соприкасающаяся плоскость, Т - касательная, N - главная нормаль и B - бинормаль к траектории в той ее точке, в которой находится движущаяся точка М в данный момент. 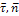 - орты осей Т и N;

б) начало 0 и направление (+, -) отсчета расстояний вдоль траектории;

в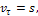) закон движения s=s(t), определяющий расстояние s от начала отсчета расстояний до положения точки в данный момент (дуговую координату точки).

Скорость точки определяется своей проекцией на касательную:

имеющий знак «+» в том случае, когда движение происходит в направлении отсчета расстояний.

37. Естественный трехгранник. Разложение ускорения по естественным осям. Касательное и нормальное ускорение.

Репер или трёхгранник Френе или Френе — Серре известный также, как естественный, сопровождающий, сопутствующий  — ортонормированный репер в трёхмерном пространстве, возникающий при изучении бирегулярных кривых.

Пусть γ(s) — произвольная натурально параметризованнаябирегулярная кривая в евклидовом пространстве. Под репером Френе понимают тройку векторов сопоставленную каждой точке бирегулярной кривой , где

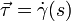• —единичный касательныйвектор,

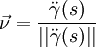• —единичный вектор главной нормали,

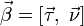• —единичный вектор бинормали

к кривой в данной точке.

Трёхгранник Френе играет важную роль в кинематике точки при описании её движения в «сопутствующих осях». Пусть материальная точка движется по произвольной бирегулярной кривой. Тогда, очевидно, скорость точки направлена по касательному вектору . Дифференцируя по времени находим выражение для ускорения: . Компоненту при векторе  называют тангенциальным ускорением, она характеризует изменение модуля скорости точки. Компоненту при векторе  называют нормальным ускорением. Она показывает, как меняется траектория движения точки.

Т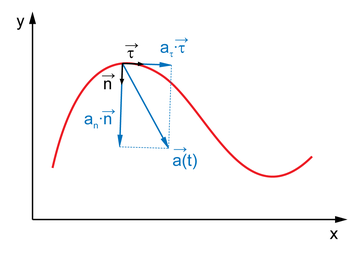ангенциа́льное ускоре́ние  — компонента ускорения, направленнаяпокасательной к траектории движения.

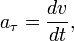
Центростремительное ускорение — часть полного ускорения точки, обусловленного кривизной траектории и скоростью движения по ней материальной точки.

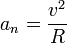
или

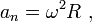
37. Частные случаи движения точки. Смысл касательного и нормального ускорения.

Частные случаи движения точки:

1) Прямолинейное:

радиус кривизны r= ¥(бесконечно большой) Þ а_n=0, a=a_t. 

2) Равномерное криволинейное движ-ие:

v=const Þ a_t=0, a=a_n. Ускорение появляется только за счет изменения направления скорости. Закон движ-ия: s=s₀+v×t, при s₀=0   v=s/t.

3) Равномерное прямолинейное движ-ие:

а=a_t=a_n=0. Единственное движение, где а=0.

4) Равнопеременное криволинейное движение:

 a_t=const, v=v₀+a_t×t,  . При равноускоренное движении знаки у a_t и v одинаковы, при равнозамедленном – разные.

Тангенциальное ускорение характеризует изменение модуля скорости точки.

Нормальное ускорение показывает, как меняется траектория движения точки.