Методичка по Математике

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусская государственная сельскохозяйственная академия

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

1) x y 2 z 1 0,

x y 2 z 3 0;

.pdf

Скачиваний:

171

Добавлен:

29.02.2016

Размер:

3.18 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

x x0 lt

y y0 mtz z0 nt

Ax By Cz D 0.

3) Подставим в четвертое уравнение системы правые части первых трех равенств, получим

A(x0 lt) B( y0 mt) C(z0 nt) D 0 .

Выразим из него значение параметра t:

t Ax0 By0 Cz0 D . Al Bm Cn

4. В результате подстановки значения параметра в правые части первых трех равенств получим координаты точки пересечения прямой и плоскости в пространстве:

x x0

Ax0 By0 Cz0 D

Al Bm

y y0

Ax0 By0

Cz0 D

Al Bm Cn

z z0

Ax0 By0 Cz0 D

Al Bm Cn

Пример 2. Известно, что прямая

x 2

y 4

z 5

и плоскость

x 2y z 1 0 пересекаются в точке Р.

Найти

координаты этой

точки.

Р еше н ие . Перейдём от канонических уравнений прямой к пара-

	x 2		y 4		z 5	x 2 3t
	x 2		y 4		z 5
метрическим:		t ,		t ,		t , или y 4 2t
метрическим:	3	t ,	2	t ,	2	t , или y 4 2t
	3		2		2
						z 5 2t.

Полученные выражения для x, y, z подставим в уравнение плоскости и найдём параметр t:

1-й способ:	2 3t 2( 4 2t) (5 2t) 1 0 ,			5t 12 0 , t	12			;
1-й способ:	2 3t 2( 4 2t) (5 2t) 1 0 ,			5t 12 0 , t		5		;
						5
2-й способ:	t	Ax0 By0 Cz0 D	1 2 2 ( 4) 1 5 1				12
									.
		Al Bm Cn		1 3 2 2 1 2				5	.
		83

Найденный параметр t подставим в параметрические уравнения плоскости и найдем координаты пересечения прямой и плоскости:

x 2 3	12	9	1	,	y 4 2					12					4	,	z 5 2	12	9	4	.
	5		5											5				5		5
											5
Таким образом, точка					P(9	1	;	4	; 9			4	)	пересечения прямой и плос-
						5		5			5

кости найдена.

4.24. Поверхности второго порядка

Поверхностью второго порядка называется геометрическое место

точек, координаты которых удовлетворяют уравнению вида

Ах2+ By2 +Cz2 +Dxy + Ехz + Fуz + Gx+Hy + Кz + L = 0,

где А, В, ..., L – действительные числа, причем, по крайней мере, один из коэффициентов А, В, С, D, E, F отличен от нуля.

Это уравнение называется общим уравнением поверхности второго порядка.

Поверхности второго порядка можно классифицировать на три основных типа: поверхности вращения, цилиндрические и конические поверхности.

Поверхности вращения

Поверхностью вращения вокруг оси d называется поверхность, каждое сечение которой, перпендикулярное оси d, является окружностью с центром, лежащим на этой оси.

Рассмотрим линию l, которая вместе с осью d лежит в плоскости L

(рис. 45).

z L

M l

(x, z)

Рис. 45

Будем вращать эту линию вокруг оси, при этом каждая точка линии опишет окружность, а вся линия l опишет поверхность вращения.

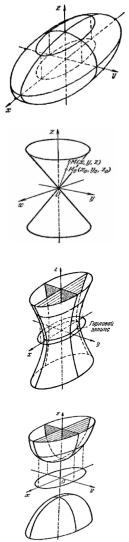
Если в качестве линии l вращать эллипс, то получится эллипсоид. Каноническое уравнение эллипсоида имеет вид

x2	y 2	z 2	1 .
a2	b2	c2

Числа а, b, с называются полуосями эллипсоида и представляют собой длины отрезков от начала координат до точек пересечения эллипсоида с осями координат.

Эллипсоид представляет собой ограниченную поверхность, симметричную относительно осей координат, которую можно заключить в параллелепипед (рис. 46).

Если вращать вокруг оси Oz пару прямых, пересекающихся в начале координат, то получим конус второго порядка (рис. 47).

Каноническое уравнение такой поверхности имеет вид


	x2			y 2		z 2		0 .
	a2			b2		c2

Однополостный гиперболоид – это поверх-
ность вращения гиперболы
		x	2		z2		1

		a	2		c2

вокруг оси Oz (рис. 48). Его каноническое уравнение –

Рис. 46

Рис. 47

Рис. 48


	x2			y2			z2	1.
	a2		b2				c2

Двуполостный гиперболоид – это поверхность
вращения гиперболы
		z2			x2		1

		c2				a2
вокруг оси Oz (рис.						49).		Его каноническое

Рис. 49

уравнение –

x2 y2 z2 1 . a2 b2 c2

Величины a, b, c называются полуосями соответствующих

поверхностей.
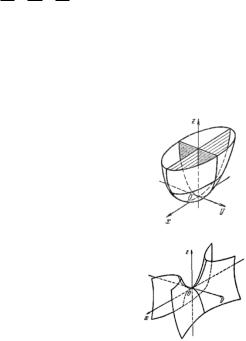
При вращении параболы							x2 2 pz вокруг её оси Oz получается
поверхность с уравнением
						x2 y2 2 pz ,
которую называют параболоидом вращения. Сжатие
к плоскости у=0 переводит параболоид вращения в
поверхность с уравнением
			x2		y2	2z .
			a2			2z .
			a2		b2
Поверхность (рис. 50), которая имеет такое
уравнение в некоторой декартовой прямоугольной
системе координат, называется эллиптическим								Рис. 50
системе координат, называется эллиптическим
параболоидом.
Простейшим		уравнением					гиперболического
параболоида (рис. 51) является
	x2	y2		2z ; (p>0,q>0).
				2z ; (p>0,q>0).
	p	q

Цилиндрические поверхности

Поверхность называется цилиндрической Рис. 51 поверхностью с образующей, параллельной оси Оz, если она обладает следующим свойством: какова бы ни была лежащая на этой поверхности точка М0(х0; у0, z), прямая линия, проходящая через эту точку и параллельная оси Оz, целиком лежит на данной поверхности.

Любая прямая, целиком лежащая на цилиндрической поверхности, называется образующей этой поверхности.

Аналогично определяются цилиндрические поверхности с образующими, параллельными осям Ох и Оу.

Можно доказать, что всякое уравнение вида

F(х, у) = 0

определяет цилиндрическую поверхность с образующей, параллельной оси Оz.

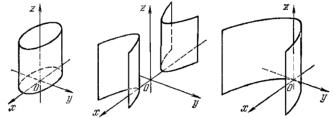
Например, уравнение x2+y2=R2 определяет круглый цилиндр с образующей прямой, параллельной оси Оz и направляющей, представляющей собой окружность, с центром в начале координат, лежащую в плоскости Оху.

В процессе классификации поверхностей второго порядка встречаются эллиптический, гиперболический и параболический цилиндры. Уравнения этих поверхностей соответственно имеют вид

x2	y2	1 ,	x2	y2	1 ,	y2 2 px .
a2	b2		a2	b2

Представление о форме этих цилиндров дает рис. 52.

Рис. 52

5. ЗАДАНИЯ, РЕКОМЕНДУЕМЫЕ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

ПО ТЕМЕ «АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПЛОСКОСТИ И ПРОСТРАНСТВЕ»

1. Определить,	какие из точек М1 (3; 1), M2 (2; 3), M3 (6; 3),
M4 ( 3; 3), M5 (3;	1), M6 ( 2; 1) лежат на прямой 2x 3y 3 0 , а

какие не лежат на ней. Построить данную прямую.

2. Точки P1 , P2 , P3 , P4 и P5 расположены на прямой 3x 2y 6 0 и

их абсциссы соответственно равны числам: 4, 0, 2, –2 и –6. Определить ординаты этих точек. Построить данную прямую.

3. Точки Q1 , Q2 , Q3 , Q4 и Q5 расположены на прямой x 3y 2 0

и их ординаты соответственно равны числам: 1, 0, 2, –1, 3. Определить абсциссы этих точек. Построить данную прямую.

4. Дана прямая 2x + 3y + 4 = 0. Составить уравнение прямой, проходящей через точку M0 (2; 1) : 1) параллельно данной прямой; 2) перпендикулярно к данной прямой. Построить эти прямые.

5. Найти проекцию точки P ( 6; 4) на прямую 4x 5y 3 0 .

6.	Даны	вершины	треугольника	A (5; 4), B( 1; 3), C( 3; 3) .
Составить уравнения его сторон и медиан.
7.	Даны	вершины	треугольника	M1 (2; 2),	M2 (3; 5), M3 (5; 7) .

Составить уравнения прямых, проходящих через вершины треугольника параллельно противоположным сторонам.

8. Даны прямые: 1) 2x 3y 6 0;			2) 4x 3y 24 0;
	3) 2x 3y 9 0; 4) 3x 5y 2 0.
Составить	для них	уравнения	«в отрезках» и	построить эти
прямые.
9. Найти	точку	пересечения	двух прямых	3x 4y 29 0 ,

2x 5y 19 0 .

10. Составить уравнение прямой, проходящей через точку М пересечения прямых x 2y 5 0 и 3x 2y 1 0 перпендикулярно к

прямой 2x 3y 7 0 .

11. Записать уравнение прямой, проходящей через точку M0 (2; 1) и составляющую с положительным направлением оси Оу угол 120 . Построить эту прямую.

12.Найти уравнение прямой, отсекающей на оси Оу отрезок b = –4

исоставляющей с осью Ох угол 45 .

13.Составить уравнение прямой и построить прямую на чертеже, зная ее угловой коэффициент k и отрезок b, отсекаемый ею на оси Оy:

1)	k	2		, b = 3;		2) k = 3, b = 0;	3) k = 0, b = –2;
		3

4)	k			3	, b = 3;	5) k = –2, b= –5;	6)	k	1	, b	2	.
			4						3		3

14.Определить угловой коэффициент k и отрезок b, отсекаемый на оси Оy, для каждой из прямых:

1) 5x–y+3=0; 2) 2x+3y–6=0; 3) 5x+3y+2=0; 4) 3x+2y=0; 5) y–3=0.

15.Вычислить угловой коэффициент k прямой, проходящей через две данные точки:

а) M1 (2; 5),	M2 (3; 2); б) P( 3;1), Q(7;8);		в) A(5; 3),	B( 1; 6) .
16. Определить угол между двумя прямыми:
1) 5x y 7 0 ,	3x 2y 0;	2) 3x 2y 7 0, 2x 3y 3 0 ;
		88

3)	x 2y 4 0,	2x 4y 3 0 ;			4) 3x 2y 1 0, 5x 2y 3 0 .
	17. Установить, какие из следующих пар прямых перпендику-
лярны:
	3x y 5 0;		3x 4 y 1 0;					6x 15y 7 0;
1)	x 3y 1 0.		2) 4x 3y 7 0.				3) 10x 4 y 3 0.
	9x 12 y 5 0;		7x 2 y 1 0;					5x 7 y 3 0;
4)	8x 6 y 13 0.		5) 4x 6 y 17 0.				6)	3x 2 y 5 0.
	18. Доказать, что в следующих случаях две данные прямые
параллельны:
	3x 5y 4 0;		2x 4 y 3 0;			2x 1 0;		2x y 1 0;
1)	6x 10 y 7 0.	2)	x 2 y	0.	3)	x 3 0.		4) 4x 2 y 7 0.

19. Дана прямая 5x + 3y – 3 = 0. Определить угловой коэффициент k прямой: 1) параллельной данной прямой; 2) перпендикулярной к данной прямой.

20. Даны вершины треугольника M (2; 1), N( 1; 1), P(3; 2) .

Составить уравнения его высот.

21. Вычислить расстояние d между параллельными прямыми в

каждом из следующих случаев:
a)	3x 4 y 10 0;	б)	5x 12 y 26 0;	в)	4x 3y 15 0;
	6x 8y 5 0.		5x 12 y 13 0.		8x 6 y 25 0.

22. Найти точку М1 , симметричную точке М2 (8; 9) относительно прямой, проходящей через точки A(3; 4) и B( 1; 2) .

23. Дан треугольник с вершинами в точках A(1;5) , B(2;0) , C(3;1) .

Составить уравнения стороны АС, высоты СК и медианы ВМ. Записать систему неравенств, определяющую внутренние точки треугольника.

24. Написать уравнение окружности радиуса R с центром в точке

а) R 3, M (0; 0) ;	б) R 4,	M ( 4; 1) .
25. Найти полуоси и фокусы эллипса.
10x2 6y2 60 ;	25x2 4y2 100 ;
4x2 9y2 36 ;		x2 10y2 10 .

Построить линии.

26. Найти полуоси и координаты фокусов гиперболы:

а)	x2		y2	1;	б)	y 2		x2	1;
а)				1;	б)				1;
4		9				9	4
					89


в)	4x2 y2 16;	г)	16x2 4y2 64. ;
д)	4x2 9y2 36;	е)	25x2 16y2 1;
Сделать построения.
27.	Написать уравнение параболы с вершиной в точке O 0; 0 и
параметром p , если
а) парабола направлена ветвями вправо и				p 2 ;
б) парабола направлена ветвями влево и				p 0,25;
в) парабола направлена ветвями вверх и				p 3.
28. Найти радиус и центр окружности
а) x2 y2 8x 6y 11 0 ;		б) 2x2 2y2 4x 8y 6 0 ;
в) 3x2 3y2 12y 0 ;		г) x2 y2 6x 7 0 .
29. Преобразовать заданные уравнения к каноническому виду и
построить соответствующие линии:
a) 5x2 9y2 30x 18y 9 0 ;		б) 5x2 2y2 50x 8y 27 0 ;
в) 16x2 9y2 64x 54y 161 0;		г) 9x2 16y2 90x 32y 367 0.
30. Построить линии, определяемые уравнениями

а) x 6 1 y2 ;		б) y 8 1 x2 ;

в) у 7 x ;		г) х 5 y .
31. Составить уравнение плоскости, которая проходит через точку
M1 (2; 1; 1) и перпендикулярна вектору n 1; 2; 3 .
32.	Даны две точки A(3; 1;	2)	и	B(4; 2; 1) . Составить

уравнение плоскости, проходящей через точку А перпендикулярно

вектору AB .

33. Составить уравнение плоскости, проходящей через точки M1 (2; 1; 3) и M2 (3; 1; 2) параллельно вектору a 3; 1; 4 .

34. Составить уравнение плоскости, проходящей через три точки

A(3; 1; 2) , B(4; 1; 1) и C(2; 0; 2) .

35. Определить двугранные углы, образованные пересечением следующих пар плоскостей:

3)6x 3y 2z 0, x 2y 6z 12 0;

4)x 2y 2z 3 0, 16x 12y 15z 1 0 .

36. Определить, при каких значениях l и m следующие пары уравнений будут определять параллельные плоскости:

1)2x ly 3z 5 0, mx 6y 6z 2 0 ;

2)3x y lz 9 0, 2x my 2z 3 0 ;

3) mx 3y 2z 1 0, 2x 5y lz 0 .

37. Определить, при каком значении l следующие пары уравнений будут определять перпендикулярные плоскости:

1) 3x 5y lz 3 0, x 3y 2z 5 0 ; 2) 5x y 3z 3 0, 2x ly 1 0 ;

3) 7x 2y z 0, lx y 3z 1 0 .

38. Составить уравнение плоскости, которая проходит через начало координат параллельно плоскости 5x 3y 2z 3 0 .

39. Составить уравнение плоскости, которая проходит:

1)через ось Ох и точку M1 (4; 1; 2) ;

2)через ось Оу и точку M2 (1; 4; 3) ;

3)через ось Оz и точку M3 (3; 4; 7) .

40. Найти точки пересечения плоскости 2x 3y 4z 24 0 с осями

координат.

41. Дано уравнение плоскости x 2y 3z 6 0 . Написать для нее

уравнение «в отрезках». Построить эту плоскость.

42. Вычислить расстояние d от точки до плоскости в каждом из следующих случаев:

1)M1 ( 2; 4; 3), 2x y 2z 3 0;

2)M2 (2; 1; 1), 16x 12y 15z 4 0;

3) M3 (3; 6;7),

4x 3z 1 0.

43. В каждом из следующих случаев вычислить расстояние между параллельными плоскостями:

1)	x 2 y 2z 12 0,	2)	2x 3y 6z 14 0,
	x 2 y 2z 6 0;		4x 6 y 12z 21 0;

44. Составить канонические уравнения прямой, проходящей через точку M 1(2; 0; 3) параллельно:

1) вектору a 2; 2; 5 ; 2) прямой	x 1		y 2	z 1	; 3) оси Ох;
1) вектору a 2; 2; 5 ; 2) прямой				1	; 3) оси Ох;
	5	2		1
4) оси Оу; 5) оси Оz.

45. Составить канонические и параметрические уравнения прямой, проходящей через точки A(1; 2; 1), B(3; 1; 1). Определить координа-

ты направляющего вектора этой прямой.

46. Даны вершины треугольника

A(1; 3; 2) ,

B(4; 1; 0) , C(3; 3; 2) .

Составить уравнение медианы СМ.

47.

Найти

острый угол между

прямыми:

x 3

y 2

x 2

y 3

z 5

48. Доказать:

x 2

y 1

x y z 0

параллельность прямых

;

y 5z 8 0

x 2t 1

2x y 4z 2

2) перпендикулярность прямых y 3t 2 и

y 5z 4

6t 1

49.

Даны

точки A(2; 3; 4) ,

B(1; 0; 6) ,

C( 3; 1; 5) . Составить

канонические уравнения прямой, проходящей через точку А параллельно отрезку ВС.

50.Составить канонические и параметрические уравнения прямой, проходящей через точку M(2; 4; 1) параллельно оси Oz.

51.Составить канонические уравнения прямой, проходящей через

точку A(2; 1; 4) параллельно прямой x 2 3t , y 1 t , z 5t .

52. Составить канонические и параметрические уравнения следующих прямых:

		x 2 y 3z 4 0		2x 3y z 4 0			5x y z 0
1)			2)		0;	3)		0.
	3x 2 y 5z 4 0;			3x 5y 2z 1	0;		2x 3y 2z 5	0.

53. Составить канонические уравнения прямой, проходящей через

точку M0 (3; 4; 2) параллельно прямой	7x y z 8 0
точку M0 (3; 4; 2) параллельно прямой
	6x y 2z 7	0.
92

<<< < Предыдущая 1 2 3 4 5 6 7 89 / 109 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
29.02.2016668.16 Кб79методичка межхоз.doc
#
29.02.2016171.82 Кб161методичка по анализу ФО.docx
#
29.02.2016327.52 Кб22методичка по к.р..pdf
#
29.02.2016143.41 Кб33методичка по курсовой работе Мониторинг.docx
#
29.02.201670.14 Кб14Методичка по курсовым работам по ТТТД.doc
#
29.02.20163.18 Mб171Методичка по Математике.pdf
#
15.08.2019207.36 Кб8Методичка по ОУИС.DOC
#
29.02.2016773.63 Кб16методичка по СП.doc
#
29.02.2016667.53 Кб104методичка по физиологии Усова.pdf
#
29.02.2016454.66 Кб59методичка по философии.doc
#
29.02.2016450.05 Кб52методичка по философии.doc