
Методичка по Математике
.pdfЛегко показать, что , где А – квадратная матрица, Е – единичная матрица того же размера.
1 |
2 |
1 |
и |
1 |
3 |
произведение |
|||
Например, для матриц |
|
|
|
|
|
|
|
||
|
3 |
1 |
0 |
|
|
|
2 |
|
|
|
|
|
1 |
|
|
||||
не определено, так как число столбцов матрицы А равно трем.
Оно не совпадает с числом строк матрицы В, равным двум, но при этом определено произведение , которое вычисляют следующим
образом: |
|
|
|
|
|
|
|
|
|
|
|
1 3 |
1 2 |
1 |
|
1 9 |
2 3 1 0 |
10 |
5 1 |
||||
|
|
|
|
|
|
6 |
2 2 1 0 |
|
|
|
. |
1 2 |
|
3 1 |
0 |
|
1 |
|
|
7 |
4 1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Если для заданных матриц операция умножения определена, то
справедливы следующие свойства: |
|
|
|
||||||
|
1) C C; |
|
|
2) С С; |
|||||
|
3) . |
|
|
|
|
|
|||
|
|
|
|
|
|
3 |
2 |
|
|
|
П ри м е р 2 . Дана матрица А= |
. Найти А3. |
|
||||||
|
|
|
|
|
|
1 |
4 |
|
|
|
Р еше н ие . Найдем квадрат матрицы A, т. е. произведение А А: |
||||||||
|
|
|
А2 |
|
|
3 2 |
3 2 |
11 14 |
|
|
|
|
=А А= |
|
|
= |
. |
||
|
|
|
|
|
|
1 4 |
1 4 |
7 18 |
|
|
Найдем куб матрицы A3, для этого перемножим A на A2, получим |
||||||||
3 |
3 |
2 11 14 |
|
47 |
78 |
|
|
|
|
A = |
|
= |
|
. |
|
|
|
||
|
1 |
4 7 18 |
|
39 |
86 |
|
|
|
|
2.2. Определители второго и третьего порядка, их свойства и вычисление
Квадратной матрице А порядка n можно поставить в соответствие
число |
A |
(det(A)), называемое ее |
определителем, по |
следующим |
|||||||||||||||||||
правилам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– если n=1, т. е. A (a11 ), |
то |
|
A |
|
a11; |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
– если n=2, т. е. |
a |
a |
|
|
A |
|
|
|
a |
a |
|
a |
a |
|
a |
a |
|
. |
|||||
|
|
|
|
|
|
||||||||||||||||||
A 11 |
12 |
, то |
|
|
|
11 |
12 |
|
22 |
21 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a21 |
a22 |
|
11 |
|
12 |
|
|
|||||
|
|
|
a21 |
a22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
П ри м е р 1 . Найти определители матриц |
2 3 |
|
||||
|
. |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
5 6 |
|
Р еше н ие . |
|
3 |
|
2 6 5 3 12 15 |
27 . |
|
2 |
|
|||||
|
5 |
6 |
|
|
|
|
Для того чтобы обобщить методику вычисления определителей квадратных матриц, введем понятие минора и алгебраического дополнения.
Минором Mij выбранного элемента aij матрицы n-го порядка
называется определитель п–1-го порядка, полученный из исходной матрицы путем вычеркивания в ней строки и столбца, на пересечении которых находится этот элемент.
Например, если исходной матрицей является матрица 3-го порядка
a |
a |
a |
|
|
|
|
|
|
|
|
|
|
11 |
12 |
13 |
|
|
a22 |
a23 |
|
|
|
a11 |
a13 |
|
a21 |
a22 |
a23 |
, то M11 |
, а M32 |
. |
|||||||
|
|
|
|
|
a32 |
a33 |
|
|
|
a21 |
a23 |
|
a31 |
a32 |
a33 |
|
|
|
|
|
|
|
|
|
|
Алгебраическим дополнением ij |
элемента aij |
квадратной матрицы |
||||||||||
называется ее минор, взятый со знаком плюс, если сумма индексов выбранного элемента i j – четное число, и со знаком минус, если эта
сумма нечетная, т. е. ij 1 i j Mij .
Например, для матрицы 3-го порядка 11 M11, 32 M32 . Прим ер 2 . Выписать минор М22 и алгебраическое дополнение А23
1 |
3 |
4 |
|
|
|
2 |
0 |
11 |
|
для заданной матрицы |
. |
|||
|
6 |
4 |
5 |
|
|
|
|||
Р еше н ие . Для получения минора М22 исключим из матрицы
вторую строку и второй столбец. Получаем М22= |
1 |
4 |
29 . |
|
6 |
5 |
|
Для записи алгебраического дополнения А23 |
исключаем из данной |
||
матрицы вторую строку, третий столбец. Учтем местоположение элемента a23 с помощью коэффициента (–1)2+3 = (–1)5= –1. В результате
алгебраическое дополнение А23 запишется в виде А23= |
|
3 |
|
22 . |
1 |
|
|||
|
6 |
4 |
|
|
Ответ: М22= – 29, А23= – 22.
14
Определитель матрицы n-го порядка при n>2 вычисляется на основе разложения его по элементам некоторого ряда, т. е. равен сумме произведений элементов некоторого ряда заданной квадратной матрицы на соответствующие им алгебраические дополнения. При этом схемы разложений определителя по выбранной к-й строке или выбранному p-му столбцу будут выглядеть соответственно:
a11 |
a12 |
... |
a1n |
|
|
|
|
|
|
n |
n |
a21 |
a22 |
... |
a2n |
akj Akj aip Aip ; |
|
... ... ... ... |
j 1 |
i 1 |
|||
|
|
|
|
||
an1 |
an2 |
... |
ann |
|
|
где akj и aip – элементы выбранного ряда;
Akj и Aip – алгебраические дополнения соответствующим элементам выбранного ряда матрицы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
||
П ри м е р 3 . Вычислить определитель матрицы |
3 |
1 |
4 |
. |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0 |
3 |
|
|
2 |
1 |
|
3 |
4 |
|
5 |
1 |
|
|
|
|
|
|||||
|
5 |
|
|
|
|
|
|
|
||||||||||
Р еше н ие . |
|
A |
|
|
3 |
1 |
4 |
( 2) |
1 |
|
|
|
|
|||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
6 |
0 |
3 |
|
6 |
3 |
|
6 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 ( 9 24) 1 ( 15 6) |
2 15 21 9 . |
|
|
|
|
|
|
|
|
|
||||||||
Определители матриц обладают приведенными ниже свойствами:
1)определитель не изменится, если строки определителя заменить столбцами, а столбцы – соответствующими строками;
2)общий множитель элементов любой строки (или столбца) может быть вынесен за знак определителя;
3)если элементы одной строки (столбца) определителя соответственно равны элементам другой строки (столбца), то определитель равен нулю;
4)при перестановке двух строк (столбцов) определитель меняет знак на противоположный;
5)определитель не изменится, если к элементам одной строки (столбца) прибавить соответственно элементы другой строки (столбца), умноженные на одно и то же число.
15

2.3. Системы линейных уравнений, основные понятия
Системой линейных алгебраических уравнений, содержащей m
уравнений и n неизвестных, называется система вида
a x a x |
|
a |
x |
|
|
b |
|
||||||
11 1 |
12 |
2 |
|
1n |
|
n |
|
1 |
|
||||
a21x1 a22 x2 a2n xn |
b2 |
, |
|||||||||||
.................................................. |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x a |
m2 |
x |
2 |
a |
mn |
x |
n |
b |
|
|||
|
m1 1 |
|
|
|
|
m |
|
||||||
где aij – коэффициенты системы; bi – свободные члены системы;
x1, x2 ,...,xn – неизвестные системы;
i 1,m ; j 1,n .
Если ввести следующие обозначения:
a
11
a21
am1
a |
a |
|
12 |
1n |
|
a22 |
a2n |
– матрица коэффициентов; |
|
|
|
|
|
|
|
|
|
am2 |
|
|
amn |
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
x2 |
|
– вектор-столбец из неизвестных x j ; |
|
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
1 |
|
|
|
|
b |
b2 |
|
– вектор-столбец из свободных членов |
b |
, |
|
|
|
|
||||
|
|
|
i |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
bm |
|
|
|
||
то система линейных уравнений записывается в матричной форме
A х=b.
Решением системы называется n значений неизвестных x1 c1, x2 c2 , , xn cn , подстановка которых в уравнения системы обращаeт их в тождества. Всякое решение системы можно записать в
16
виде матрицы-столбца элементами которого являются значения с1,
с2,…, сn.
Система уравнений называется совместной, если имеет хотя бы одно решение, и несовместной, если не имеет ни одного решения. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если имеет более одного решения. В случае неопределенной системы каждое ее решение называется частным решением. Совокупность всех частных решений системы называется ее общим решением.
Решить систему – это значит выяснить, совместна она или несовместна. В случае совместности системы находится ее общее решение.
Две системы называются эквивалентными (равносильными), если они имеют одно и то же общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой и наоборот. Эквивалентные системы получаются, в частности,
при элементарных преобразованиях системы при условии, что пре-
образования выполняются лишь над строками матрицы.
Система линейных уравнений называется однородной, если все свободные члены равны нулю:
a x a x |
|
a |
x |
|
|
0 |
|||||
11 1 12 |
2 |
|
1n |
|
n |
|
|
||||
................................................ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
x a |
m2 |
x |
2 |
a |
mn |
x |
n |
0. |
||
|
m1 1 |
|
|
|
|
||||||
Однородная система всегда совместна, так как x1 x2 xn 0 является решением системы. Это решение называется нулевым.
2.4. Решение систем линейных уравнений методом Крамера.
Пусть дана система n линейных уравнений с n неизвестными, т. е.
квадратная система
a x a x |
|
|
a |
|
|
x |
|
|
b |
|
|||||
11 1 |
12 |
|
2 |
|
n1 |
|
|
n |
1 |
|
|||||
a21 x1 a22 x2 |
a2n xn |
b2 |
, |
||||||||||||
.................................................. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
x a |
n2 |
x |
2 |
a |
nn |
x |
n |
b |
|
|||||
|
n1 1 |
|
|
|
|
|
|
|
n |
|
|||||
или в матричной форме A х=b. Определитель этой матрицы
17

|
a11 |
an1 |
|
|
|
|
an1 |
ann |
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.
Правило Крамера решения системы n линейных уравнений с n неизвестными можно сформулировать так:
– если определитель системы не равен нулю ( 0), то система
|
i |
|
|
|
|
|
имеет единственное решение, причем x |
, |
i 1, n ; |
||||
|
||||||
i |
|
|
|
|
||
|
|
|
|
|||
– если определитель системы равен нулю ( =0) и все i=0, i 1, n , то система имеет бесчисленное множество решений;
– если определитель системы равен нулю ( =0) и найдется такое к, что к 0, то система является несовместной, т. е. не имеет ни одного решения.
П ри м е р 1 . Решить систему |
2x1 x2 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 3x2 |
7. |
|
|
|
|
|
|
Р еше н ие . Найдем определитель системы |
|
|
1 |
|
7 0. |
Так |
||
2 |
|
|||||||
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
как он не равен нулю, то можем сделать вывод, что система имеет
|
i |
|
|
|
|
|
единственное решение, причем x |
, |
i 1, 2 . |
||||
|
||||||
i |
|
|
|
|
||
|
|
|
|
|||
Вычислим вспомогательные определители: |
||||||
|
1 |
|
7, |
|
|
2 |
0 |
|
|
|
0 |
|
2 |
|
14 . |
||||
1 |
7 |
3 |
|
|
|
1 |
7 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Тогда x1 77 1, x2 147 2.
2x 3y 1
Прим ер 2 . Решить систему линейных уравнений
4x 6 y 2.
методом Крамера.
Р еше н ие . Вычислим определители системы:
|
|
2 3 |
|
12 12 0; |
|
|
1 3 |
|
6 6 0; |
|
|
|
|
||||||
|
|
4 6 |
|
|
1 |
|
2 6 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
18 |
|
|
|

21
2 4 2 4 4 0 .
Так как все определители 1 2 0 , то данная система урав-
нений является неопределенной. Найдем множество решений системы, придавая одной из переменных произвольные значения. Пусть x R , тогда выражаем переменную y через х, например, из первого
уравнения: |
3y 2x 1 y |
2x 1 |
. Итак, |
множество |
системы |
|||||||||||
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
уравнений имеет вид x R; y |
|
2x 1 |
|
2x 1 |
|
|||||||||||
|
|
|
|
|
|
или x; |
|
. |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
y 4 |
При м е р 3 . Решить систему линейных уравнений |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9x 3y 1. |
|
методом Крамера. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Р еше н ие . Вычислим определители системы: |
|
|||||||||||||||
|
|
1 |
|
9 9 0; |
|
|
4 |
1 |
|
12 1 11; |
|
|||||
3 |
|
|
|
|
||||||||||||
|
9 |
3 |
|
|
1 |
|
1 |
3 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
34
2 9 1 3 36 33 .
Так как определитель системы 0 , а вспомогательные определи-
тели 1 |
11 0; |
2 |
33 0 , то система уравнений несовместна или |
||||
имеет решений |
|
|
|||||
Прим ер 4 . Найти решение системы уравнений |
|||||||
|
|
|
|
|
|
|
5x y z 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 y 3z 14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x 3y 2z 16. |
Р еше н ие . Вычислим определители системы: |
|||||||
|
1 |
1 |
|
|
|
|
|
|
5 |
|
|
|
|||
= |
1 |
2 |
3 |
|
= 5(4 – 9) + (2 – 12) – (3 – 8) = –25 – 10 + 5 = –30; |
||
|
4 |
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
19

|
|
|
|
1 |
1 |
|
|
||||
|
|
0 |
|
||||||||
1= |
14 |
2 |
|
3 |
|
|
= (28 – 48) – (42 – 32) = –20 – 10 = –30; |
||||
|
|
16 |
3 |
|
2 |
|
|
|
|||
|
|
0 |
1 |
|
|
|
|
|
|||
|
|
5 |
|
|
|
||||||
2= |
|
1 |
14 |
3 |
|
|
|
|
|
= 5(28 – 48) – (16 – 56) = –100 + 40 = –60; |
|
|
|
4 |
16 |
2 |
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|||||
|
5 |
|
|
|
|
||||||
3 = |
1 |
2 |
14 |
|
= 5( 32 – 42) + (16 – 56) = –50 – 40 = –90. |
||||||
|
4 |
3 |
16 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Значит, система имеет единственное решение x1= 1/ =1; x2= 2/ =2; x3= 3/ =3.
2.5. Векторы, основные понятия
Вектором называется направленный отрезок. Вектор с началом в
точке А и концом в точке В обозначается символом AB (или a ,
b , …).
Модулем (длиной) вектора AB называется расстояние от начальной
точки А до конечной точки В вектора и обозначается AB , à .
Единичным (или ортом) называется вектор |
|
которого |
|||
e , длина |
|||||
равна единице. |
|
|
|
|
|
|
|
|
|
||
Нулевым (или нуль-вектором) называется |
вектор |
0 , длина |
|||
которого равна нулю. |
|
|
|
|
|
Коллинеарными называются векторы |
если они лежат на |
||||
a |
и b , |
||||
|
|
|
|
|
|
одной прямой или на параллельных прямых; записывают a | |b .
Компланарными называются три вектора и более, если они лежат в
одной плоскости или в параллельных плоскостях. |
|
|
|
|
|
|
|
Равными ( a |
b ) называются два коллинеарных вектора |
a |
и b , |
если они одинаково направлены и имеют равные длины.
Всякие векторы можно привести к общему началу, т. е. построить векторы, соответственно равные данным и имеющие общее начало. Из
20
определения равенства векторов следует, что любой вектор a имеет бесконечно много векторов, равных ему.
Углом |
между |
векторами |
|
|
называется |
|
|
|
|
|
|||||
a |
и b |
|
|
|
|
|
|||||||||
наименьший угол |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(a |
ˆ; b) , на который нужно |
|
|
|
a |
|
|||||||||
повернуть вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|||
a , чтобы его направление совпало |
|
A |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
с направлением вектора |
b , |
при |
условии, |
что оба |
|
|
|
b |
|
||||||
вектора отнесены к общему началу, (рис. 1). |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||
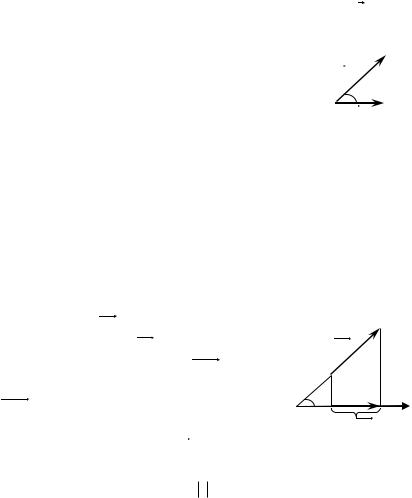
Угол |
между векторами |
измеряется |
в пределах |
|
|
|
Рис. 1 |
||||||||
|
|
|
|
|
|||||||||||
0 |
ˆ |
. Если угол между векторами |
|
|
|
(или 90 ), то |
|||||||||
(a ; b) |
(a |
ˆ; b) |
2 |
|
|||||||||||
векторы называются ортогональными. В случае, когда |
|
|
0 (или |
||||||||||||
(a |
ˆ; b) |
||||||||||||||
0 ), |
говорят, что |
вектор |
|
сонаправлен |
с вектором |
|
|
||||||||
a |
b , если же |
||||||||||||||
ˆ |
|
(или |
180 ), |
то |
вектор |
|
имеет противоположное |
||||||||
(a ; b) |
a |
||||||||||||||
направление к вектору b .
2.6. Координаты вектора и его длина
Пусть вектор AB составляет угол с осью l . Проекцией вектора AB на ось l называется число, равное длине вектора A1B1 (рис. 2), взятое со знаком плюс, если направление вектора A1B1 совпадает с направлением оси l , и со
знаком минус в противном случае.
Проекция вектора a AB на ось l вычисляется по формуле
прl а а сos( ) .
|
B |
AB |
|
A |
|
A |
B1 |
1 |
|
прl AB |
l |
|
|
Рис. 2 |
|
Декартовыми прямоугольными координатами x, y, z вектора a
называются его проекции на соответствующие координатные оси
Ox,Oy,Oz .
Вектор a с координатами x, y, z записывают в координатной
|
|
|
|
|
форме a(x; y; z) или в виде разложения по базису |
a |
xi |
yj |
zk , где |
21 |
|
|
|
|

i, j, k – орты координатных осей Ox,Oy,Oz соответственно (или
базисные векторы).
Длина вектора a определяется по формуле
|
|
|
|
|
|
x2 y2 z2 . |
|
|
|
|
|
|
|
||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||||
|
|
2.7. Действия над векторами и их свойства |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Суммой двух |
векторов |
b |
называется |
|
|
|
|
|
|
||||||||
a и |
|
|
|
|
a |
|
|||||||||||
|
|
соединяющий |
начало |
вектора |
|
|
|
|
|
||||||||
вектор c , |
a с |
|
a |
|
b |
|
|
b |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
концом вектора |
b , при условии, что вектор b |
|
|
|
|
|
|
|
|||||||||
отложен от конца вектора |
|
(рис. 3). |
|
|
|
|
|
|
|
|
|||||||
a |
|
|
|
|
|
|
a b |
||||||||||
Произведением вектора |
|
на число |
0 |
|
|
|
|
|
|
|
|||||||
a 0 |
|
|
|
Рис. 3 |
|
|
|||||||||||
называется вектор, который имеет длину |
|
|
|
|
|
|
|
|
|
||||||||
a и |
|
|
|
|
|
|
|
||||||||||
коллинеарен вектору |
|
Причем векторы |
|
a |
сонаправлены в |
||||||||||||
a . |
a и |
||||||||||||||||
случае 0 и имеют противоположные направления, |
если 0 . |
|
|||||||||||||||
Пример |
1 . |
Даны |
векторы |
|
и |
|
|
|
|
|
|
|
|
||||
a |
b . |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
||
Построить вектор 3a |
2 b . |
|
|
|
|
|
|
|
|
2 b |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
3a |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
3a |
2 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2 . Векторы a и b образуют угол |
|
|
|
|
|
C |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
60 , |
|
|
a 2 , |
b 7 . |
|
|
|
|
|
B |
b |
|
|
||||
причем |
Определить |
|
|
|
|
|
|||||||||||
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a |
60 a |
b |
|
|
|
|
a b и |
a b . |
|
|
|
|
|
|
|
|
A |
|
|
D |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Р еше н ие . Суммой векторов |
a и b является вектор |
AC a b . |
|||||||||||||||
Заметим, что ABC = 120 . Тогда длину вектора |
AC можем найти по |
||||||||||||||||
теореме косинусов
AC a b 

 a 2 b 2 2 a
a 2 b 2 2 a
 b cos( ABC)
b cos( ABC)
22
