
Методичка по Математике
.pdf
Пример. |
Найти |
|
расстояние |
от |
точки |
|
M0 (2; 1) |
до |
прямой |
|||||||||||
4x 3y 10 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Р еше н ие . Воспользуемся расчетной формулой |
|
|
|
|
|
|
|
|||||||||||||
d |
Ax0 By0 C |
|
4 2 ( 3) 1 10 |
|
8 3 10 |
|
15 |
3 (ед. дл.). |
||||||||||||
A2 B2 |
42 ( 3)2 |
16 |
|
9 |
5 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
4.13. Эллипс, его канонические уравнения |
|
|
|
|||||||||||||||
Эллипсом называется линия, состоящая из всех точек плоскости, |
||||||||||||||||||||
для каждой из которых сумма расстояний до двух данных точек F1 и |
||||||||||||||||||||
F2, называемых фокусами эллипса, есть величина постоянная, равная |
||||||||||||||||||||
2а, большая, чем расстояние 2с между фокусами. |
|
|
|
|
|
|
|
|||||||||||||
Величину а для эллипса называют большей полуосью, а с – |
||||||||||||||||||||
полуфокусным расстоянием. Очевидно, что большая полуось эллипса |
||||||||||||||||||||
с его полуфокусным расстоянием связаны соотношением а > c. |
|
|
||||||||||||||||||
|
|
y |
|
|
|
|
|
|
|
Уравнения эллипса, |
фокусы |
|||||||||
|
|
|
M(x; y) |
|
|
которого |
располагаются |
сим- |
||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
метрично |
относительно |
|
начала |
||||||||
|
|
|
|
|
|
|
|
|
координат и лежат на одной из |
|||||||||||
|
|
O |
|
|
|
|
|
|
осей называется каноническими |
|||||||||||
|
F1 |
|
|
|
F2 |
x |
уравнениями. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
Каноническое уравнение эл- |
||||||||||
|
|
|
2c |
|
|
|
|
|
липса |
(рис. |
|
25) |
|
с |
фокусами, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2a |
|
|
|
|
|
расположенными |
|
симметрично |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 25 |
|
|
|
|
относительно начала координат |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
на оси Ох имеет вид |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|||||
|
|
x2 |
y2 |
|
|
|
|
|
|
|
|
|
|
M(x; y) |
||||||
|
|
1, |
|
|
|
|
|
|
|
F2 |
|
|
||||||||
|
|
a |
2 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
b2= a2 c2 |
0 , |
(b≤a, b |
– |
малая |
|
|
|
|
|
|
|
|
|
|
|||||
полуось эллипса). |
|
|
|
|
|
|
2a |
|
|
|
|
|
|
|
|
2c |
||||
Аналогичное уравнение |
|
|
|
|
|
|
O |
|
|
|
x |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x2 y2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
b2 |
a2 |
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|||
имеет эллипс (рис. 26) с фокусами, |
|
|
|
|
|
|
|
|
|
|
||||||||||
расположенными симметрично относи- |
|
|
|
|
2b |
|
|
|
|
|||||||||||
тельно начала координат на оси Оу. |
|
|
|
|
|
Рис. 26 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
53 |
|
|
|
|
|
|
|
|
|
|
|
|
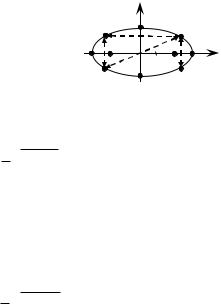
Исследуем форму эллипса (рис. 25).
1.Канонические уравнения эллипса содержат переменные х и у в четных степенях, поэтому любая точка эллипса будет иметь на нем симметричные точки относительно осей координат и начала координат. При этом начало координат называют центром эллипса.
2.Найдем точки пересечения эллипса с осями координат.
Точками пересечения эллипса с |
осью |
|
|
y |
|
|
Ох являются точки A1(–a; 0) и A2(a; 0). |
|
|
|
|
||
M1(–x; y) |
|
|
B2 |
|
||
Эллипс имеет также две точки пересечения |
|
|
M(x; y) |
|||
|
|
|
|
|||
с осью Оу – В1(0; –b) и В2(0; b). |
|
F1 |
|
|
|
|
Точки А1, А2, В1, В2 (рис. |
27) |
А1 |
|
O |
|
F2 А2 x |
называются вершинами эллипса, а отрезки |
M2(x; –y) |
|
|
|
M2(x; –y) |
|
А1А2 и В1В2 – соответственно большой и |
|
|
B1 |
|||
|
|
|
|
|||
малой осями эллипса. |
|
|
|
Рис. 27 |
||
3. Разрешим рассматриваемое |
|
|
|
|
|
|
уравнение относительно переменной у. В результате получим y ba 
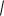 a2 x2 .
a2 x2 .
Знаки правой части данных равенств характеризуют фрагменты графика эллипса, на которые он разбивается осью Ох. Знак «+» соответствует фрагменту графика эллипса, лежащему над осью Ох, а «–» – под этой осью. Равенства определены для значений переменной х, изменяющихся в пределах –а ≤ х ≤ а.
Разрешим рассматриваемое уравнение относительно переменной х, получим
x ba 
 b2 y2 .
b2 y2 .
Знак «+» будет соответствовать фрагменту графика эллипса, лежащему правее оси Оу, а «–» – левее этой оси. Равенство определено для значений переменной y, изменяющихся в пределах –b ≤ y ≤ b.
Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми х = а, y = b.
4. В рассматриваемом уравнении сумма неотрицательных слага-
|
x2 |
|
y2 |
|
емых |
|
и |
|
равна единице. Следовательно, при возрастании одного |
a2 |
b2 |
|||
слагаемого другое будет уменьшаться, т. е. если x возрастает, то y уменьшается, и наоборот.
Следовательно, эллипс имеет форму овальной замкнутой кривой.
54
Аналогичные рассуждения справедливы для эллипса с фокусами, расположенными симметрично относительно начала координат на оси
Оу.
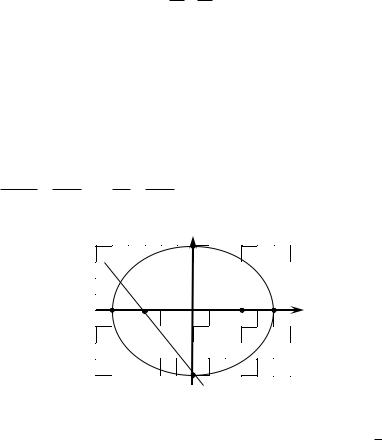
Пример 1. Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением
x2 y2 1. 25 16
Сделать построение.
Р еше н ие . Данное уравнение определяет эллипс с фокусами, расположенными симметрично относительно начала координат на оси
Ох.
Большая его полуось а = 5, а меньшая b = 4. Найдем полуфокусное расстояние: c2 = a2 – b2 = 25 – 16 = 9, т. е. c = 3, а фокусы эллипса находятся в точках F1(–3; 0), F2(3; 0). Нижняя вершина эллипса будет находиться в точке В1(0; –4).
Тогда уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, будет иметь вид
x 0 |
|
y |
4 |
; |
x |
|
y 4 |
; 4x 3y 12; |
4x 3y 12 0 . |
|
3 0 |
|
0 |
4 |
|
3 |
|
4 |
|
|
|
Сделаем построения (рис. 28). |
|
|
|
|||||||
|
|
|
|
|
|
|
|
y B2 |
|
|
|
|
|
|
А1 |
|
F1 |
|
O 1 |
F2 |
A2 x |
B1 |
Рис. 28
Пример 2. Построить эллипс с вершиной в начале координат, если
известно, что один из его фокусов находится в точке М(0; – 
 2 ), а большая ось равна 4.
2 ), а большая ось равна 4.
Р еше н ие . Так как фокус расположен на оси ординат, а его вершина совпадает с началом координат, то каноническое уравнение
55
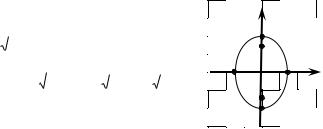
эллипса будет иметь вид |
|
x2 |
|
|
y2 |
1 , |
причем |
||||||||||||
|
b2 |
|
a2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
большая |
полуось |
а = 2, |
а |
|
полуфокусное |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
расстояние с = |
2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Известно, |
|
|
|
что |
|
|
меньшая |
|
|
полуось |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
определяется как b |
|
a2 c2 |
|
|
|
4 2 2. |
|||||||||||||
Тогда |
каноническое |
уравнение |
эллипса |
||||||||||||||||
примет вид |
x2 |
|
|
y2 |
1 . |
Сделаем |
построения |
||||||||||||
|
|
|
|||||||||||||||||
|
|
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(рис. 29).
y |
|
|
2 |
А1 |
|
F2 |
|
|
B1 |
|
B2 |
O |
1 |
x |
F1 |
|
|
|
A2 |
|
Рис. 29 |
|
|
4.14. Окружность, ее канонические уравнения
Окружность – это линия, состоящая из множества точек плоскости, равноудаленных от заданной точки, называемой центром окружности.
Уравнение окружности с центром в начале координат радиусом R имеет вид x2 y2 R2 .
Очевидно, что данное уравнение является частным случаем канонического уравнения эллипса, когда его большая и меньшая полуоси равны. Действительно, пусть a = b = R, тогда каноническое уравнение эллипса можно записать в виде
x2 |
|
y2 |
1. |
|
R2 |
R2 |
|||
|
|
Умножим левую и правую части этого уравнения на R2, в результате получим x2 y2 R2 – уравнение окружности. В данном
случае говорят, что фокусы эллипса совпадают с вершиной, а сам эллипс вырождается в окружность.
4.15. Гипербола, ее канонические уравнения
Гиперболой называется линия, состоящая из всех точек плоскости, для каждой из которых модуль разности расстояний до двух данных точек F1 и F2, называемых фокусами гиперболы, есть величина постоянная, равная 2а, меньшая, чем расстояние 2с между фокусами.
56

Величину а для гиперболы называют действительной полуосью, а
с – полуфокусным расстоянием (а <c).
Уравнения гиперболы, фокусы которой располагаются симметрично относительно начала координат и лежат на одной из осей называются каноническими уравнениями.
Каноническое уравнение гиперболы с фокусами, расположенными на оси Ох симметрично относительно начала координат (рис. 30) имеет вид
x2 |
|
y 2 |
1 |
|
a2 |
b2 |
|||
|
|
где b2 = c2 a2 0 (b – мнимая полуось эллипса).
|
y |
|
2a |
|
|
|
|
|
|
|
|
|
M(x; y) |
|
|
2b |
|
|
|
F1 |
|
O |
F2 |
x |
|
|
|
|
|
2c
Рис. 30
Прямоугольник со сторонами 2а и 2b по оси Ох и Оу соответственно, диагонали которого пересекаются в точке начала координат называют основным прямоугольником гиперболы.
Каноническое уравнение гиперболы с фокусами и действительной осью 2b, расположенными на оси Оу симметрично относительно начала координат, и мнимой осью 2а на оси Ох (рис. 31) имеет вид
|
y2 |
|
|
x2 |
|
1. |
|
|
|
|
|
||
|
b2 |
a2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
Нетрудно заметить, что |
|
гипербола |
|
y 2 |
|
x2 |
1 имеет общий |
||||||
|
b2 |
a2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
прямоугольник с гиперболой |
|
x2 |
|
y2 |
1 |
. Такие гиперболы называют |
|||||||
|
a2 |
b2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||
сопряженными.
Исследуем форму гиперболы (рис. 30).
57

y
F2
2b
O |
2c |
x |
|
|
2a
F1
Рис. 31
1.Канонические уравнения гиперболы содержат переменные х и у в четных степенях, поэтому любая точка гиперболы будет иметь на ней симметричные точки относительно осей координат и начала координат. При этом начало координат называют центром гиперболы.
2.Найдем точки пересечения гиперболы с осями координат. Точками пересечения гиперболы с осью Ох являются точки
A1(–a; 0) и A2(a; 0). Их называют вершинами гиперболы, а отрезок
A1A2 = 2а – действительной осью.
Гипербола не имеет точек пересечения с осью Оу. |
|
||||
Отрезок В1В2 = 2b, соединяющий точки В1(0; –b) и В2(0; |
b), |
||||
называется мнимой осью гиперболы. |
|
||||
3. Разрешим уравнение |
x2 |
|
y 2 |
1 относительно переменной у. |
В |
a2 |
|
||||
|
|
b2 |
|
||
результате получим
y ba 
 x2 a2 .
x2 a2 .
Знаки правой части данных равенств характеризуют фрагменты графика гиперболы, на которые она разбивается осью Ох. Знак «+» соответствует фрагменту графика, лежащему над осью Ох, а «–» – под этой осью. Равенства определены для значений переменной х, изменяющихся в пределах x (– ; –a] [a; ).
Рассмотрим данные уравнения при неограниченном удалении переменной х влево и вправо от начала координат. В этом случае
58

постоянной величиной, стоящей под знаком корня можно пренебречь и уравнения примут вид
|
|
|
y |
b |
|
|
|
|
b |
x. |
|
|
|
|
|
|
x2 |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
a |
|
|
a |
||||
Уравнения y |
b |
x и |
y |
b |
x |
определяют прямые, пересека- |
|||||
|
a |
|
|
a |
|
|
|
|
|||
ющиеся в начале координат и являющиеся продолжением диагоналей основного прямоугольника гиперболы. Можно показать, что при неограниченном удалении переменной х от начала координат расстояние от точки гиперболы до одной из этих прямых стремится к
нулю. Поэтому прямые y ba x и y ba x называются асимптотами
гиперболы.
Разрешим уравнение относительно переменной х, получим x ba 
 b2 y2 .
b2 y2 .
Знак «+» будет соответствовать фрагменту графика гиперболы, лежащему правее оси Оу, а «–» – левее этой оси. Равенство определено для любого значения переменной y.
4. В рассматриваемом уравнении разность неотрицательных
|
x2 |
|
y 2 |
|
слагаемых |
|
и |
|
равна единице. Следовательно, при увеличении |
a 2 |
b2 |
|||
одного слагаемого другое будет тоже возрастать, т. е. при возрастанииx увеличивается и y , и наоборот.
Из приведенных исследований следует, что гипербола – это кривая, состоящая из двух неограниченных ветвей, имеющая форму, изображенную на рис. 30.
Аналогичные рассуждения справедливы для гиперболы с фокусами, расположенными симметрично относительно начала координат на оси Оу.
При построении гиперболы целесообразно сначала построить основной прямоугольник гиперболы и отметить ее вершины. Затем продлить диагонали основного прямоугольника гиперболы на бесконечность, получив при этом ее асимптоты. Расставить точки относительно асимптот, характеризующие неограниченное приближение к ним ветвей гиперболы вдоль действительной оси. Соединить плавной линией эти точки с вершинами гиперболы.
59

Пример. Составить каноническое уравнение гиперболы с фокусами расположенными симметрично относительно начала координат на оси Оу, проходящей через точки А (–5; 4) и В (1; –1). Найти полуоси, фокусы, уравнения асимптот гиперболы. Сделать построения.
Р еше н ие . Каноническое уравнение гиперболы с фокусами, расположенными симметрично относительно начала координат на оси
Оу, имеет вид |
y 2 |
|
x2 |
1. |
|
b2 |
a2 |
||||
|
|
|
Так как точки А и В лежат на гиперболе, то их координаты удовлетворяют ее уравнению. В результате подстановки координат точек получаем систему уравнений двух неизвестных а и b:
16 |
|
25 |
1 |
|||
|
|
|
||||
b2 |
a2 |
|||||
|
1 |
|
1 |
. |
||
|
|
1 |
||||
|
|
2 |
a |
2 |
||
b |
|
|
|
|
||
Исключим из системы, например, переменную b. Для этого второе уравнение системы умножим на 16 и вычтем из первого уравнения
второе. В результате уравнение примет вид a92 15 , откуда a2 = 53 .
Подставив a2 во второе уравнение системы, получим b2 = 83 .
Таким образом, каноническое уравнение гиперболы с фокусами, расположенными симметрично относительно начала координат на оси Оу, проходящей через точки А(–5; 4) и В(1; –1), будет иметь вид
y 2 x2 1. 38 35
3
При этом действительная полуось гиперболы b= 
 0,612, а
0,612, а
8
мнимая a= 
 53 0,775.
53 0,775.
Найдем полуфокусное расстояние
с = 
 b2 a2
b2 a2 
 83 53
83 53 
 3940 0,987.
3940 0,987.
60
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
||
Тогда фокусы гиперболы будут находиться в точках |
F |
|
0; |
|
|
|
и |
|
|
||||||||
|
1 |
|
|
|
40 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
5 |
|
|
||||
F |
|
0; |
|
|
|
|
.Уравнения асимптот гиперболы примут вид: |
y |
|
x и |
|||||
2 |
|
|
|
|
40 |
|
|
|
|
|
8 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
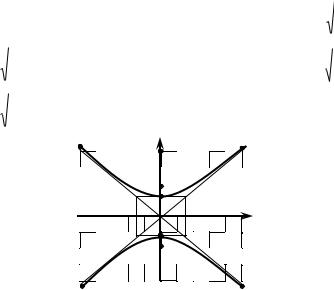
y |
|
5 |
|
x. Сделаем построения (рис.32). |
|
|
|
|
|
||||||
|
8 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
F2 |
|
|
A2 |
|
|
|
|
B2 |
|
B1 |
O |
1 |
x |
|
|
А1 |
|
F1 |
Рис. 32 |
4.16. Парабола, ее канонические уравнения
Параболой называется множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и данной прямой, называемой директрисой, лежащих в той же плоскости.
Ось симметрии параболы, вдоль которой располагаются ее ветви, называется осью параболы, а точка пересечения параболы с осью – вершиной параболы. Отрезок прямой, соединяющий любую точку параболы с фокусом, называется фокальным радиусом.
Параболу с вершиной в начале координат на плоскости можно
определить следующими каноническими уравнениями: y2 = 2px, y2 = –2px, x2 = 2py, x2 = –2py.
Первые два из них задают параболы с ветвями, направленными вправо и влево вдоль оси Ох, а два последующих уравнения – параболы вдоль оси Оy с ветвями направленными вверх и вниз.
Величину р (расстояние от фокуса до директрисы) называют
параметром параболы.
61
Построим параболу с вершиной в начале координат и ветвями, направленными вправо вдоль оси Ох. Для этого фокус параболы расположим на оси Ох, а директрису – параллельно оси Оу так, чтобы
фокус и директриса отстояли от оси Оу на равных расстояниях |
p |
||||||
|
|||||||
2 |
|||||||
|
|
|
|
|
|
||
(рис. 33). |
|
|
|
|
|||
|
|
y |
|
|
|
|
|
А |
M(x; y) |
|
|
||||
|
|
|
|
|
|||
|
p |
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
O |
p |
F |
x |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
x 2p
Рис. 33
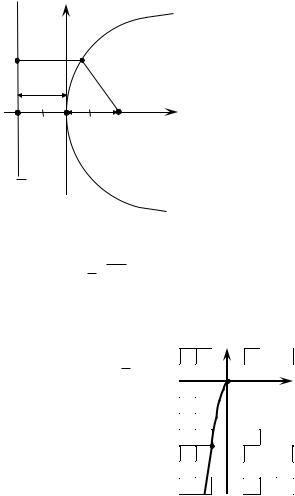
Пример. Построить линию, определяемую уравнением x 12 
 y .
y .
Реше н ие . Из уравнения видно, что оно определено только при x≤0
иy≤0, т. е. это уравнение задает лишь фрагмент некоторой кривой, лежащей в третьей четверти координатной плоскости.
Возведем в квадрат левую и правую часть
|
|
|
|
x2 |
1 ( y) |
|
y |
|
|
|
уравнения, в результате получим |
|
|
|
|
||||||
|
|
|
|
|
4 |
|
|
|
1 |
|
или |
y 4x2 . |
Это |
уравнение |
параболы |
с |
– 1 |
O |
x |
||
|
|
|||||||||
вершиной в начале координат и ветвями, |
|
|
|
|
||||||
направленными вниз, вдоль оси Оy. |
|
|
|
|
|
|
||||
Проанализировав |
результаты, |
делаем |
|
–4 |
|
|
||||
вывод, что данное |
уравнение определяет |
на |
|
|
|
|||||
|
|
|
|
|||||||
62 |
Рис. 34 |
|
