диплом / Задачі_фізичного_змісту_при_вивченні_математики_в_загальноосвітній_школі

11х + 7х £ 3;

154

18х £ 462;

х£ 462 ; 18

х£ 25 2 . 3

Відповідь: туристи можуть відплисти на відстань ≈25 км.

Задача 29.

При вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше. Знайдіть глибину шахти, якщо камінець досяг її дна через 8 с після початку падіння.

Розв’язання:

За першу секунду тіло проходить 4,9 м, а за кожну наступну на 9,8 м більше. Час падіння дорівнює 8 с. Отримаємо арифметичну прогресію, в якій: a1 = 4,9м, d = 9,8м, n = 8. Знайдемо, скільки метрів

тіло пролетить за останню секунду: a8 = 4,9 + 7 × 9,8 = 73,5. Глибина

шахти дорівнюватиме сумі всіх відстаней, які тіло пролетіло за кожну секунду, а це чисельно дорівнює сумі 8 перших членів арифметичної прогресії:

Відповідь: глибина шахти дорівнює ≈ 314 м.

41

Задача 30.

Скільки секунд падала б гайка з висоти 490 м? Розв’язання:

Із фізики відомо, що при вільному падінні тіло проходить за першу секунду 4,9 м, а за кожну наступну на 9,8 м більше (при умові, що початкова швидкість дорівнює нулю). Отримаємо арифметичну прогресію, в якій a1 = 4,9м; d = 9,8м і Sn = 490м (оскільки всього

гайка пролетіла 490 м). Нам необхідно знайти, скільки секунд падала гайка, що відповідає числу членів даної арифметичної прогресії n . Нам невідомо, скільки метрів пролетіла б гайка за останню секунду, тобто, нам невідомо, чому дорівнює an . Тому складаємо систему

рівнянь:

490 = 4,9 + 4,9 + (n − 1)9,8 × n; 2

9,8n2 = 980; n2 = 100;

n1, 2 = ±10.

Від’ємне значення кореня не задовольняє умову задачі, таким чином, n = 10.

Відповідь: з висоти 490 м гайка падала б 10 с.

Задача 31.

Катер за 4 год пройшов 24 км за течією річки і 20 км проти течії. Знайдіть швидкість течії, якщо власна швидкість катера

дорівнює 12 км .

год

Розв’язання:

Позначимо швидкість течії через х. Швидкість катера за течією

дорівнює (12 + х) км , швидкість катера проти течії дорівнює

год

42

Від’ємне значення кореня не задовольняє умову задачі. Таким

чином, x = 1 + 7 = 4. 2

Відповідь: швидкість течії річки дорівнює 4 км .

год

Задача 32.

З порту одночасно вийшли два теплоходи: один на південь, другий на захід. Через дві години відстань між ними становила 60 км.

Знайдіть швидкості теплоходів, якщо різниця цих швидкостей 6 км .

год

Розв’язання:

Нехай x км — швидкість

год

першого теплохода, тоді швидкість

перпендикулярні між собою. За 2

2(х + 6)км. За теоремою Піфагора запишемо:

43

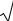
4x2 + 4(x + 6)2 = 602 ;

4x2 + 4(x2 + 12x + 36) = 3600; x2 + x2 + 12x + 36 = 900;

2x2 + 12x − 864 = 0;

годину з А виїхав автомобіль, який наздогнав спочатку другого велосипедиста, а через 10 хв і першого. Знайдіть швидкість автомобіля.

44

1 x = 18 + 6;

3

1 x = 24;

3

x = 72.

Відповідь: швидкість автомобіля дорівнює 72 км .

год

45

Задача 34.

Виміряти питому теплоту плавлення льоду, використовуючи той факт, що швидкість теплообміну води, взятої при 0 ° С, і льоду, взятого при 0° С, з повітрям однакова.

Розв’язання:

де τ1 – час нагрівання, τ 2 - час плавлення льоду, взятого при

0° С.

θ1 = cm1 (t2 − t1 ),θ 2 = λm2 ,

звідси маємо:

λ= c(t2 − t1 )τ 2 .

τ1

Відповідь: питома теплота плавлення льоду: λ = c(t2 − t1 )τ 2 .

τ 1

Задача 35.

Виміряти питому теплоту плавлення льоду, використовуючи рівняння теплового балансу для випадку змішування води і льоду, температура яких різна в різних агрегатних станах.

Розв’язання:

θ1 = θ 2 +θ 3 ,

θ1 = cm1 t1 – кількість теплоти, необхідна для плавлення льоду;

θ2 = λm2 – кількість теплоти, необхідна для плавлення льоду;

θ3 = cm2 t2 – кількість теплоти, необхідна для нагрівання води,

отриманої із льоду;

cm1 t1 = λm2 + cm2 t2 ,

λ = c(m1 t1 − m2 t2 ). m2

.

Відповідь: питома теплота плавлення льоду рівна:

λ = c(m1 t1 − m2 t2 ). m2

46

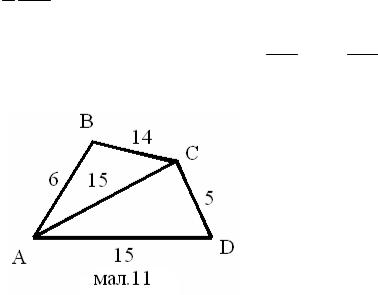
Задача 36.

Міста A,B,C,D, розміщені так, що чотирикутник ABCD – опуклий, з’єднані прямолінійними доріжками AB, BC, CD, AD і AC. Їх довжини відповідно рівні 6, 14, 5, 15 і 15 км. Із одного із цих міст одночасно вийшли три туристи, які йшли без зупинок з постійною швидкістю. Маршрути всіх туристів різні, причому кожен з них складається з трьох доріг і проходить через всі міста. Перший і другий туристи перед проходженням третіх доріг своїх маршрутів зустрілися в одному місті, а третій закінчив маршрут на годину раніше туриста, який закінчив маршрут останнім. Знайдіть швидкості туристів, якщо швидкість третього більша швидкості другого і на

1 км менша швидкості першого, причому швидкості всіх туристів

2 год

знаходяться в інтервалі від 5 км до 8 км .

год год

Розв’язання:

Позначимо швидкості туристів

1)Зауважимо спочатку, що якщо у якихось туристів співпадають перші два відрізки шляху, то повинні повністю співпадати їх маршрути. За умовою кожен маршрут складається із трьох відрізків і проходить через всі чотири міста. За умовою всі маршрути різні. Значить, можна зробити висновок, що у двох будь-яких туристів шляхи відрізняються уже після проходження перших двох доріг.

2)Якщо туристи вийшли із міста А, то хто-небудь з них повинен йти по діагоналі АС, але тоді він не зможе пройти через всі чотири міста (його маршрут складається тільки з трьох відрізків). Тобто, туристи не могли вийти з міста А. З аналогічних причин не могли вони вийти із міста С. Тобто, туристи вийшли з міста В чи з міста D.

3)За умовою перший і другий туристи зустрілись перед

47

проходженням третіх доріг, тому перший і другий туристи вийшли по різних дорогах і зустрілись в протилежній вершині чотирикутника. Оскільки υ1 > υ2 , то довжина шляху першого

туриста до зустрічі з другим рівна AB + AD = 21, а довжина шляху другого до тієї ж зустрічі рівна BC + CD =19.

υ= 19υ .

12

4)Другий відрізок шляху третього туриста співпадає зОтримаємо

АС, а довжина всього шляху рівна або

BC + CA + AD = 44,

чи

AB + AC + CD = 26.

В першому випадку шлях третього туриста найдовший. Оскільки υ1 > υ3 , то перший турист прийшов раніше третього.

В першому випадку третій турист повинен прийти в кінцевий пункт останнім, але це суперечить умові задачі. Тобто, довжина шляху третього туриста рівна не 44 км, а 26 км.

5) Нехай туристи вийшли із міста В. Тоді шлях першого – BADC, шлях другого – BCDA, шлях третього – BACD. Довжини шляхів рівні відповідно 26 км, 34 км, 26 км, а час, затрачений на всю дорогу,

υ3 ≤ υ2 , що суперечить умові.

48

Отже, туристи вийшли з міста D, шлях першого – DABC, другого – DCBA, третього – DCAB. Довжини шляхів рівні відповідно 35 км, 25 км, 26 км, а час на всю дорогу рівний

рівняння рівні 7 і 5 . За умовою, швидкості розміщені в проміжку від

2 5 до 8 кілометрів, значить, другий корінь не підходить. Тобто,

туриста становить 6 1 км . 2 год

Задача 37.

Із пункту А в пункт В доставлена пошта. Спочатку її віз

мотоцикліст; проїхавши 2 відстані від пункту А до пункту В, передав

3

49

пошту велосипедисту, який на нього чекав і який доставив її в пункт В (час, який потрібний був на передачу пошти, вважається рівним нулю). При цьому пошта була доставлена із пункту А в пункт В за проміжок часу, необхідний, щоб проїхати від пункту А до пункту В з

швидкістю 40 км . Відомо, що якби мотоцикліст і велосипедист

год

виїхали із пунктів А і В одночасно назустріч один одному, то вони зустрілися б через проміжок часу, який необхідний для проїзду від

пункту А до пункту В з швидкістю 100 км . Знайдіть швидкість

год

мотоцикліста, враховуючи, що вона більша швидкості велосипедиста. Розв’язання:

Позначимо через S км відстань між пунктами А і В; нехай x км

дорівнювати S годин. Тому маємо перше рівняння

40

2× S + 1 × S = S .

3x 3 y 40

Якби мотоцикліст і велосипедист виїхали назустріч один

задачі повинен дорівнювати S годин. Тому маємо друге рівняння

100

S = S .

x+ y 100

Для знаходження х і у отримали після ділення правої і лівої частини кожного рівняння на S (S ¹ 0) систему

50