
диплом / Задачі_фізичного_змісту_при_вивченні_математики_в_загальноосвітній_школі
.pdf
Відповідь: маса всього стержня становить 360 г, а лінійна
густина в точках А становить 0 |
г |
, а в точці В становить 60 |
г |
. |
см3 |
|
|||
|
|
см3 . |
||
2.ЗАДАЧІ НА НАЙБІЛЬШЕ І НАЙМЕНШЕ ЗНАЧЕННЯ
Проблема знаходження найменших та найбільших значень відіграє важливу роль в фізиці, техніці та економіці. Мова йде про визначення оптимально можливих значень фізичних і інших величин, економії часу, енергії, матеріалів, про попередження аварійних ситуацій і ін.
Запропоновані задачі носять вибірковий характер, вони лише в невеликій мірі відображають масштабність цієї проблеми.
Задача 1.
Електричні заряди q1 = 5нКл і q2 = 11нКл розміщені на відстані r
один від одного. Яким чином слід перерозподілити заряди, щоб сила взаємодії між ними була найбільшою?
Розв’язання:
За законом Кулона сила взаємодії між зарядами
F = k × q1 × q2 . r 2
Відповідь: оскільки k і r є сталими, то щоб отримати максимальну силу, треба лише перерозподілити заряди. Для отримання найбільшої сили потрібно від q2 відняти 3нКл і
передати q1 .
Задача 2.
Електричне коло складається з двох паралельно з’єднаних провідників. При якому співвідношенні між опорами цих провідників опір найбільший, якщо при послідовному з’єднанні опір кола дорівнює 6 Ом?
Розв’язання: При послідовному з’єднанні: R = R1 + R2 ,
при паралельному— |
1 |
= |
1 |
+ |
1 |
, R = |
R1 R2 |
. |
||
|
|
|
|
|||||||
|
|
R R1 |
|
R2 |
|
R1 + R2 |
||||
Оскільки |
R1 + R2 = 6 = const , то |
R1R2 досягає найбільшого |
||||||||
значення при R1 |
= R2 = 3(Ом) і, відповідно, |
|||||||||
11

R = |
R1 R2 |
= |
9 |
= 1,5. |
||
R1 |
+ R2 |
6 |
||||
|
|
|
||||
Зауваження: при розв’язуванні двох останніх задач була використана теорема:
Добуток двох додатних множників, сума яких є сталою, має найбільше значення при рівності множників.
Покажемо ще один спосіб розв’язування останньої задачі.
R = |
R1 R2 |
= |
R1 (6 − R1 ) |
, |
||
R1 + R2 |
|
|||||
|
6 |
|
||||
′ |
|
1 |
(6 − 2R1 ), 6 − 2R1 = 0, R1 = 3, R2 = 3, |
|||
|
|
|||||
R (R1 ) = |
6 |
|||||
|
|
|
|
|
|
|
R′′(R1 ) < 0
і ми маємо максимум.
Відповідь: при співвідношенні R′′(R1 ) < 0 між опорами цих провідників опір найбільший.
Задача 3.
Річка шириною 120м тече зі швидкістю 1,5 м . Човняр, який
с
може гребти зі швидкістю 2,5 м, хоче досягти протилежного берега в
с
найкоротший час. Знайдіть цей час і напрям руху човняра відносно берега.
12

Розв’язання:
Для досягнення поставленої цілі необхідно, щоб результуюча швидкість була направлена перпендикулярно до берегів річки (найменшій відстані відповідає найменша затрата часу) (мал.1)
υ = |
|
υ 2 |
−υ 2 |
= |
|
|
|
|
|
||||||
|
|
|
|
ч |
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
м 2 |
|
м 2 |
|
м |
|||||||||
= |
2,5 |
|
|
|
|
|
− 1,5 |
|
|
= 2 |
|
, |
|||
|
|
|
|
|
|
||||||||||
|
|
с |
|
с |
|
с |
|||||||||
tmin |
= |
120 |
= 60(c), |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
tgα = |
2 |
|
|
≈ 1,33, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
1,5 |
|
|
|
|
|
|
|
|
||||||
α ≈ 53°.
Відповідь: час, за який човняр досягне протилежного берега, становить 60 с, напрям руху човняра відносно берега становить ≈ 53°.
Задача 4.
Між точками А і В рухається по прямій тіло так, що виходячи з точки А з початковою швидкістю υ0 = 0 , воно повинно мати
в точці В швидкість υ = 0 . При цьому тіло може рухатися з сталим за модулем прискоренням і рівномірно. Яким має бути характер руху, щоб час руху був мінімальним?
Розв’язання:
Пройдений шлях може бути зображений у вигляді площі трапеції чи трикутника (мал.2).
13
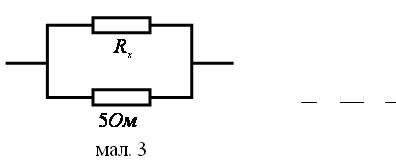
SA B C |
= SA AB |
C |
2 |
= SA A B C |
, |
|||||
1 |
1 |
1 |
1 |
2 |
|
1 |
3 |
3 |
3 |
|
A1C1 |
< A1C2 < A1C3 |
|
|
|
||||||
або
t1 < t2 < t3 .
Відповідь: першу половину часу тіло повинно рухатись рівноприскорено, а другу половину рівносповільнено.
В задачі ми використали деяке твердження, яке доцільно було б довести.
Твердження. Якщо рівність: |
|
||||||||||||||
|
|
|
1 |
= |
1 |
+ |
1 |
+ ... + |
1 |
, |
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
а |
|
|
|
а1 |
а2 |
|
|
ап |
|
|||
|
|
де а > 0, a1 |
> 0, a2 > 0, ..., an |
> 0, то |
|||||||||||
|
|
а < a1 , a < a2 , ..., a < an . |
|
||||||||||||
Доведення: |
|
|
|
|
|
|
a1 − a |
|
|
|
|
||||
|
1 |
− |
1 |
> 0, |
|
> 0, a > a, a < a і т.д. |
|||||||||
|
|
|
|
||||||||||||
|
a |
|
a1 |
|
|
1 |
1 |
||||||||
|
|
|
aa1 |
|
|||||||||||
Дане твердження має велике практичне значення в фізиці, електротехніці і ін.
Задача 5.
Електричне коло має деякий опір (значення цього опору може бути відомим або невідомим). Потрібно змінити опір кола так, щоб
він став меншим 5 Ом.
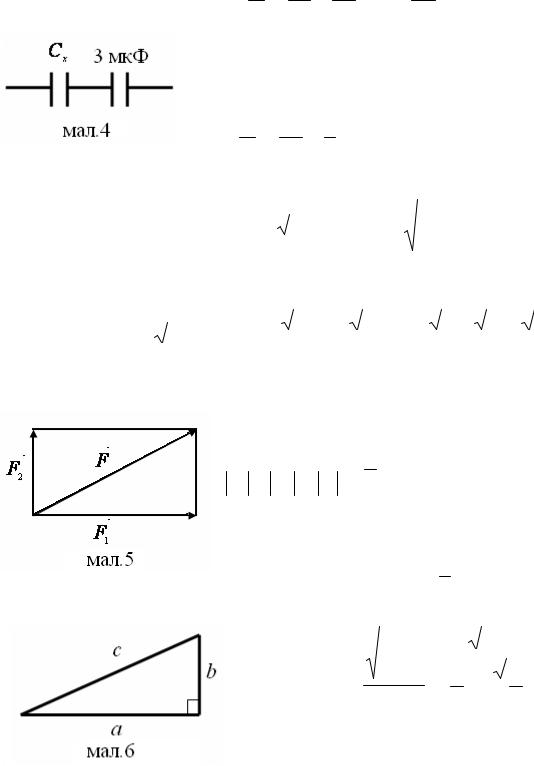
Для розв’язання цієї задачі достатньо паралельно підключити провідник з опором R ≤ 5Ом (мал.3).
1 = 1 + 1 , R < 5.
R Rx 5
Задача 6.
До конденсатора ємності Сх треба приєднати інший так, щоб в
результаті отримали ємність, меншу 3мкФ. Розв’язання:
При послідовному з’єднанні конденсаторів:
14
1 = 1 + 1 + ... + 1 .
С С1 С2 Сп
До конденсатора ємності Сх треба
послідовно підключити інший конденсатор ємністю С ≤ 3мкФ.(мал.4).
1 = 1 + 1 , С < 3 .
ССх 3
Теорема: якщо a > 0 i b > 0 , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a + b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
£ |
|
|
£ |
£ |
|
a2 + b2 |
. |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
ab |
|
||||||||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||||||
+ |
2 |
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
a |
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доведення. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
2ab |
|
|
= |
2ab - a |
|
- b |
|
|
= - |
|
( |
|
- |
|
)2 |
|
||||||||||||||
|
- |
|
ab |
ab |
ab |
a |
b |
£ 0. |
|||||||||||||||||||||||
|
ab |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
a + b |
|
|
|
a + b |
|
|
|
|
|
|
a + b |
|
||||||||||||||||||
(Інші нерівності доводяться аналогічно).
Задача 7.
Доведіть, що коли дві сили F1 і F2 прикладені до однієї точки під кутом 90° , то F1 + F2 £ F × 
 2 , де F - рівнодійна F1 i F2 .
2 , де F - рівнодійна F1 i F2 .
Сформулюємо задачу по-іншому. Доведіть, що в прямокутному трикутнику найбільше значення суми довжин катетів
дорівнює довжині гіпотенузи, помноженої на 
 2 (мал.5, 6). Доведення.
2 (мал.5, 6). Доведення.
a + b |
£ |
|
a2 + b2 |
|
= |
|
a2 + b2 |
, |
||
2 |
|
|
|
|
|
|||||
2 |
2 |
|
|
|||||||
a + b £ 
 a2 + b2 ×
a2 + b2 × 
 2 = c
2 = c
 2.
2.
Задача 8.
Визначте мінімальну відстань між предметом і його дійсним зображенням в збиральній лінзі з фокусною відстанню F .
Розв’язання. Перший спосіб розв’язування:
15

1 |
+ |
1 |
= |
1 |
— формула |
тонкої |
|
|
|
d f F
лінзи, де d - відстань від предмета до лінзи, f - відстань від лінзи до зображення предмета, F – фокусна відстань.
|
|
|
|
|
|
|
d + f |
|
³ |
|
|
|
|
|
2 |
|
|
|
= |
|
2df |
, |
|||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
+ |
|
1 |
|
|
|
|
|
d + f |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
f |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
(d - f )2 |
|
³ 0. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
2(d + f ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
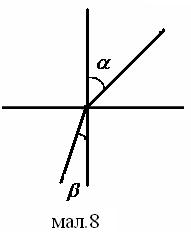
Найменшій відстані d + f |
відповідає |
d = f (мал.7). |
|||||||||||||||||||||||||||||||
З |
1 |
+ |
1 |
= |
1 |
знаходимо |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
d f |
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 |
= |
2 |
, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
d = 2F , |
|
|
|
|
|
|
|
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d 2 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
a = |
|
|
|
, |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d - F |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
d + f = 4F. |
|
|
|||||||||||||||||||||
Другий спосіб: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Нехай d + f |
= a, f = a − d , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 |
+ |
|
|
|
1 |
|
|
|
|
|
= |
|
1 |
, |
|
|||||||||||
|
|
|
|
|
|
|
a |
|
- d |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
F |
|
|
||||||||||||
|
|
|
|
|
|
|
|
a = |
d 2 |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
d - F |
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
d 2 |
|
- ad + aF = 0, |
|
||||||||||||||||||||||
|
|
|
|
|
|
d = |
a ± |
|
|
|
, |
|
|
||||||||||||||||||||
|
|
|
|
|
|
a 2 |
|
- 4aF |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a 2 - 4aF ³ 0,
amin = 4F або (d + f )min = 4F.
16
Третій спосіб: |
|
|
|
|
|
(d − 2F )2 |
|
||
f = |
dF |
, d + f = |
dF |
+ d = |
d 2 |
= |
+ 4F. |
||
d − F |
d − F |
d − F |
d − F |
||||||
|
|
|
|
|
|||||
При d = 2F маємо найменшу відстань, що дорівнює 4F . Четвертий спосіб:
d + f = |
|
d |
2 |
; |
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
d − F |
|
|
|
||||
(d + f ) |
′ |
= |
|
2d (d − F ) − d 2 |
= |
d 2 − 2dF |
|||
|
|
|
|
|
|||||
|
|
(d − F )2 |
; |
||||||
( d ) |
|
|
|||||||
|
|
|
|
|
|
|
(d − F )2 |
||
d 2 − 2dF = 0, d = 2F. При d = 2F f = 2F, a d + f = 4F.
Принцип Ферма
П’єр Ферма (1601-1665 рр.) в результаті розв’язування багатьох задач проголосив так званий принцип найменшої дії. Згідно цього принципу природа змушує всі явища відбуватися з найменшою затратою енергії, часу і ін. (Принцип Ферма не є універсальним). Наприклад, світло вибирає із всіх можливих траєкторій, що з’єднують
дві точки, ту, яка вимагає найменшого часу. Якщо застосовувати принцип Ферма до
закону заломлення світла— час проходження границі двох середовищ мінімальний при
υ1 |
= |
sin α |
, де υ |
|
i υ |
— швидкості поширення |
|
|
1 |
||||
υ2 |
|
sin β |
2 |
|
||
|
|
|
|
|||
світла в різних середовищах, наприклад в повітрі і воді, α— кут падіння, β— кут заломлення. (мал.8)
Задача 9.
Пішохід повинен пройти з пункту А, що знаходиться на одному тротуарі, в пункт В, що знаходиться на другому тротуарі. Знаючи, що швидкість руху по тротуару в µ раз (µ>1) більша, ніж по бруківці, визначте, під яким кутом φ пішохід повинен перейти вулицю для того, щоб подолати шлях в найкоротший час.
17
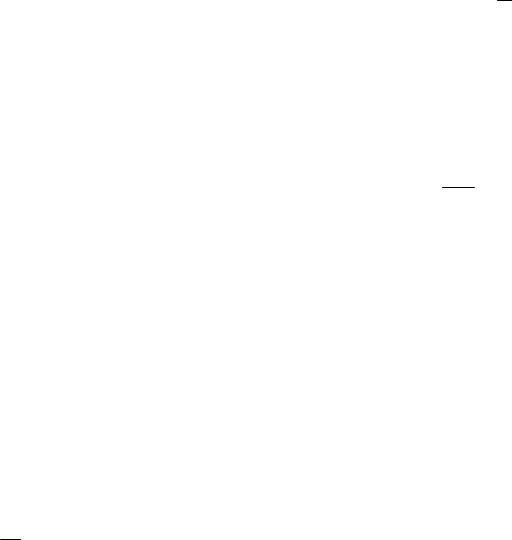
|
|
Розв’язання: |
|
|
|||
υ |
= |
sin(90° − α ) |
, |
1 |
= cosϕ , ϕ = arccos |
1 |
. |
μυ |
sin 90° |
μ |
|
||||
|
|
|
μ |
||||
Якщо допустити, наприклад, що µ=2,то ϕ = 60° .
Відповідь: для того, щоб подолати шлях в найкоротший час,
пішохід повинен перейти вулицю під кутом ϕ = arccos μ1 .
3.РОЗВ’ЯЗУВАННЯ СЮЖЕТНИХ ЗАДАЧ МЕТОДОМ РІВНЯНЬ
Задача 1.
Катер у стоячій воді йде зі швидкістю 20 км . Швидкість течії
|
|
|
|
|
год |
|
|
|
||
річки 2 |
км |
. Знайдіть відстань між двома пристанями, |
якщо рейс |
|||||||
|
||||||||||
|
год |
|
|
|
|
|
|
|
|
|
туди й назад катер здійснює за 5 год. |
|
|
|
|||||||
|
|
|
|
|
Розв’язання: |
|
|
|
||
Швидкість |
катера |
за течією дорівнює 20 + 2 = 22( |
км |
) ; |
||||||
|
||||||||||
|
|
|
|
|
|
|
|
|
год |
|
швидкість катера проти течії дорівнює 20 − 2 = 18( |
км |
) . |
|
|
|
|||||
|
|
|
|
|||||||
|
|
|
|
|
|
год |
|
|
|
|
Нехай x — |
відстань між двома пристанями. Тоді, |
пливучи за |
||||||||
течією, катер витрачає |
x |
годин; а, пливучи проти течії, витрачає |
||||||||
|
||||||||||
|
|
|
22 |
|
|
|
|
|
|
|
x годин. 18
Отримаємо:
x |
+ |
x |
= 5, звідси |
9x + 11x |
= 5, 20x = 990, x = 49,5. |
22 |
|
|
|||
18 |
198 |
|
|||
Відповідь: відстань між пристанями 49,5 км.
18

Задача 2.
Катер у стоячій воді проходить 15 км , швидкість течії річки
год
2 км . Знайдіть відстань між двома пристанями, якщо в один бік
год
катер проходить її на півгодини швидше, ніж у другий. Розв’язання:
Нехай відстань між двома пристанями х км. Швидкість катера за течією дорівнює: 15 км + 2 км = 17 км , швидкість катера проти
|
|
|
|
|
|
год |
год |
год |
|
|
|
||
течії — 15 |
км |
− 2 |
км |
= 13 |
км |
. Пливучи за течією, |
катер витрачає |
||||||
год |
год |
год |
|||||||||||
|
x |
|
|
|
|
|
|
x |
|
||||
|
годин. Пливучи проти течії, |
катер витрачає |
|
годин. Тоді |
|||||||||
17 |
|
||||||||||||
|
|
|
|
|
|
|
|
13 |
|||||
отримаємо: x = x − 1 , звідси
17 13 2
x − x = − 1 , 17 13 2
13x − 17x = − 1 ,
|
|
221 |
2 |
|
|
|
|
|
− 4x = − |
221 |
, x ≈ 27,6. |
||
|
|
2 |
||||
|
|
|
|
|
|
|
|
Відповідь: відстань між пристанями дорівнює 27,6км. |
|||||
|
|
Задача 3. |
||||
|
Відстань ніж двома станціями потяг може проїхати зі швидкістю |
|||||
70 |
км |
на півгодини швидше, ніж зі швидкістю 60 |
км |
. Знайдіть цю |
||
|
|
|||||
|
год |
|
|
|
год |
|
відстань.
Розв’язання:
Нехай хкм – відстань між двома станціями, тоді зі швидкістю 70 км , потяг проходить цю відстань за x годин; а зі
|
год |
|
|
|
|
|
|
|
|
1 |
70 |
|
||
швидкістю 60 |
км |
– за |
x |
годин. Отримаємо: |
x |
+ |
= |
x |
, звідси |
|||||
|
60 |
70 |
|
|
||||||||||
|
год |
|
6x + 210 |
|
7x |
|
2 |
60 |
|
|||||
|
|
|
|
|
= |
, |
|
|
|
|
|
|
||
|
|
|
420 |
|
|
|
|
|
|
|
||||
|
|
|
420 |
|
|
|
|
|
|
|
||||
19
6x + 210 = 7x,
x = 210.
Відповідь: відстань між двома станціями рівна 210 км.
Задача 4.
Пасажирський потяг протягом 3 год проходить на 10 км більше,
ніж товарний протягом 4 год. Швидкість товарного потяга на
менша від швидкості пасажирського. Знайдіть ці швидкості. Розв’язання:
Нехай швидкість пасажирського потяга дорівнює
тоді швидкість товарного потяга — (x − 20) км .
год
Протягом 3 годин пасажирський потяг пройде 3x км. Протягом 4 годин товарний потяг пройде 4(x − 20) км.
20 км год
х км , год
Складемо |
рівняння, |
виходячи |
|
з |
умов |
|
|
задачі: |
|||
3x − 4(x − 20) = 10. Розв'яжемо це рівняння: |
|
|
|
|
|
|
|
|
|||
|
3x − 4(x − 20) = 10, |
|
|
|
|
|
|
||||
|
3x − 4x + 80 = 10, |
|
|
|
|
|
|
||||
|
− x = −70, |
|
|
|
|
|
|
|
|
||
|
x = 70. |
|
|
|
|
|
|
|
|
||
Швидкість |
пасажирського потяга |
дорівнює |
70 |
|
км |
|
, тоді |
||||
|
|
||||||||||
|
|
|
|
|
|
|
|
год |
|||
швидкість товарного потяга дорівнює 70 |
км |
− 20 |
км |
= 50 |
км |
. |
|||||
|
|
|
|||||||||
|
|
|
год |
год |
|
|
год |
||||
Відповідь: швидкість пасажирського потяга дорівнює 70 км ,
год
швидкість товарного потяга дорівнює 50 км .
год
Задача 5.
Велосипедист їхав 2 год ґрунтовою дорогою і 1 год асфальтованою — всього 28 км. Знайдіть його швидкість на кожній ділянці дороги, якщо асфальтованою дорогою він їхав зі швидкістю
на 4 км більшою, ніж ґрунтовою.
год
20
