диплом / Задачі_фізичного_змісту_при_вивченні_математики_в_загальноосвітній_школі

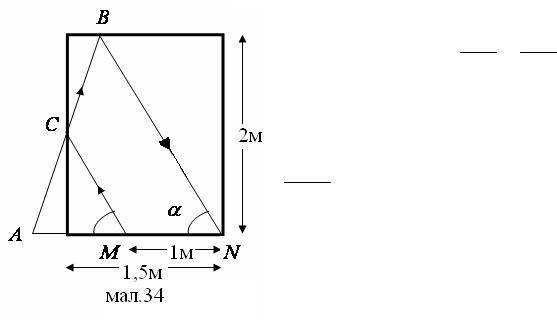
Відповідь: площі подібних трикутників пропорційні квадратам відповідних сторін).

Задача 4.

Більярдна куля знаходиться в точці М. Розміри більярдного столу подані на мал.16. Під яким кутом потрібно направити кулю, щоб попасти в лузу N відбиванням її від двох бортів? Рух кулі вважати рівномірним і що при ударі кут падіння дорівнює куту відбивання.

Розв’язання:

З подібності трикутників ABN і ACM випливає, що BN = AN ,

cosα

Відповідь: кулю потрібно направити під кутом α ≈ 63°, щоб попасти в лузу N відбиванням її від двох бортів.

161

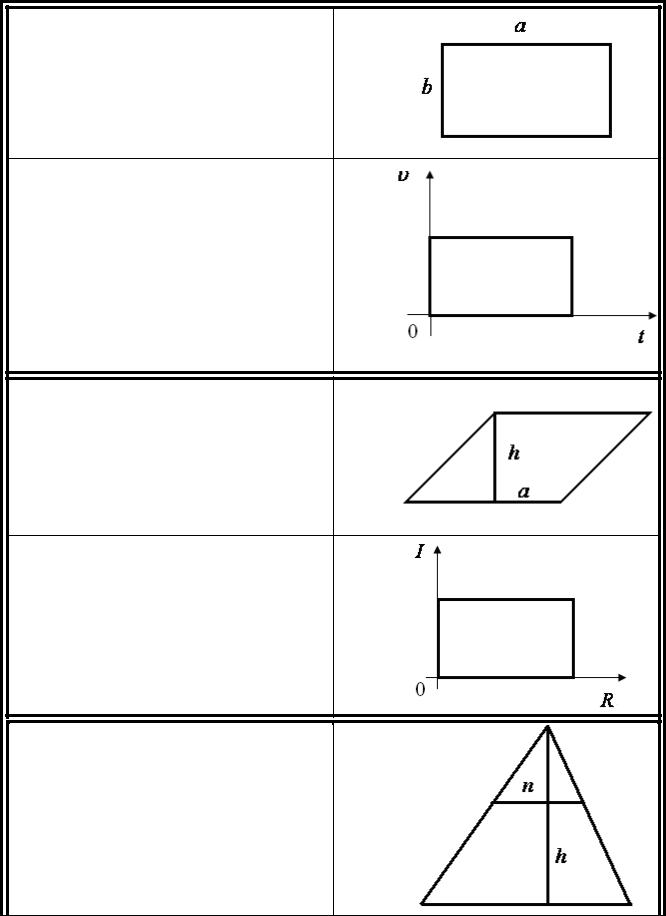
2.ПЛОЩІ МНОГОКУТНИКІВ

S = a ×b

S = υ ×t

S = a × h

U = I × R

S = n × h, де n— середня лінія трикутника

162

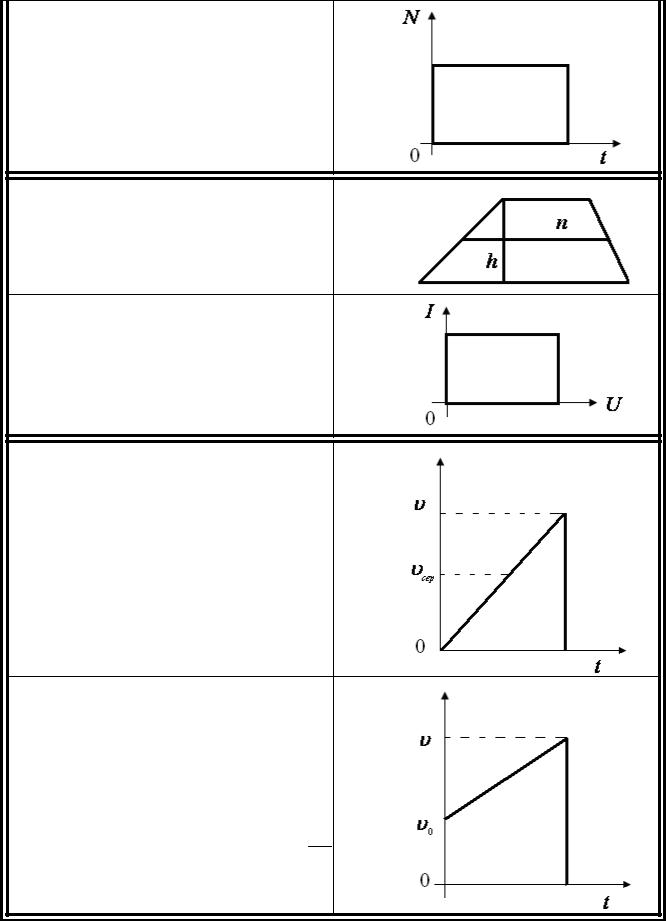
A = N ×t

S = n × h

P = U × I

S = υсер ×t;

163

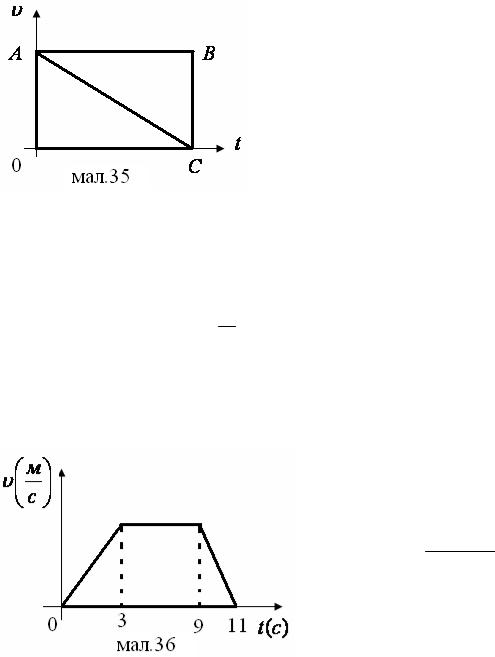
Задача1.

Від потяга, що рухається, на ходу відчіплюють останній вагон. Потяг продовжує рухатися з попередньою швидкістю, а останній вагон - рівносповільнено. Порівняйте шляхи, що пройшли потяг і вагон до моменту зупинки вагона.

Розв’язання:

Нехай до зупинки вагона минуло t секунд. Площа прямокутника ОАВС відповідає пройденому шляху, а площа трикутника ОАС – шляху, що пройшов вагон до зупинки (мал. 35).

Відповідь: Вагон пройшов шлях вдвічі менший за шлях потягу.

Задача 2.

Ліфт рівноприскорено піднімається протягом трьох секунд,

досягаючи швидкості 4 м. З цією швидкістю ліфт рухається 6с.

с

Останні дві секунди він рухається рівносповільнено. Визначте висоту підйому ліфта.

Розв’язання:

Висота підйому ліфта дорівнює площі трапеції:

h = S = 11с + 6с × 4м = 34м. 2

Відповідь: висота підйому ліфта 34 м.

164

Задача 3.

Автомобіль рухається рівноприскорено зі швидкістю υ0 = 0 . На

першому кілометрі його швидкість зростає на 10 м , на другому— на

с

5 м. Скільки часу затрачено на проходження першого кілометра?

с

другого кілометра?

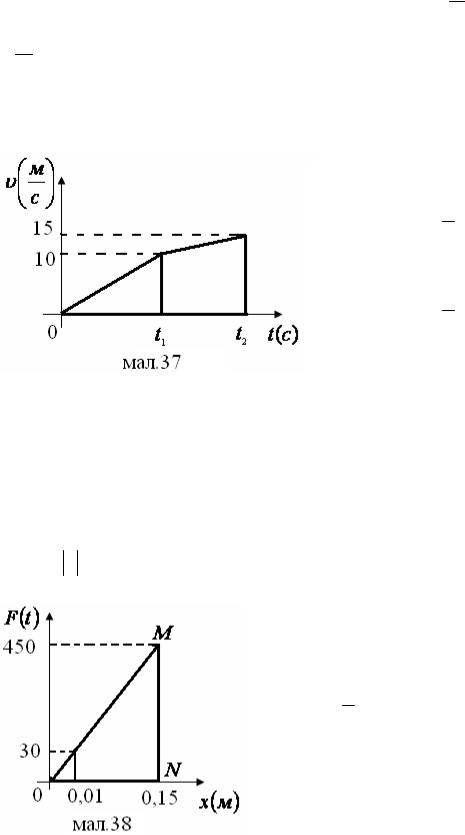
Розв’язання: (мал.37) 1км=1000м.

1000 = 1 t ×10,

2 1 t1 = 200.

1000 = 1 (15 +10)(t2 - t1 ), 2

t2 - t1 = 80.

Відповідь: на проходження першого кілометра затрачено200с, а на проходження другого кілометра затрачено 80с.

Задача 4.

Обчисліть роботу, виконану при стисненні пружини на 15 см, якщо відомо, що діюча сила пропорційна стисненню пружини і що для стиснення на 1 см необхідна сила 30 Н. (Задача на закон Гука

F = k × x ).

Розв’язання:

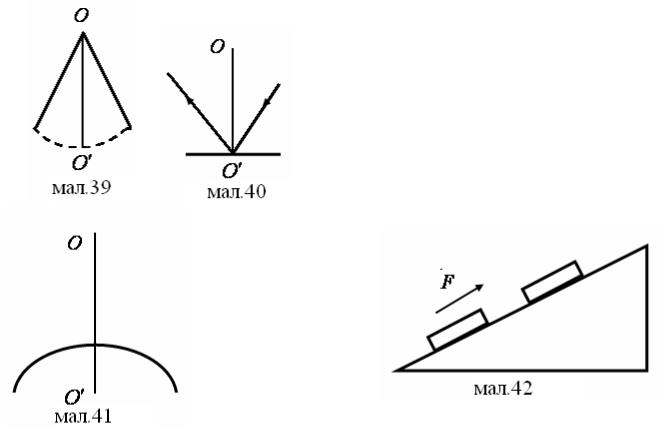
Величина шуканої роботи чисельно рівна площі трикутника OMN (мал.38).

Спосіб 1.

А= 1 × 0,15м× 450Н = 33,75 кДж 2

Спосіб 2.

165

Відповідь: робота, виконана при стисненні пружини, рівна

33,75Дж.

166

3.ПЕРЕМІЩЕНЯ ТА ЙОГО ВЛАСТИВОСТІ

В геометрії рухом називають перетворення площини (простору) зі збереженням розмірів і форми фігури. В геометрії ми розглядаємо лише початкове і кінцеве положення фігури. Рух в механіці— це безперервний процес з урахуванням ряду характеристик (швидкість, прискорення, сила, маса і ін.). (В більш широкому розумінні рух – це

довільна зміна в просторі і часі.).

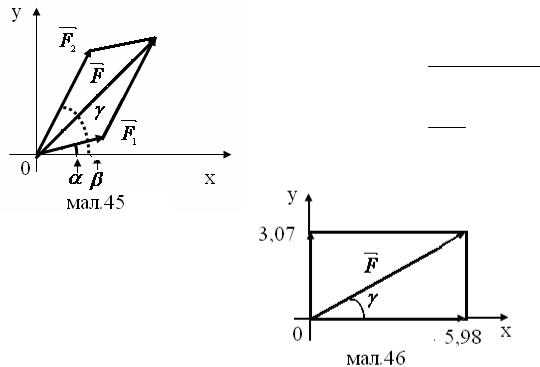
Розглянемо три приклади осьової симетрії (мал.39-

41):

Коливання маятника (мал.39).

Відбивання світла і звуку (мал.40).

Траєкторія тіла, кинутого під кутом до горизонту (мал.41)

Паралельне

перенесення можна розглядати як деяку абстракцію поступального руху. При поступальному

русі всі точки тіла описують однакові траєкторії, а пряма, що з’ єднує довільні дві точки тіла, переміщується згідно свого початкового напрямку.

Можна розглядати рух тіла по похилій площині як приклад поступального руху(мал.42).

Задача 1.

Годинникова і хвилинна стрілки співпадають опівночі. О котрій годині нового дня вперше знову співпадуть годинникова і хвилинна стрілки?

167

Розв’язання:

Дійсні повороти пов’язані з обертальним рухом твердого тіла і рухом по колу.

Кутова швидкість хвилинної стрілки в 12 раз більша, ніж кутова швидкість годинникової стрілки (мал.43):

ϕ1 = 2π - кут повороту

11

годинникової стрілки,

ϕ 2 = 2π + 2π - кут

11

повороту хвилинної стрілки.

Відповідь: приблизно о 1год5хв30снового дня вперше знову співпадуть годинникова і хвилинна стрілки.

Задача 2.

З якою швидкістю повинен летіти літак з заходу на схід на екваторі і на широті 60°, щоб пасажирам цього літака Сонце здавалося нерухомим на небі?

Розв’язання:

Удавана нерухомість Сонця досягається при рівності швидкостей руху літака і Землі

(мал.44):

Відповідь: літак повинен летіти зі швидкістю » 460 м з заходу

с

на схід на екваторі; а на широті 60° зі швидкістю » 230 м , щоб у

с

обох випадках пасажирам цього літака Сонце здавалося нерухомим на небі.

168

Задача 3.

Маховик, що затримується гальмом, за t c повертається на кут ϕ (t) = 4t − 0,3t 2 (радіан). Визначте:

а) кутову швидкість обертання маховика в момент часу t = 2c; б) в який момент часу маховик перестане обертатись?

Розв’язання:

При рівномірному русі по колу ω = ϕ , при нерівномірному - t

ω = ϕ ′(t).

а) ω = 4 - 0,6t, ϕ ′(2) = 4 - 0,6 × 2 = 2,8.

б) припинення обертання маховика відповідає значенню ω = 0, тобто

4 − 0,6t = 0, t = 6 2 . 3

169

4.ВЕКТОРИ

Всі фізичні величини діляться на скалярні (робота, шлях, час, сила струму, напруга і ін.) і векторні (швидкість, прискорення, переміщення, сила, напруженість електричного поля і ін.).

Розрізняють вільні і зв’язані вектори.

Вільні вектори (швидкість, прискорення і ін.) визначаються лише числовим значенням і напрямом.

Зв’язані вектори (сила і ін.) – числовим значенням, напрямом і точкою прикладання. При паралельному перенесенні зв’язаного вектора отримуємо інший вектор. Зі сказаного випливає, що сили і інші зв’язані вектори можна додавати лише тоді, коли вони прикладені до однієї точки.

Задача 1.

Додайте сили F1 = 3H i F2 = 4H , що утворюють з віссю ОХ кути α = 10° i β = 40°. Визначте кут між рівнодійною силою і віссю ОХ

(мал.45, мал.46).

Розв’язання:

Ox : 3cos10° + 4cos 40° ≈ 5,98;

Oy : 3sin10° + 4sin 40° ≈ 3,07;

F = 5,982 + 3,072 ≈ 6,8;

tgγ = 3,07 ≈ 0,51, 5,98

γ ≈ 27°.

Відповідь: рівнодійна сила F=6,8 Н, а кут між рівнодійною силою і віссю ОХ становить γ ≈ 27° .

170