диплом / Задачі_фізичного_змісту_при_вивченні_математики_в_загальноосвітній_школі

12,75 км , а потім на мотоциклі з швидкістю 67,5 км . Скільки часу

хв їхав на велосипеді.

2) 70,5 − 34 = 36,5(км)— відстань, яку він проїхав на мотоциклі за рахунок великої швидкості.

5)2 2 - 2 = 2(год) — листоноша їхав на велосипеді. 3 3

Відповідь: листоноша їхав 2 год на велосипеді і 2 год на

3

мотоциклі.

Задача 142.

Пішохід і велосипедист відправляються одночасно і по одній дорозі із міста А в місто В, яка знаходиться в 70 км від А. Пішохід йде

ними буде відстань, рівна 30 км, і яку відстань до В залишиться тоді проїхати велосипедисту і пройти пішоходу?

Розв’язання:

велосипедистом і пішоходом буде 30 км.

3)15 × 2 2 = 40(км) — проїхав велосипедист. 3

4)70 − 40 = 30(км)— залишилось проїхати велосипедисту.

141

5) 30 + 30 = 60(км) — залишилось пройти пішоходу.

Відповідь: відстань 30 км між велосипедистом і пішоходом буде

через 2 2 год; велосипедисту залишиться проїхати 30 км, а пішоходу

3

пройти 60 км.

Задача 143.

Почтовий потяг вийшов з станції о 7 год 25 хв ранку і йшов з

швидкістю 40,5 км . О 8 год 7 хв в тому ж напрямі відправився з цієї

год

станції швидкий потяг. З якою швидкістю повинен йти швидкий потяг, щоб наздогнати поштовий на відстані 210,6 км від станції?

швидкий потяг був менше часу в дорозі, чим поштовий.

3) 5,2 - 0,7 = 4,5(год) — стільки часу потрібно швидкому потягу, щоб пройти 210,6 км.

Відповідь: швидкість швидкого потяга рівна 46,8 км .

год

Задача 144.

На проходження шляху між двома пристанями теплоходу

потрібно на 40 хв більше, ніж катеру. Швидкість катера 40 км , а

год

теплохода — 30 км . Знайдіть відстань між пристанями.

год

3)20 :10 = 2(год) — за цей час катер пройде всю відстань.

4)40 × 2 = 80(км) — відстань між пристанями.

142

IIспосіб:

1)Теплохід проходить 1 км за 1 год = 2хв.

30

2) Катер проходить 1 км за 1 год = 1,5хв. 40

3) Теплоходу на 1 км шляху потрібно на 2 −1,5 = 0,5(хв) більше, ніж катеру, а на весь шлях на 40 хв більше.

4) Отже, весь шлях між пристанями 40 : 0,5 = 80(км) Відповідь: відстань між пристанями 80 км.

Задача 145.

О 8 год 30 хв ранку із двох пунктів виходять два автомобілі в одному напрямку. Автомобіль, який йде позаду, проходить всю

відстань між двома пунктами відправлення за 2 1 год, автомобіль, що

5

попереду, рухається в 216 разів повільніше того, що позаду. Коли

17

другий автомобіль наздожене перший? Розв’язання:

першого наздожене другий.

Відповідь: другий автомобіль наздожене першого об 11 год 50

хв.

Задача 146.

Два спортсмени змагалися в бігу на одну й ту ж відстань. Стартували вони в один й той же момент із одного пункту. Один

143

пробіг всю дистанцію за 1 хв 15 с, а другий за 1 хв 20 с. Скільки метрів за хвилину в середньому пробіг кожен спортсмен, якщо через 48 с після старту між ними була відстань 20 м?

Розв’язання:

1)1:1 1 = 4 всієї дистанції проходить перший спортсмен за 1 хв. 4 5

2)1:11 = 3 всієї дистанції проходить другий спортсмен за 1 хв. 3 4

другого спортсмена 375 м .

хв

Задача 147.

Відстань між пристанями на річці 43,2 км. Моторний човен, йдучи за течією річки, витрачає на цей шлях 2 год 24 хв. Скільки часу витрачає цей човен на цей же шлях, йдучи проти течії, якщо

швидкість течії 1,8 км ?

год

Розв’язання:

1) 43,2км: 2,4год = 18 км — швидкість моторного човна за

год

течією.

144

2) 18 км -1,8 км × 2 =14,4 км — швидкість човна проти течії.

год год год

3) 43,2км:14,4 км = 3год— витратить човен на цей же шлях,

год

йдучи проти течії.

Відповідь: 3 год витратить човен на шлях, йдучи проти течії.

Задача 148.

Теплохід, йдучи проти течії річки, пройшов відстань між пристанями за 9 год. Скільки часу потрібно теплоходу на зворотній шлях, якщо відстань між пристанями рівна 113,4 км, а швидкість течії

річки 1,9 км .

год

Розв’язання:

1) 113,4км: 9год =12,6 км — швидкість теплохода проти течії.

год

2) 12,6 км +1,9 км × 2 =16,4 км — швидкість теплохода за

год год год

течією.

3) 113,4км:16,4 км » 7год— знадобиться теплоходу, щоб пройти

год

цю відстань за течією.

Відповідь: теплоходу потрібно 7 год на зворотній шлях.

Задача 149.

Велосипедист проїхав 5 шляху і ще 40 км і йому залишилось

7 0,75 шляху без 118 км. Яка довжина шляху?

Розв’язання:

1) 1 - 5 = 2 всього шляху залишилось пройти, коли ще не були

7 7

пройдені 40 км.

2)3 - 2 = 13 всього шляху припадає на CD. 4 7 28

3)118 − 40 = 78(км) припадає на CD.

145

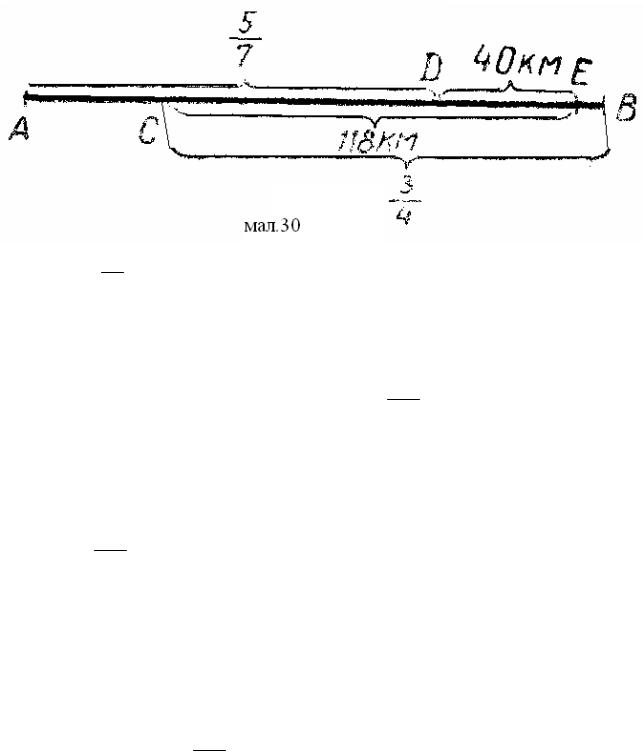
4) 78 : 13 = 168(км) — відстань від А до В. 28

Відповідь: відстань від А до В становить 168 км.

Задача 150.

Із міста А в місто В приїхали двоє товаришів. Один із них 4

години їхав на велосипеді з швидкістю 15 км і 6 годин на автомобілі.

год

Другий 3 години їхав на потязі і 2 години на автомобілі (швидкості автомобілів однакові). Швидкість автомобіля в 2 рази менша швидкості потяга. Чому дорівнює відстань від А до В?

Розв’язання:

1)15 км × 4год = 60км— проїхав перший товариш на велосипеді.

год

2)Другий товариш їхав 3 години на потязі, швидкість якого в 2

рази більша швидкості автомобіля, отже, за 3 години він пройшов таку ж відстань, що й перший за 6 годин на автомобілі.

А оскільки вони проїхали одну й ту ж відстань (від А до В), то, така відстань, яку проїхав перший на велосипеді,—60 км— другий проїхав на автомобілі за 2 години.

60км: 2год = 30 км — швидкість автомобіля.

год

Відповідь: відстань від А до В рівна 240 км.

146

Задача 151.

Потяг повинен був пройти відстань між пунктами А і В за 11 годин 15 хвилин. Вийшовши із пункту А, потяг спочатку рухався з меншою швидкістю і пройшов 0,4 всієї відстані за 5 годин. Але потім

збільшив швидкість на 10,8 км і прийшов в пункт В без запізнення.

год

Знайдіть відстань між пунктами А і В. Розв’язання:

1)11,25 - 5 = 6,25(год)— йшов потяг із збільшеною швидкістю.

2)1 − 0,4 = 0,6 всього шляху потяг йшов з збільшеною швидкістю.

3)0,6 : 6,25 = 0,096 всього шляху проходив потяг за годину після збільшення швидкості.

4)0,4 : 5 = 0,08 всього шляху проходив потяг за годину спочатку.

5)0,096 − 0,08 = 0,016 всього шляху складає 10,8 км.

6)10,8 : 0,016 = 675(км) — весь шлях.

Відповідь: відстань між пунктами А і В становить 675 км.

Задача 152.

Потяг повинен був пройти 720 км за 14 годин 24 хвилини. Пройшовши 0,75 цього шляху, він затримався із-за ремонту на 16 хвилин. З якою швидкістю потяг повинен продовжувати шлях, щоб прийти до місця призначення вчасно?

Розв’язання:

1)1 − 0,75 = 0,25 всього шляху залишилось пройти після зупинки.

2)720 × 0,25 = 180(км) залишилось пройти після зупинки.

3)14,4 × 0,25 = 3,6(год) повинен був їхати потяг останню чверть

шляху.

54 км , щоб прийти до місця призначення вчасно.

год

147

Задача 153.

Туристи здійснювали перехід на велосипедах три дні. За перший

день пройшли 1 всього шляху без 2 км. Другого дня— половину

3

шляху, що залишився, без 3 км і третього— 8 шляху, що залишився, і 9

ще додатково 6 км. Скільки кілометрів проїхали туристи за три дні? Розв’язання:

1)1 − 8 = 1 другого залишку складає 6 км. 9 9

2)6 : 1 = 54(км) — проїхали туристи третього дня. 9

3)54 − 3 = 51(км) — половина першого залишку.

4)51: 0,5 = 102(км)— перший залишок.

6) 100 : 2 = 150(км)— весь шлях. 3

Відповідь: туристи за три дні проїхали 150км.

Задача 154.

Після зустрічі двох теплоходів один з них пішов на північ, а другий на захід. Через дві години після зустрічі відстань між ними була 60 км. Знайдіть швидкість кожного теплохода, якщо відомо, що

швидкість одного з них була на 6 км більша швидкості другого.

год

перпендикулярні, то за теоремою Піфагора:

(2х)2 + [2(х + 6)]2 = 602 ,

148

18 + 6 = 24 км .

год

Відповідь: швидкість першого теплоходу становить 18 км , а

год

швидкість другого становить 24 км .

год

Задача 155.

Собака, знаходячись в точці А, побіг за лисицею, яка була на відстані 30 м від собаки. Стрибок собаки дорівнює 2 м, стрибок лисиці—1 м. Собака робить два стрибки за той час, як лисиця робить три стрибки. На якій відстані від точки А собака наздожене лисицю?

Розв’язання:

Два стрибки собаки складають 4 м; 3 стрибки лисиці складають 3м. Звідси, коли собака пробігає 4 м, відстань між собакою і лисицею зменшується на 4м - 3м = 1м. Початкова ж відстань між ними в 30 разів більша. Отже, собака наздожене лисицю, коли пробіжить

4м×30 = 120м.

Відповідь: собака наздожене лисицю на відстані 120 м від точки

А.

Задача 156.

Потяг вийшов з станції А на станцію С через В. Ділянку від А до В він йшов з встановленою швидкістю, а ділянку від В до С— із зменшеною на 25%. На зворотному шляху ділянку від С до В він йшов з встановленою швидкістю, а ділянку від В до А— з швидкістю, зменшеною на 25%. Скільки часу йшов потяг від А до С, якщо відомо, що на ділянку від А до В він затратив стільки ж часу, скільки на ділянку від В до С, і що на шлях в напрямку від А до С він

використав на 5 години менше, ніж на зворотній шлях (тобто від С

12

до А)?

Розв’язання:

Позначимо через t час руху потяга від А до С (в годинах) і через

149

зворотному шляху ділянку СВ було пройдено з швидкістю υ, а ділянку ВА— з швидкістю 0,75υ. Отже, ділянку СВ було пройдено за

0,75υt υ 0,75t υt υ

час : , тобто за год, а ділянку ВА— за : 0,75 , тобто за

звідки t = 10.

Відповідь: потяг йшов від А до С 10 годин.

Задача 157.

Велосипедисту потрібно було проїхати відстань в 30км. Виїхавши на 3 хв пізніше назначеного терміну, велосипедист їхав з

швидкістю, більшою на 1 км , і прибув вчасно на місце. Визначте

год

швидкість, з якою їхав велосипедист. Розв’язання:

Вважатимемо, що велосипедист їхав з швидкістю υ км ; тоді

год

швидкість, яка передбачалась, дорівнювала (υ -1) км . Фактично

умовою:

30- 30 = 3 ,

υ-1 υ 60

Звідки υ = 25 абоυ = −24.

Значення υ = −24 не задовольняє умову задачі.

Відповідь: швидкість, з якою їхав велосипедист, становить

25 км .

год

150