диплом / Задачі_фізичного_змісту_при_вивченні_математики_в_загальноосвітній_школі

Задача 80.

Коли повз пристань проплив пліт у село, яке лежить на відстані S1 = 15км від пристані, вниз за течією відплив моторний човен. Він доплив до села за t = 45хв і, повернувся назад, зустрів пліт на відстані S2 = 9км від села. Визначити швидкість течії річки и і швидкість υ човна відносно води.

Розв’язання:

У системі відліку, пов’язаній з берегом річки, човен проплив

тобто човен проти течії плив також 45хв. Для руху човна можна записати: (υ + u)t1 = S1 і (υ − u)t2 = S2 , звідки:

які рухаються з швидкостями υ. З якою швидкістю рухався потяг у Київ, якщо він зустрів ці електрички з інтервалом часу τ ?

Розв’язання:

год

частини цих рівностей, дістанемо:

u = υ t −τ τ .

Відповідь: потяг рухався у Київ зі швидкістю u = υ t −τ τ .

Задача 82.

З пункту А, розташованого на кільцевій трасі, одночасно стартують в тому самому напрямі велосипедист і мотоцикліст (обидва рухаються рівномірно). Поки велосипедист пройшов перше коло, мотоцикліст пройшов три повні кола і прийшов в пункт В, де

91

він обігнав велосипедиста перший раз. У скільки разів швидкість

мотоцикліст і який шлях він проїхав? Розв’язання:

Систему відліку доцільно пов’язати з колоною автомобілів. Від

Відповідь: мотоцикліст затратив 5,5 хв на відстань 5,25 км.

92

Задача 84.

Колона автомобілів виїжджає з певного пункту зі сталою

повертається в її хвіст, затративши на весь цей шлях t = 34хв. Визначити довжину колони, вважаючи, що вона не змінюється під час руху.

Розв’язання:

Пов’яжемо систему відліку з колоною. Мотоцикліст наздоганяє

третьего спортсмена, якщо спортсмени весь час знаходяться на одній прямій і пливуть по середині доріжок. Відстань між серединами першої і другої доріжок d1 , а між серединами другої і третьої d2 .

Розв’язання: Систему відліку

пов’яжемо з першим

93

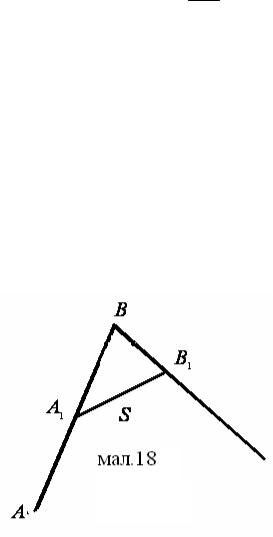
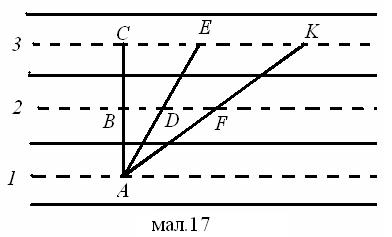
Нехай у певний момент часу спортсмени знаходяться в точках A, D і E. Через одиницю часу вони будуть у точках A, F і K ( перший спортсмен нерухомий у цій системі). Очевидно, що DF = υ1 + υ2 , а

Задача 86.

Два теплоходи рівномірно рухаються прямими курсами, які перетинаються під кутом α = 60°. Швидкості теплоходів однакові і

дорівнюють υ = 25 км . У початковий момент часу теплоходи

год

знаходилися в точках А і В, відстань між якими d = 50км. Визначити, через скільки часу відстань між теплоходами буде мінімальною і чому вона дорівнюватиме.

Розв’язання:

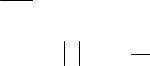
Нехай у якийсь момент часу t 0 теплоходи знаходяться в точках

A1 і B1 .

Smin = d sin α = 25 км. 2

Відповідь: через 1 годину відстань між теплоходами буде мінімальною і дорівнюватиме 25 км.

94

Задача 87.

Досягнувши швидкості υ0 = 108 км , автомобіль починає

год

рухатися рівносповільнено з прискоренням а = 0,4 м . Через який час

с2

його швидкість зменшиться в n = 3 рази? Розв’язання:

Швидкість автомобіля через час t після початку сповільнення

причому його швидкість в пункті В була в n = 5 разів більша, ніж в А.

Визначити швидкість мотоцикліста в пунктах А і В, час, затрачений

95

Відповідь: швидкість мотоцикліста в пункті А ≈ 8,33 м , в пункті

с

В≈ 41,6 м , відстань ОА≈ 5,2 м, час, затрачений на рух до цих пунктів

с

1,25 с і 6,25 с відповідно.

Задача 89.

Два велосипедисти їдуть назустріч один одному. Один з них,

рівноприскорено спускається з прискоренням а = 0,2 м . Через який

с2

час вони зустрінуться і яку відстань до зустрічі проїде кожен, якщо відстань між ними в початковий момент часу S0 = 130м?

Розв’язання:

За початок системи координат візьмемо початкове положення першого велосипедиста і вісь Ох спрямуємо в напрямку швидкості

Відповідь: два велосипедисти зустрінуться через 20 с і перший велосипедист проїде до зустрічі 60 м, а другий 70 м.

Задача 90.

Два автомобілі вирушили одночасно із села до міста, відстань між якими становить 180 км. Один автомобіль прибув до міста на 45

хв пізніше, ніж другий, оскільки його швидкість була на 20 км год

менша. 3 якою швидкістю рухався кожний автомобіль?

96

Корінь —80 не задовольняє умови задачі. Отже, перший

Відповідь: перший автомобіль рухався зі швидкістю 60 км , а

год

другий рухався зі швидкістю 80 км .

год

Задача 91.

Моторний човен пройшов 21 км проти течії річки і 8 км за течією, витративши на весь шлях 2 год. Знайдіть швидкість човна в

стоячій воді, якщо швидкість течії річки становить1 км .

год

97

течією. Оскільки на весь рух було затрачено 2 години, то маємо рівняння:

Значення х = - 1 не задовольняє умову задачі. 2

Відповідь: швидкість човна в стоячій воді становить 15 км .

год

Задача 92.

З міста А в місто В виїхав велосипедист. Через 3 год із міста А виїхав мотоцикліст, який прибув у місто В одночасно з велосипедистом. Знайдіть швидкість мотоцикліста, якщо вона на

45 км більша за швидкість велосипедиста, а відстань між містами А і год

В становить 60 км.

на 3 години довше, то маємо рівняння:

98

Відповідь: швидкість мотоцикліста становить 60 км .

год

Задача 93.

Перші 200 км дороги від А до В автомобіль проїхав із певною

швидкістю, а останні 150 км— зі швидкістю, на 20 км меншою.

год

Знайдіть швидкість автомобіля, з якою він проїхав останні 150 км, якщо на весь шлях від А до В він витратив 5 год.

Розв’язання:

Нехай х км — швидкість автомобіля, з якою він проїхав 150 км,

год

Оскільки на весь шлях було витрачено 5 годин, то маємо рівняння:

99

150(х + 20) + 200х - 5х(х + 20) =

0;

х(х + 20)

дорогою завдовжки 210 км, а повертався з пункту В в пункт А по ґрунтовій дорозі завдовжки 160 км, витративши на зворотний шлях на 1 год більше, ніж на шлях з пункту А в пункт В. З якою швидкістю

їхав автомобіль по ґрунтовій дорозі, якщо вона на 30 км менша, ніж

затрачений на поїздку з пункту В до пункту А. За умовою задачі,

100