
- •Структура умк дистанционного обучения учебной дисциплины
- •Рабочая программа
- •1. Цели и задачи дисциплины
- •1.1. Цель преподавания дисциплины.
- •1.2. Задачи изучения дисциплины.
- •Содержание и структура дисциплины
- •2.1. Лекции, их содержание и наименование тем
- •2.2. Лабораторные занятия
- •2.3. Практические занятия
- •Содержание самостоятельной работы студентов
- •1. Предмет и основные задачи эконометрики
- •1.1. Введение в предмет эконометрика
- •1.2. Основные этапы эконометрического исследования
- •2. Особенности построения эконометрических моделей
- •2.1. Обоснование формы эконометрической модели
- •2.2. Выбор факторов эконометрической модели
- •3. Множественная линейная регрессия
- •3.1. Анализ множественной линейной регрессии с помощью
- •3.2. Теоретические предпосылки мнк
- •3.3. Оценивание коэффициентов множественной
- •3.4. Интерпретация оценок параметров и уравнения
- •4. Анализ качества уравнения регрессии
- •4.1. Характеристики и критерии качества эконометрических
- •4.2. Дисперсии и стандартные ошибки параметров линейной регрессии
- •4.3. Доверительные интервалы коэффициентов регрессии
- •4.4. Стандартная ошибка и доверительные интервалы уравнения регрессии
- •4.5. Статистическая значимость уравнения регрессии
- •5. Уравнение регрессии в стандартизованной форме
- •5.1. Стандартизованные переменные
- •5.2. Нормальная система уравнений мнк в стандартизованных
- •5.3. Параметры стандартизованной регрессии
- •6. Возможности экономического анализа на основе многофакторной модели
- •6.1. Коэффициенты стандартизованной регрессии
- •6.2. Средние и частные коэффициенты эластичности
- •6.3. Линейные коэффициенты парной, частной и
- •Варианты контрольных заданий Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Порядок выполнения типового примера.
- •Вопросы к зачету по дисциплине «эконометрика»
- •6. Нелинейная регрессия
6.2. Средние и частные коэффициенты эластичности
В экономических
исследованиях для количественного
представления результатов множественного
анализа также часто применяют коэффициенты
эластичности. Коэффициент эластичности
характеризует изменение в процентах
объясняемой переменной при изменении
факторной переменной на 1% и определяется
для зависимости
![]() как
как
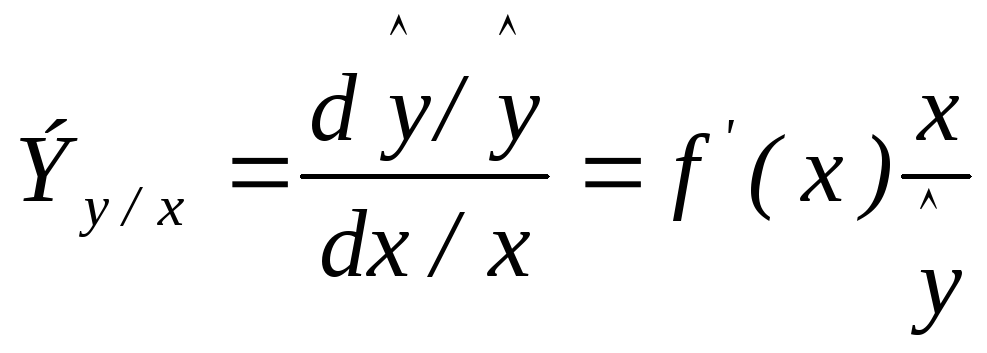 .
.
Он имеет четкую
экономическую интерпретацию для
степенной функции
![]() .
Производная этой функции
.
Производная этой функции![]() .
Оказывается, что коэффициент эластичности
при этом равен
.
Оказывается, что коэффициент эластичности
при этом равен
![]()
и имеет постоянную величину.
Обобщение понятия
эластичности на другие формы регрессионной
связи приводит к тому, что
![]() оказывается зависящим от величины
факторной переменной. Так для линейной
регрессии
оказывается зависящим от величины
факторной переменной. Так для линейной
регрессии![]() эластичность принимает вид:
эластичность принимает вид:
![]() .
.
Поскольку коэффициент эластичности для линейной функции не является постоянной величиной, то вводят средний показатель эластичности:
![]() .
.
Для характеристики относительной силы влияния каждого фактора в многофакторной регрессии используют частные коэффициенты эластичности:
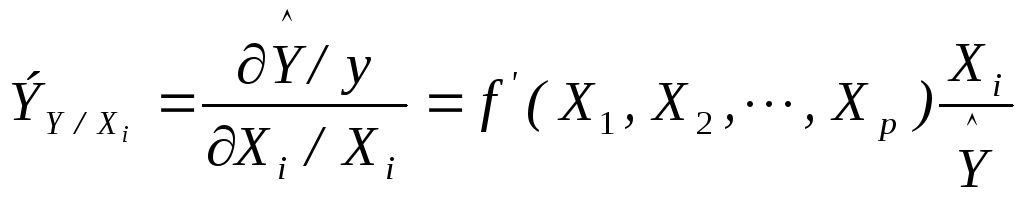
В частном случае двухфакторной линейной зависимости
![]()
для характеристики влияния Х1 и Х2 на Y рассчитывают частные коэффициенты эластичности:
![]() ,
,
![]() .
.
Экономическая
интерпретация этой статистической
взаимосвязи является следующей. При
увеличении фактора Х1
на 1% от его среднего уровня объясняемая
переменная Y
изменяется на
![]() ,%
своего от среднего уровня, а при увеличении
фактораХ2
на 1% от его среднего уровня объясняемая
переменная Y
изменяется
на
,%
своего от среднего уровня, а при увеличении
фактораХ2
на 1% от его среднего уровня объясняемая
переменная Y
изменяется
на
![]() ,%
от своего среднего уровня.
,%
от своего среднего уровня.
Направление изменения объясняемой переменной зависит от знака коэффициента при соответствующем факторе.
6.3. Линейные коэффициенты парной, частной и
множественной корреляции
Наиболее обоснованной
характеристикой статистической связи
является выборочный коэффициент линейной
корреляции. При исследовании двухфакторной
модели
![]() линейные
коэффициенты парной корреляции
определяются следующим:
линейные
коэффициенты парной корреляции
определяются следующим:
![]() ,
,
![]() ,
,
![]() .
.
Анализируя значения коэффициентов парной корреляции, приходим к выводам относительно силы и направления взаимосвязи между каждой парой переменных. Однако очевидно, что влияние каждой из факторных переменных на объясняемую переменную не может выражаться также просто, как в случае парной регрессии, в силу их взаимосвязи между собой.
Для характеристики влияния каждого фактора множественной регрессии, аналогичной стандартизованным коэффициентам регрессии, на основе парных коэффициентов линейной корреляции рассчитывают частные коэффициенты корреляции. Они также используются при отборе факторов: целесообразность включения того или иного фактора в модель можно обосновывать величиной показателя частной корреляции.
Частные коэффициенты
корреляции характеризуют влияние
фактора
![]() на объясняемую переменную
на объясняемую переменную![]() при устранении влияния других факторов,
включенных в уравнение регрессии. В
зависимости от их числа вычисляют
частные корреляции различного порядка.
при устранении влияния других факторов,
включенных в уравнение регрессии. В
зависимости от их числа вычисляют
частные корреляции различного порядка.
В случае двухфакторной модели частные коэффициенты корреляции первого порядка вычисляются непосредственно с помощью парных коэффициентов корреляции по формулам:
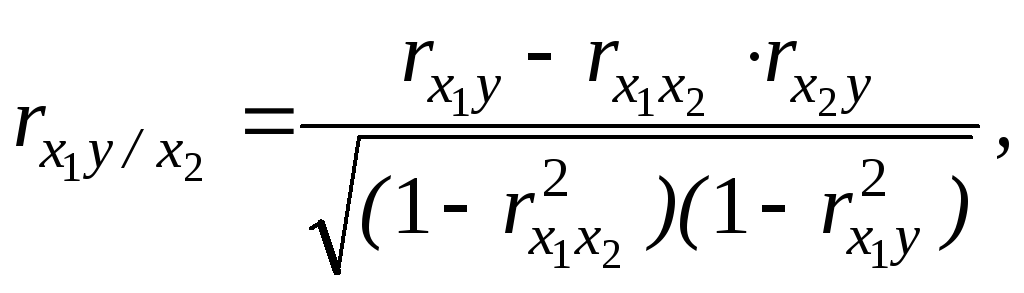
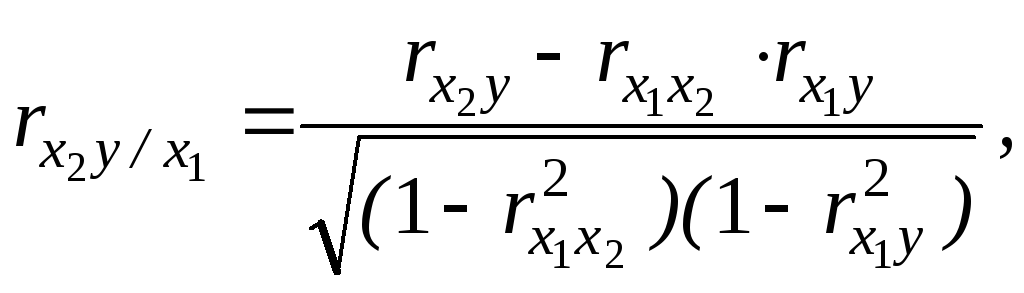
![]()
Если сравнить
значения коэффициентов парной и частной
корреляции, то приходим к выводу, что
из-за сильной связи
![]() и
и![]() ,
умеренной
связи
,
умеренной
связи
![]() и
и![]() коэффициенты
коэффициенты![]() и
и![]() отличаются незначительно,
отличаются незначительно,![]() и
и![]() - значительно. Выводы о направлении
связи на основе этих коэффициентов
совпадают.
- значительно. Выводы о направлении
связи на основе этих коэффициентов
совпадают.
Когда общее число
факторов больше двух и равно р,
то возможны частные коэффициенты
корреляции не только первого, но и
второго, третьего, …, (р-1)
порядка. Так
влияние фактора
![]() на переменнуюY
можно оценить при разных способах
исключения влияния других факторов: по
одному, по два, …, всех (р-2)
– ух факторов из числа входящих в
регрессию. Хотя частная корреляция
различного порядка и может представлять
интерес при изучении различных
взаимосвязей факторных переменных, на
практике ограничиваются вычислением
частных корреляций самого высокого
порядка. Этими показателями обычно
принято дополнять эмпирические модели
множественной регрессии
на переменнуюY
можно оценить при разных способах
исключения влияния других факторов: по
одному, по два, …, всех (р-2)
– ух факторов из числа входящих в
регрессию. Хотя частная корреляция
различного порядка и может представлять
интерес при изучении различных
взаимосвязей факторных переменных, на
практике ограничиваются вычислением
частных корреляций самого высокого
порядка. Этими показателями обычно
принято дополнять эмпирические модели
множественной регрессии
Практическая
значимость эмпирического уравнения
множественной регрессии оценивается
помощью коэффициента множественной
корреляции
![]() или его квадрата
или его квадрата![]() – коэффициента множественной детерминации.
– коэффициента множественной детерминации.
Коэффициент множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с объясняемой переменной, или оценивает тесноту совместного влияния факторов на результат. Его величина не может быть меньше, чем величина наибольшего коэффициента парной корреляции:
![]() .
.
При правильном выборе факторов величина коэффициента множественной корреляции должен существенно отличаться от коэффициентов парной корреляции. Целесообразность включения в состав регрессии нового фактора можно обосновать, сравнивая коэффициенты множественной и парной корреляции с его участием.
Коэффициент множественной корреляции можно рассчитать несколькими способами, это полезно делать для контроля правильности вычислений:
1) наиболее просто это сделать для уравнения линейной регрессии в стандартизованной форме:
![]() .
.
2) используя матрицу парных коэффициентов корреляции:
![]() ,
,
где
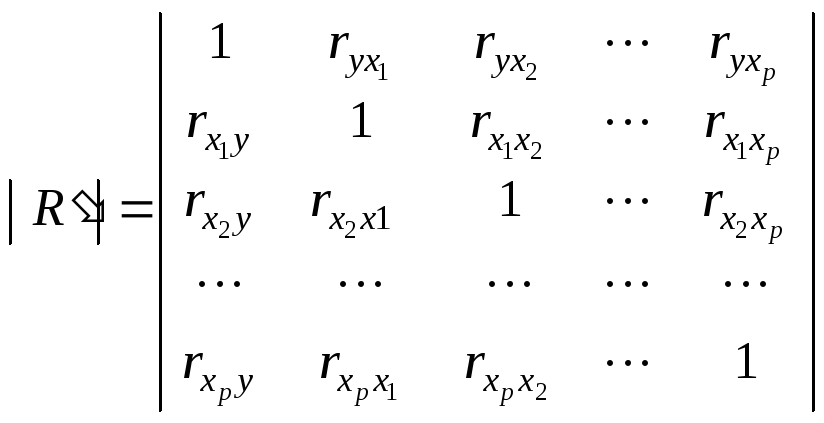 - определитель матрицы коэффициентов
парной корреляции;
- определитель матрицы коэффициентов
парной корреляции;
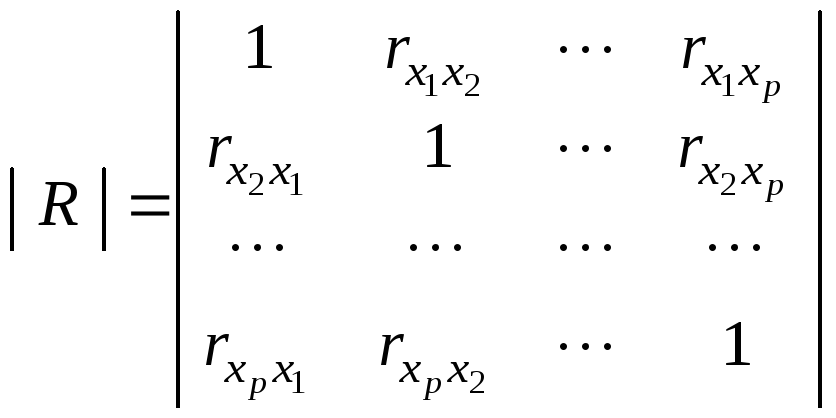 -
определитель матрицы коэффициентов
парной корреляции между факторами, или
межфакторного взаимодействия.
-
определитель матрицы коэффициентов
парной корреляции между факторами, или
межфакторного взаимодействия.
3) как корень квадратный из коэффициента множественной детерминации:
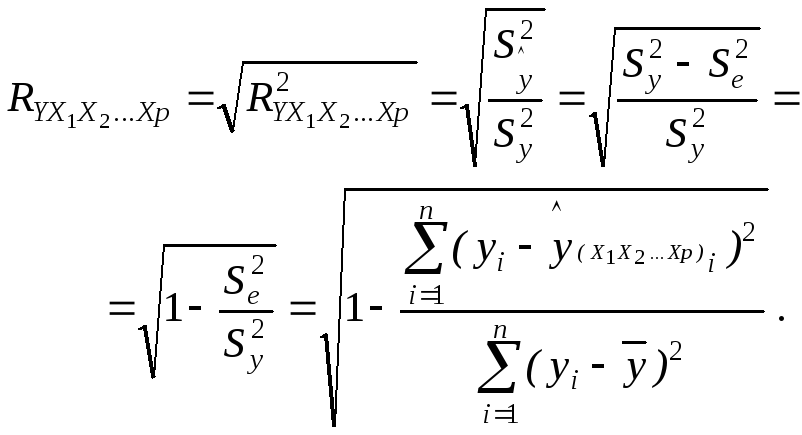
На основании значения коэффициента множественной регрессии делается вывод о том, что зависимостью переменной у от факторных переменных объясняется R2*100 % вариации, представленной исходными данными. Прочие факторы, не включенные в модель, составляют соответственно ( 1- R2)*100% от общей вариации объясняемой переменной у.
