
- •Часть 1
- •Набережные Челны
- •Введение
- •Цели и задачи дисциплины
- •Общие методические указания
- •Структура и содержание дисциплины «физика»
- •Раздел 1. Физические основы механики
- •Тема 1.1. Элементы кинематики
- •Тема 1.2. Элементы динамики частиц
- •Тема 1.3. Законы сохранения в механике
- •Тема 1.4. Элементы механики твердого тела
- •Тема 2.3. Ангармонические колебания
- •Тема 3.3. Функциираспределения
- •Тема 3.4. Элементы физической кинетики
- •Тема 3.5. Распределение Гиббса
- •Тема 3.6. Порядок и беспорядок в природе
- •Раздел 4. Электричество и магнетизм
- •Тема 4.1. Электростатика
- •Тема 4.2. Постоянный электрический ток
- •Форма и содержание итогового контроля
- •Методические указания
- •К выполнению контрольной работы № 1
- •Физические основы механики, механические колебания и волны.
- •Основные законы и формулы
- •Примеры решения задач
- •Контрольная работа №1
- •Методические указания
- •К выполнению контрольной работы № 2
- •Статистическая физика и термодинамика
- •Основные законы и формулы
- •Примеры решения задач
- •Контрольная работа № 2
- •Методические указания к выполнению контрольной работы № 3 Электростатика, постоянный ток Основные законы и формулы
- •Примеры решения задач
- •Контрольная работа № 3
- •1. Основные физические постоянные
- •2. Некоторые астрономические величины
- •Часть 1
Примеры решения задач
Пример 1.
В вершинах квадрата находятся одинаковые
точечные заряды
![]() Какой отрицательный заряд
Какой отрицательный заряд![]() надо поместить в центре квадрата, чтобы
указанная система зарядов находилась
в равновесии?
надо поместить в центре квадрата, чтобы
указанная система зарядов находилась
в равновесии?
Решение:
Все заряды, расположенные в вершинах
квадрата, находятся в одинаковых
условиях. Поэтому достаточно выяснить,
какой заряд следует поместить в центр
квадрата, чтобы какой-нибудь из четырёх
зарядов, например
![]() ,
находился в равновесии. Заряд
,
находился в равновесии. Заряд![]() будет находиться в равновесии, если
векторная сумма действующих на него
сил равна 0 (рис. 1):
будет находиться в равновесии, если
векторная сумма действующих на него
сил равна 0 (рис. 1):
![]() (1)
(1)
где
![]() силы, с которыми соответственно
силы, с которыми соответственно
q2 q3



q5


![]()
![]()

q4 q1








![]()
![]()
![]()
Рис 1.
действуют на заряд
![]() ,
заряды
,
заряды![]()
![]() равнодействующая
сил
равнодействующая
сил![]() и
и![]() .
.
По закону Кулона,
имея в виду, что
![]() получим
получим
 (2)
(2)
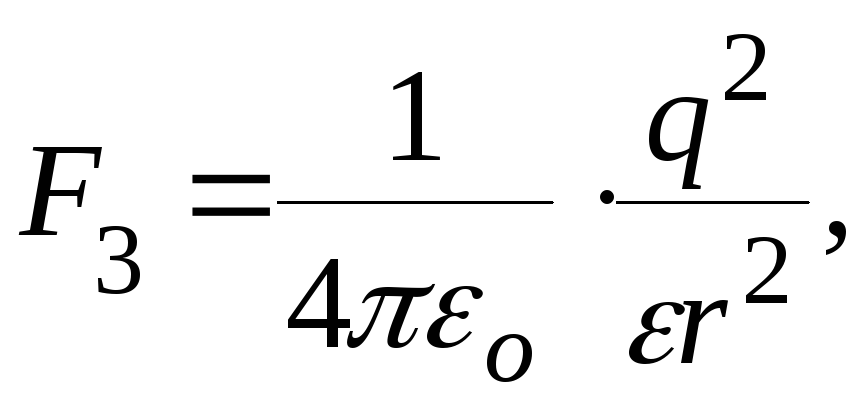 (3)
(3) (4)
(4)
где а – сторона
квадрата, r=а![]() - диагональ квадрата. Равнодействующая
сил
- диагональ квадрата. Равнодействующая
сил![]() и
и![]() как следует из рис. 1, по направлению
совпадает с силой
как следует из рис. 1, по направлению
совпадает с силой![]() и по модулю равна
и по модулю равна
![]() С учётом этого
векторное равенство (1) можно заменить
скалярным:
С учётом этого
векторное равенство (1) можно заменить
скалярным:
![]() .
(5)
.
(5)
Равенство (5) с учётом (2)-(4) примет вид:
 ,
,
Откуда
![]() .
.
Произведём вычисления:
![]()
Следует отметить, что равновесие системы зарядов будет неустойчивым.
Пример 2.
Тонкий прямой стержень длиной
![]() равномерно заряжен с линейной плотностью
заряда
равномерно заряжен с линейной плотностью
заряда![]() На продолжении оси стержня, на
расстоянии а=20см от ближайшего конца,
находится точечный заряд
На продолжении оси стержня, на
расстоянии а=20см от ближайшего конца,
находится точечный заряд![]() Определить силу взаимодействия стержня
и точечного заряда.
Определить силу взаимодействия стержня
и точечного заряда.
Решение. Так как стержень не является точечным зарядом, то закон Кулона непосредственно применить нельзя.
dr
r
q1




a![]()








Рис. 2
Разобьем стержень
на малые элементы и выделим на стержне
(рис. 2) элемент dr
c
зарядом
![]() .
Этот заряд можно рассматривать как
точечный. Тогда по закону Кулона
.
Этот заряд можно рассматривать как
точечный. Тогда по закону Кулона
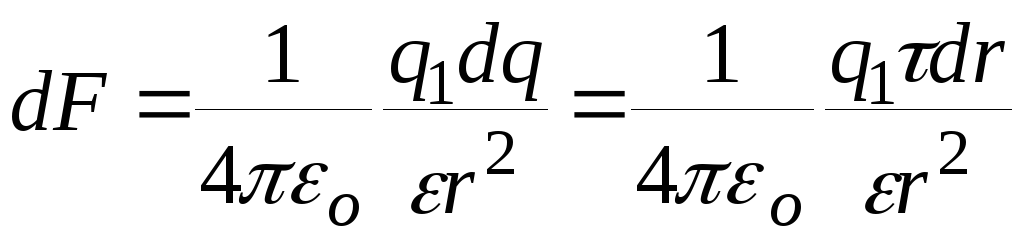 . (1)
. (1)
Силу взаимодействия точечного заряда и стержня с учётом принципа суперпозиции найдём интегрированием выражения (1)
 Проверим,
даёт ли расчётная формула единицу силы.
Для этого в правую часть формулы вместо
символов величин подставим их единицы
измерений:
Проверим,
даёт ли расчётная формула единицу силы.
Для этого в правую часть формулы вместо
символов величин подставим их единицы
измерений:

Выразим все величины
в единицах СИ:
![]() ,
,![]() ,
а=0,2м,
,
а=0,2м,![]() =10
=10![]() Кл/м,
Кл/м,![]() ,
,![]() м/Ф.
м/Ф.
Произведём вычисления:
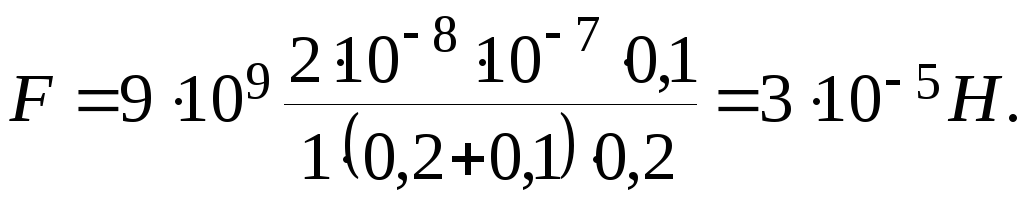
Пример 3.
Два точечных заряда
![]() =2
нКл и
=2
нКл и![]() =
-1 нКл находятся в воздухе на расстоянииd
= 5 см друг от друга. Определить напряжённость
=
-1 нКл находятся в воздухе на расстоянииd
= 5 см друг от друга. Определить напряжённость
![]() и потенциал
и потенциал![]() поля в точке, удалённой от заряда
поля в точке, удалённой от заряда![]() на расстояниеr1
=6 см и от
заряда
на расстояниеr1
=6 см и от
заряда
![]() наr2
=4 см.
наr2
=4 см.
Решение:
Согласно
принципу суперпозиции электрических
полей каждый заряд создаёт поле
независимо от присутствия в пространстве
других зарядов. Напряжённость
результирующего поля
![]() .
Напряжённости поля, создаваемого в
воздухе
.
Напряжённости поля, создаваемого в
воздухе![]() зарядами
зарядами![]() и
и![]() .
.

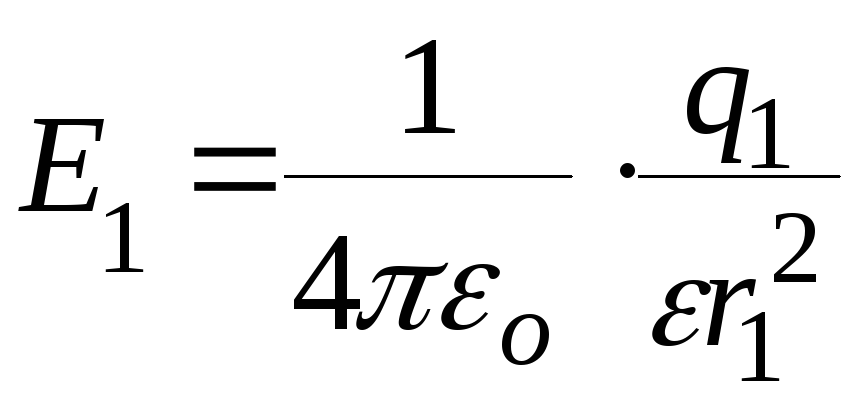 ,
(1)
,
(1)
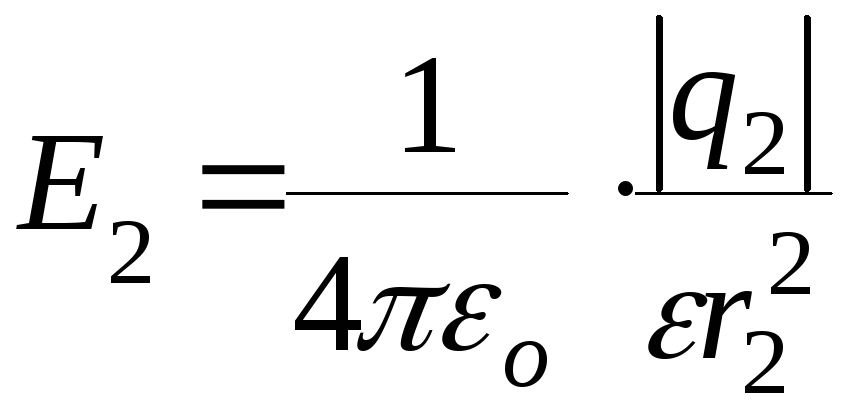 .
(2)
.
(2)
Направления
векторов
![]() и
и![]()
указаны на рис.
3вектора
![]() найдём по теореме косинусов:
найдём по теореме косинусов:
Рис. 3
![]() , (3)
, (3)
где
![]() -
угол между векторами
-
угол между векторами![]() и
и![]() .
Из рис.3 видно, что
.
Из рис.3 видно, что![]() .
Тогда
.
Тогда![]() .
.
Следовательно,
![]() (4)
(4)
Из треугольника
со сторонами r1,
r2
и d
по теореме косинусов находим
![]()
Вычислим
![]() отдельно:
отдельно:
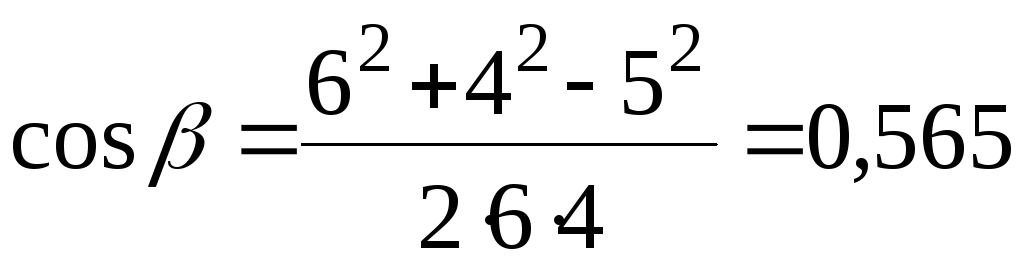 .
.
По принципу
суперпозиции потенциал результирующего
поля, создаваемого зарядами
![]() и
и![]() равен алгебраической сумме потенциалов
равен алгебраической сумме потенциалов![]() и
и![]() т.е.
т.е.![]() ,
или
,
или
 .
(5)
.
(5)
Выразим все величины в единицах СИ:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Произведём вычисления по формулам (1), (2), (4), (5):

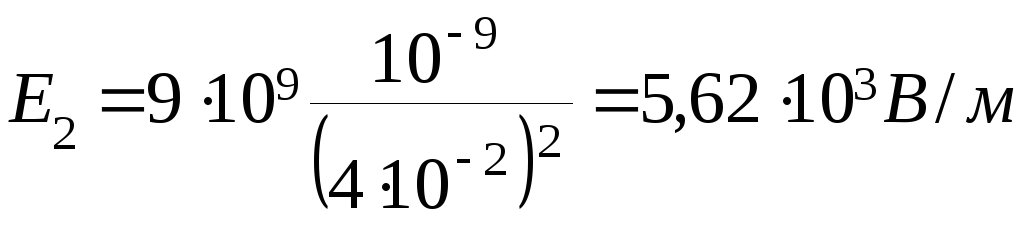 .
.
При вычислении Е2
знак заряда q2
опущен, так
как знак минус определяет направление
вектора
![]() ,
а направление
,
а направление![]() было учтено при его графическом
изображении (рис. 3)
было учтено при его графическом
изображении (рис. 3)
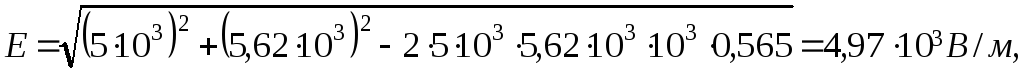
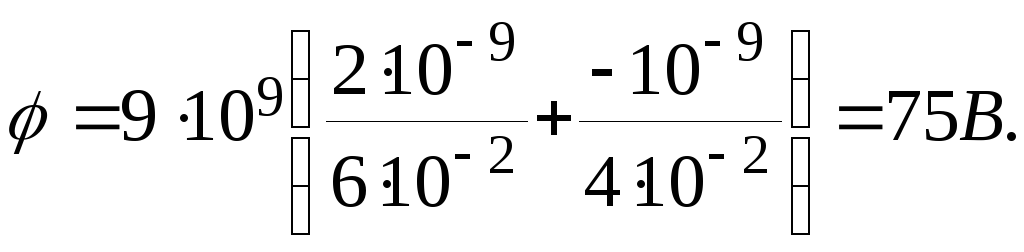
Пример 4.
По тонкой нити, изогнутой по дуге
окружности радиусом R=6
см, равномерно распределён заряд с
линейной плотностью
![]() =20
нКл/м. Определить напряжённость Е и
потенциал
=20
нКл/м. Определить напряжённость Е и
потенциал![]() электрического поля, создаваемого
распределённым зарядом в точке,
совпадающей с центром кривизны дуги,
если длина нити составляет 1/3 длины
окружности.
электрического поля, создаваемого
распределённым зарядом в точке,
совпадающей с центром кривизны дуги,
если длина нити составляет 1/3 длины
окружности.
Решение.
Выберем оси координат так, чтобы начало
координат совпадало с центром кривизны
дуги, а ось OY
была бы расположена симметрично
относительно концов дуги (рис. 4). Разобьем
нить на элементарные участки и
выделим элемент длиной
![]() c
зарядом
c
зарядом
![]() .
Этот заряд можно р
.
Этот заряд можно р ассматривать
как точечный.
ассматривать
как точечный.
Определим напряжёность элетрического поля в точке О. Для этой точки напряжённость поля,
Рис. 4 создаваемого
зарядом
![]() dq,
равна
dq,
равна
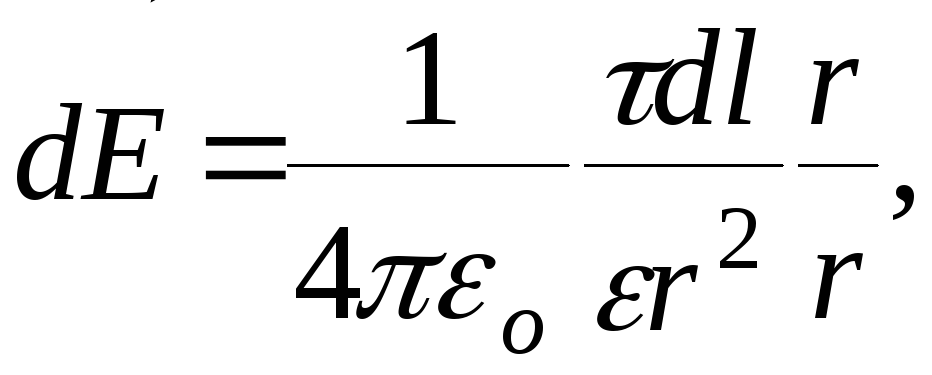
где
![]() -
радиус- вектор, направленный от элемента
-
радиус- вектор, направленный от элемента![]() в точку О. Разобьем вектор
в точку О. Разобьем вектор![]() на составляющие
на составляющие![]() и
и![]() .
Из симметрии задачи следует, что сумма
составляющих
.
Из симметрии задачи следует, что сумма
составляющих![]() от всех элементарных участков нити
равна нулю и
от всех элементарных участков нити
равна нулю и
результирующий
вектор
![]() направлен вдоль осиOY.
Поэтому напряжённость поля определится
как
направлен вдоль осиOY.
Поэтому напряжённость поля определится
как
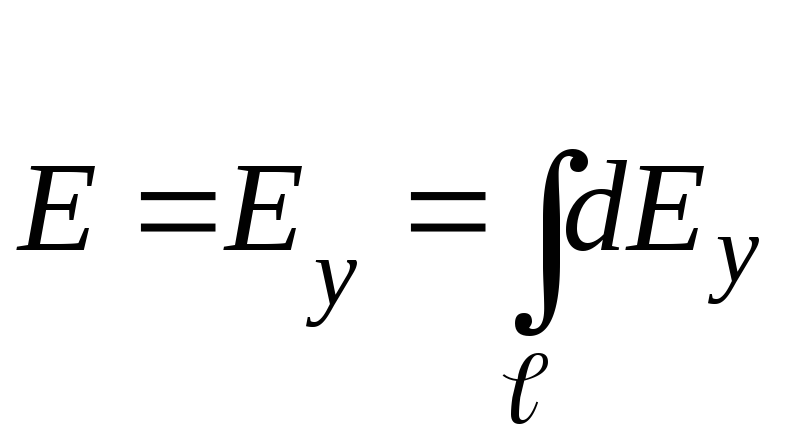 ,
(1)
,
(1)
где
![]() .
Так как
.
Так как
![]() и
и
![]() ,
,
то
 .
(2)
.
(2)
Подставив выражение (2) в (1), получим
 (3)
(3)
Найдём потенциал
электрического поля в точке О. В этой
точке потенциал поля, созданного
точечным зарядом
![]() ,
равен
,
равен
 (4)
(4)
Потенциал
результирующего поля получим
интегрированием выражения (4)
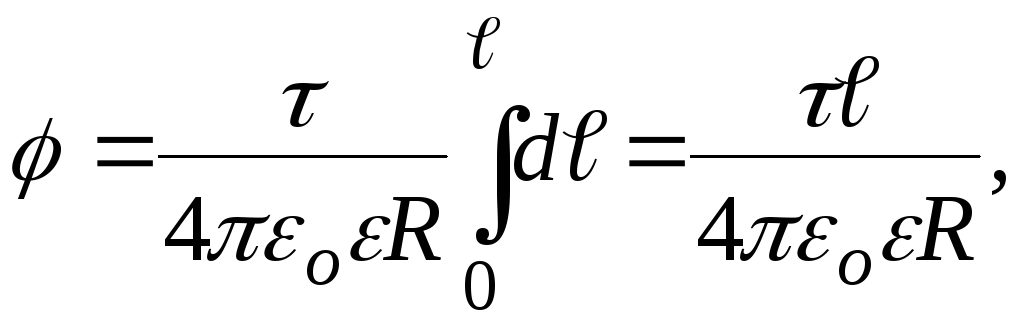
Так как,
![]() то
то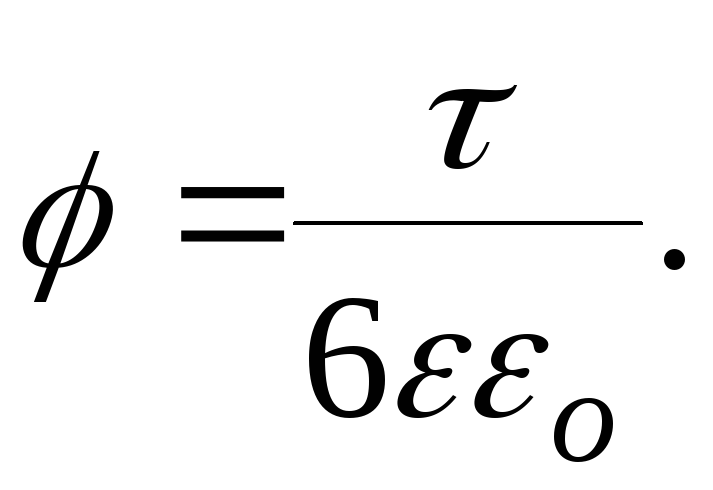 (5)
(5)
Выразим все величины
в единицах СИ:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
Произведём вычисления по формулам (3) и (5):
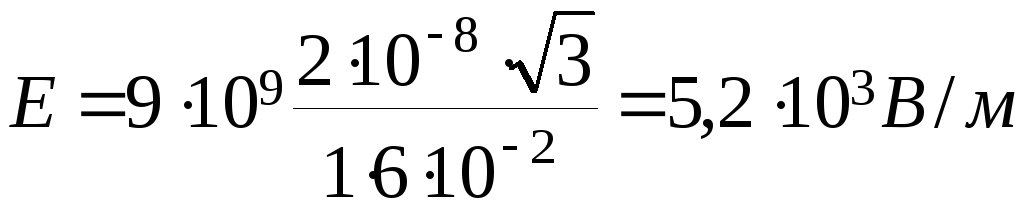 ,
,
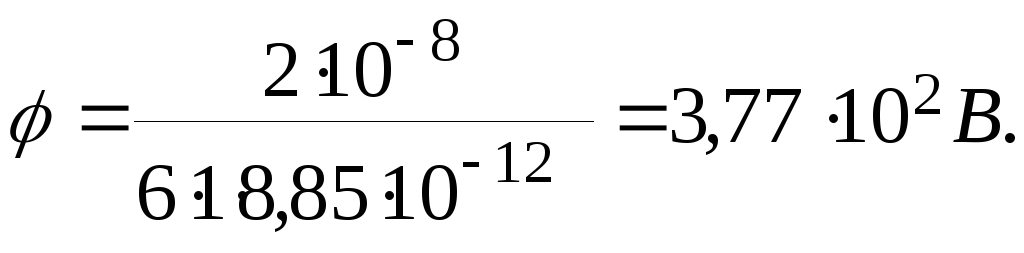
Пример 5.
Электрическое
поле создано длинным цилиндром радиусом
R=1см,
равномерно заряженным с линейной
плотностью заряда
![]() Определить работу сил поля по перемещению
точечного заряда
Определить работу сил поля по перемещению
точечного заряда![]() из точки, находящейся на расстоянии
из точки, находящейся на расстоянии![]() в точку находящуюся на расстоянии
в точку находящуюся на расстоянии![]() от поверхности цилиндра, в средней
его части.
от поверхности цилиндра, в средней
его части.
Решение:
Работа сил поля по перемещению заряда
равна
![]() Для нахождения разности потенциалов
воспользуемся соотношением
Для нахождения разности потенциалов
воспользуемся соотношением![]() Для поля с осевой симметрией, каким
является поле цилиндра, можно написать
Для поля с осевой симметрией, каким
является поле цилиндра, можно написать
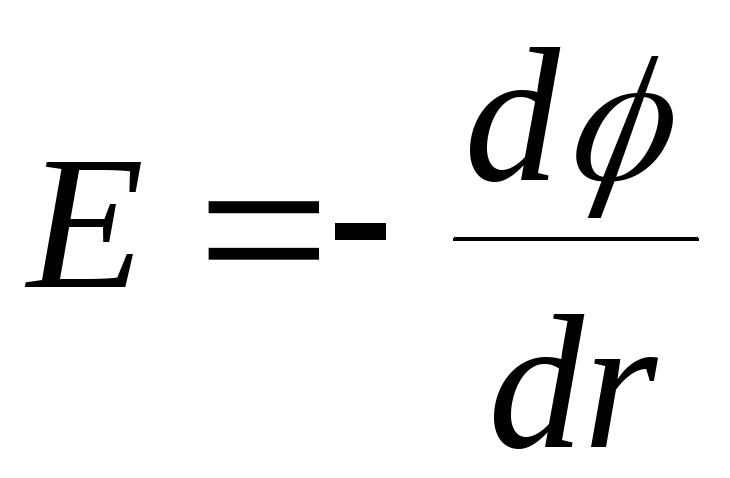 или
или
![]() .
.
Интегрируя это
выражение, найдём разность потенциалов
двух точек, отстоящих на расстояниях
![]() и
и![]() от оси цилиндра:
от оси цилиндра:
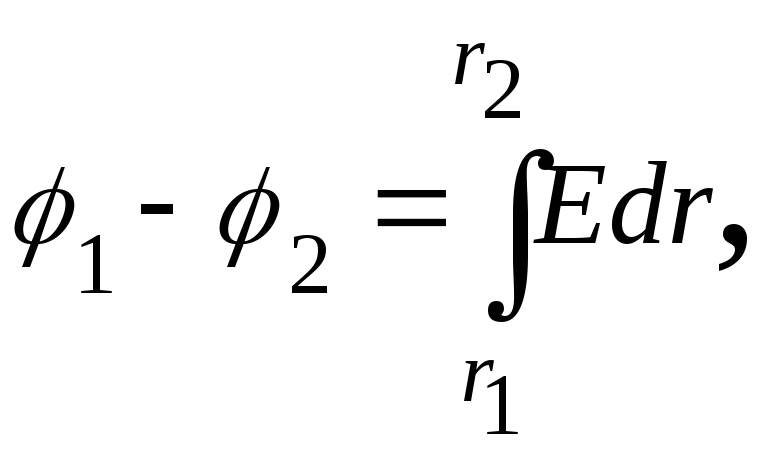 (1)
(1)
где
![]()
![]()
Так как цилиндр длинный и точки взяты вблизи его средней части, то можно воспользоваться формулой напряжённости поля, создаваемого бесконечно длинным цилиндром
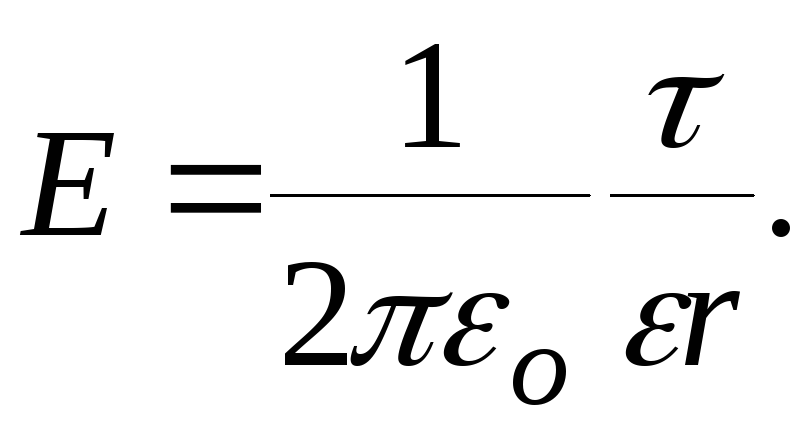 (2)
(2)
Подставив (2) в (1), получим
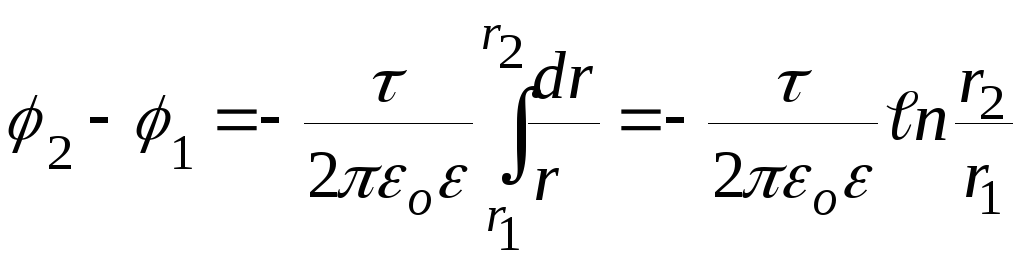 ,
,
или
 . (3)
. (3)
Таким образом
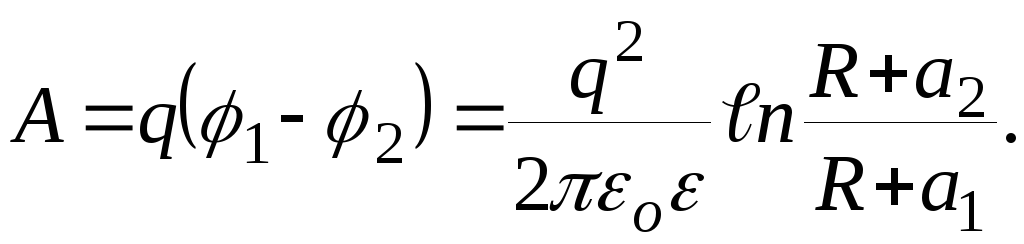
Проверим, даёт ли расчётная формула единицу работы. Для этого в правую часть вместо символов величин подставим их единицы:
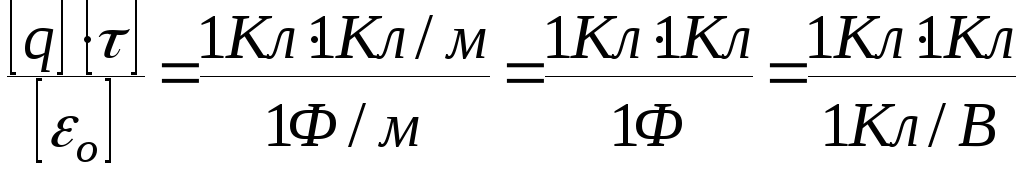 =
=
![]()
![]()
Выразим все величины
в единицах СИ:
![]() Кл/м,
Кл/м,![]() ,
,![]() ,
,![]() .
Учитывая, что величины
.
Учитывая, что величины![]() и
и![]() входят в формулу (3) в виде отношения, их
можно выразить в сантиметрах.
входят в формулу (3) в виде отношения, их
можно выразить в сантиметрах.
Произведём вычисления:
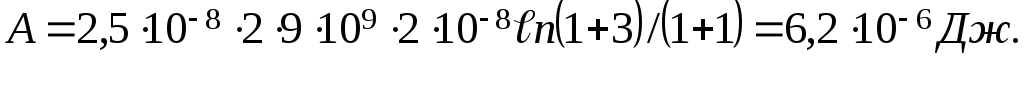 Пример
6. Электрическое
поле создано тонкой бесконечно длинной
нитью, равномерно заряженной с
линейной плотностью заряда
Пример
6. Электрическое
поле создано тонкой бесконечно длинной
нитью, равномерно заряженной с
линейной плотностью заряда
![]() На расстоянии а = 20 см от нити находится
плоская круглая площадка радиусомR
= 1 cм.
Определить поток вектора напряжённости
через площадку, если её плоскость
составляет угол
На расстоянии а = 20 см от нити находится
плоская круглая площадка радиусомR
= 1 cм.
Определить поток вектора напряжённости
через площадку, если её плоскость
составляет угол
![]() с линией напряжённости, проходящей
через середину площадки.
с линией напряжённости, проходящей
через середину площадки.
Решение: Поле, создаваемое нитью, является неоднородным, так как
 (1)
(1)
Поэтому поток
вектора
![]() равен
равен
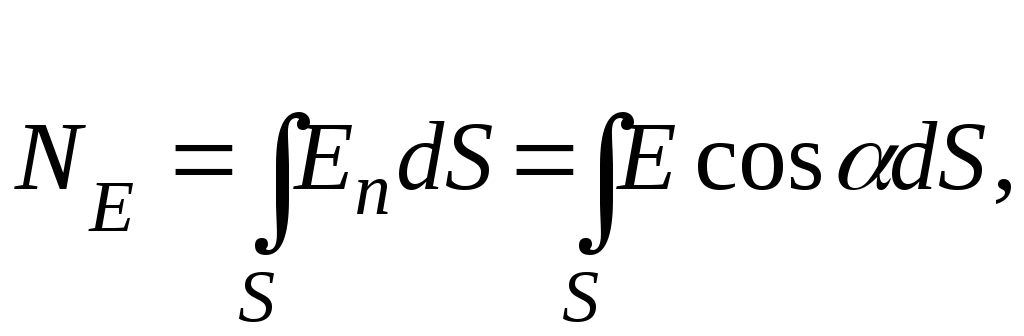
где
![]() - угол между векторами
- угол между векторами![]() и
и![]() (рис 5.).
(рис 5.).
Т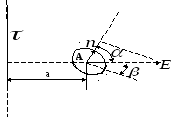 ак
как размеры площадки малы по сравнению
с расстоянием до нити
ак
как размеры площадки малы по сравнению
с расстоянием до нити![]() ,
то Е в пределах площадки меняется
незначительно. Поэтому значения Е и
,
то Е в пределах площадки меняется
незначительно. Поэтому значения Е и![]() под знаком интеграла можно заменить их
средними значениями
под знаком интеграла можно заменить их
средними значениями![]() и
и
![]() и вынести за знак
интеграла
и вынести за знак
интеграла
Рис 5.
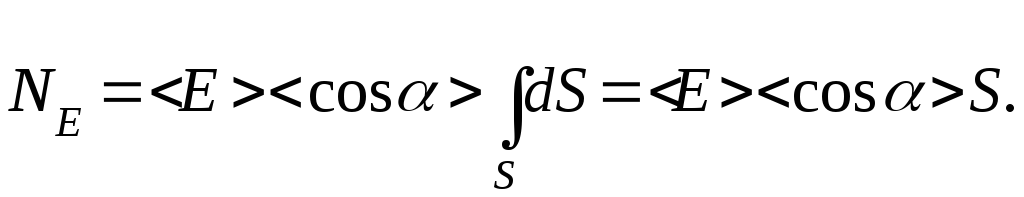
Заменяя
![]() и
и![]() их приближёнными значениями
их приближёнными значениями![]() и
и![]() ,
вычисленными для средней точки площадки,
получим
,
вычисленными для средней точки площадки,
получим
![]() .
(2)
.
(2)
Из рис. 5 следует,
что
![]() .
С учётом этого формула (2) примет вид
.
С учётом этого формула (2) примет вид
![]()
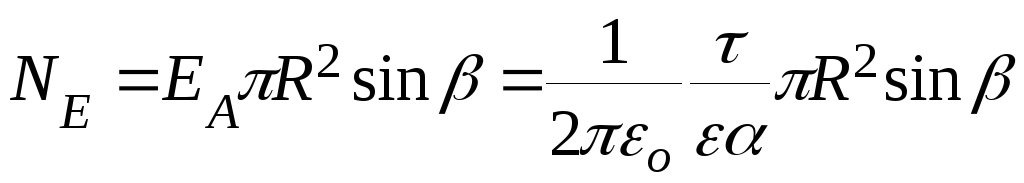 .
.
Выразим все величины
в единицах СИ:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Рисс. 5
Произведём вычисления:

Пример 7.
Электрон движется вдоль силовой линии
однородного электрического поля. В
некоторой точке поля с потенциалом
![]() электрон имел скорость
электрон имел скорость![]()
![]() определить потенциал
определить потенциал![]() точки поля, дойдя до которой электрон
потеряет половину своей скорости.
точки поля, дойдя до которой электрон
потеряет половину своей скорости.
Решение:
Из-за отсутствия сил трения полная
механическая энергия электрона не
изменяется, то есть
![]() где
где![]() кинетическая
и
кинетическая
и![]() - потенциальная энергия электрона. В
начале движения
- потенциальная энергия электрона. В
начале движения
 , (1)
, (1)
в конце движения
с учётом того, что
![]()
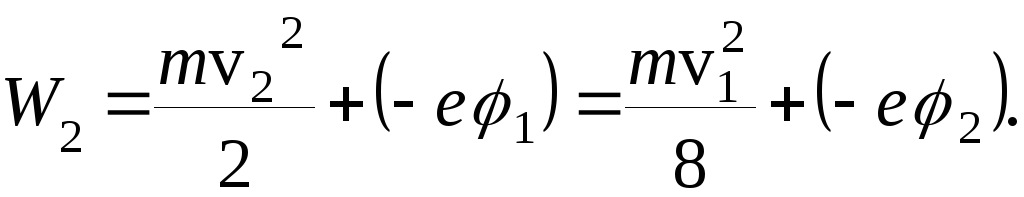 (2)
(2)
Приравнивая выражение (1) и (2), получим для потенциала

Выразим все величины
в единицах СИ:
![]() ,
,![]() ,
,![]()
Произведём вычисления:
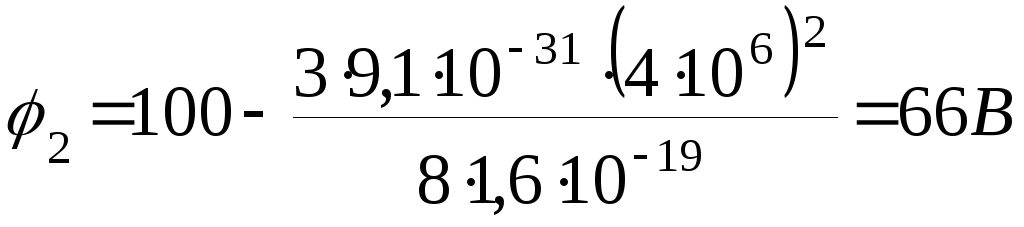
Возможен и другой подход к решению. Изменение кинетической энергии частицы равно работе результирующей силы, т.е.
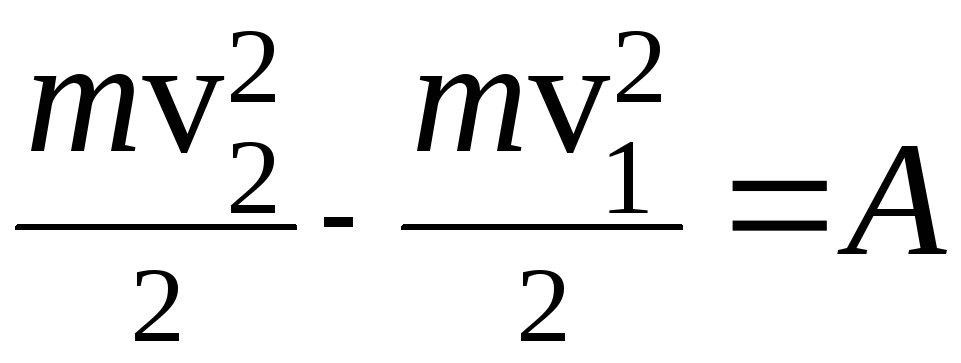 .
.
Так как электрон
тормозится силами поля, то
![]() .
.
Пример 8.
Сила взаимного притяжения пластин
плоского воздушного конденсатора
![]() Площадь каждой пластины
Площадь каждой пластины![]() Определить объёмную плотность энергии
поля конденсатора.
Определить объёмную плотность энергии
поля конденсатора.
Решение: Объёмная плотность энергии поля конденсатора
 , (1)
, (1)
где
![]() - напряжённость электрического поля
между пластинами конденсатора,
- напряжённость электрического поля
между пластинами конденсатора,
![]() - поверхностная
плотность заряда на пластинах.
- поверхностная
плотность заряда на пластинах.
Подставив выражение для Е в (1), получим
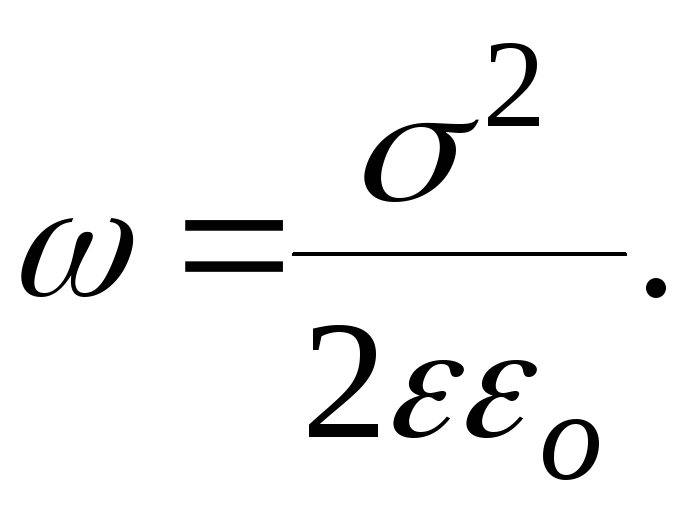 (2)
(2)
Найдём силу
взаимного притяжения пластин. Заряд
![]() одной пластины находится в поле
напряжённостью
одной пластины находится в поле
напряжённостью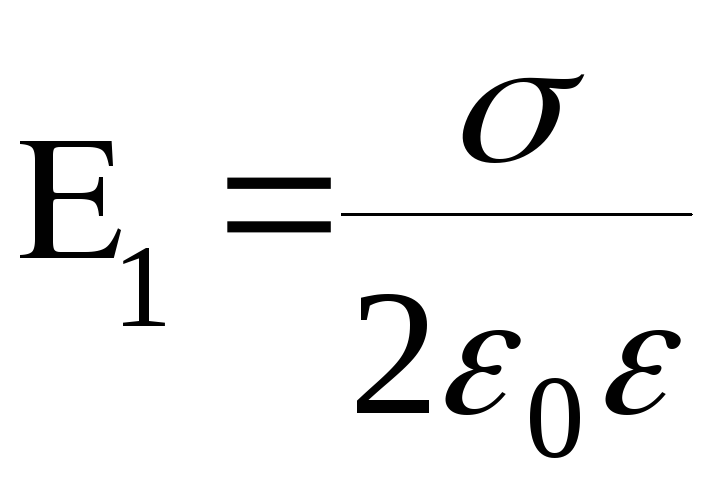 созданным зарядом другой пластины
конденсатора. Следовательно, на первый
заряд действует сила
созданным зарядом другой пластины
конденсатора. Следовательно, на первый
заряд действует сила
 (3)
(3)
Выразив
![]() из выражения (3) и подставив в (2), получим
из выражения (3) и подставив в (2), получим
![]() .
.
Проверим, даёт ли расчётная формула единицу объёмной плотности энергии. Для этого в правую часть формулы вместо величин подставим их единицы измерений:
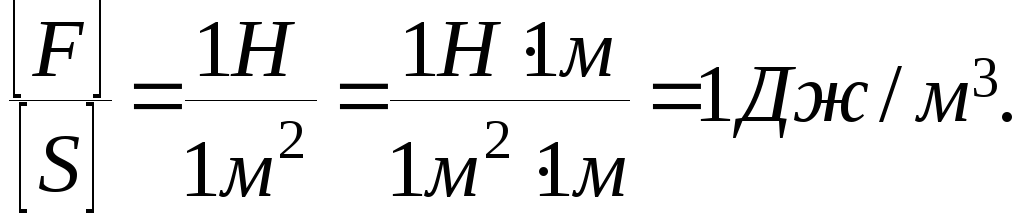
Выразим все величины
в единицах СИ:
![]()
![]() .
.
Произведём вычисления:

Пример 9.
Между пластинами плоского конденсатора,
заряженного до разности потенциалов
![]() находятся два слоя диэлектриков: стекла
толщиной
находятся два слоя диэлектриков: стекла
толщиной![]() и эбонита толщиной
и эбонита толщиной![]() Площадь каждой пластины
Площадь каждой пластины![]() Определить
Определить
а) напряжённость поля Е, индукцию D и падение потенциала U в каждом слое;
б) электрическую ёмкость конденсатора С.
Решение:
При переходе через границу раздела
диэлектриков нормальная составляющая
вектора
![]() в обоих слоях диэлектриков имеет
одинаковые значения
в обоих слоях диэлектриков имеет
одинаковые значения![]() .
.
В конденсаторе
силовые линии вектора
![]() перпендикулярны к границе раздела
диэлектриков, следовательно,
перпендикулярны к границе раздела
диэлектриков, следовательно,![]() и
и![]() .
Поэтому
.
Поэтому
![]() (1)
(1)
Учитывая, что![]() ,
и сокращая на
,
и сокращая на![]() из равенства (1)
из равенства (1)
получим
![]() , (2)
, (2)
где
![]() и
и![]() -
напряжённости поля в первом и во втором
слоях диэлектриков,
-
напряжённости поля в первом и во втором
слоях диэлектриков,![]() и
и![]() - диэлектрические проницаемости слоёв.
- диэлектрические проницаемости слоёв.
Разность потенциалов между пластинами конденсатора очевидно равна сумме напряжений на слоях диэлектриков
![]() (3)
(3)
В пределах каждого
слоя поле однородно, поэтому
![]() и
и![]() С учётом этого равенство (3) примет вид
С учётом этого равенство (3) примет вид
![]() (4)
(4)
Решая совместно уравнения (2) и (4), получим
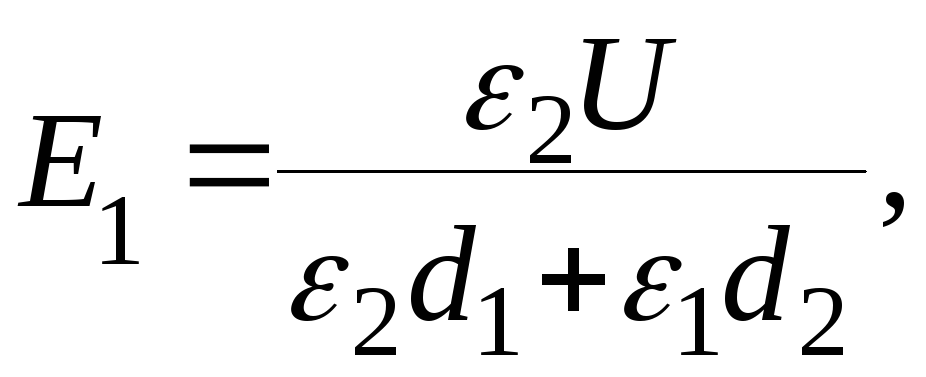

Выразим все
величины в единицах СИ:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
Произведём вычисления:
 ,
,
 ,
,
![]() ,
,
![]() ,
,
![]()
Определим ёмкость конденсатора
![]() (5)
(5)
где
![]() - заряд каждой пластины конденсатора.
- заряд каждой пластины конденсатора.
Учитывая, что
поверхностная плотность зарядов
![]() на пластинах конденсатора численно
равна модулю электрического смещения,
т.е.
на пластинах конденсатора численно
равна модулю электрического смещения,
т.е.![]() получим
получим
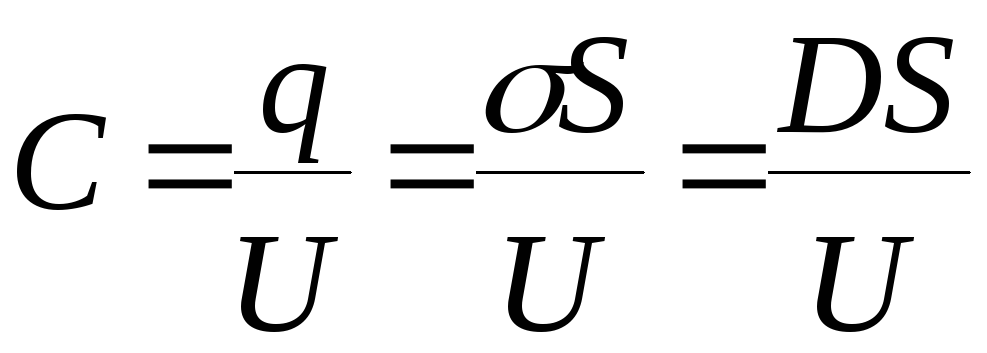 .
.
Проверим, даёт ли расчётная формула единицу электроёмкости. Для этого в правую часть формулы вместо символов величин подставим их единицы измерений:
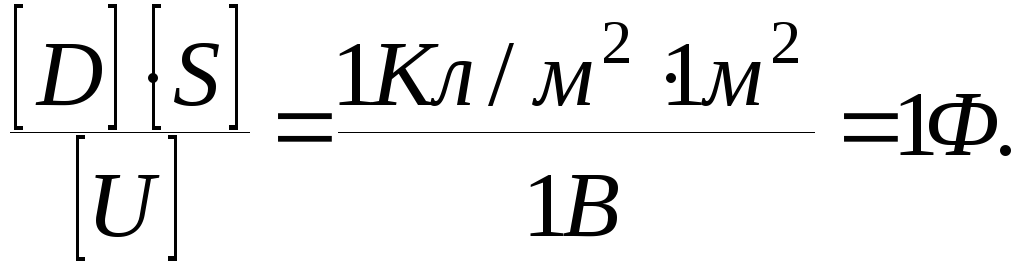
Произведём вычисления:
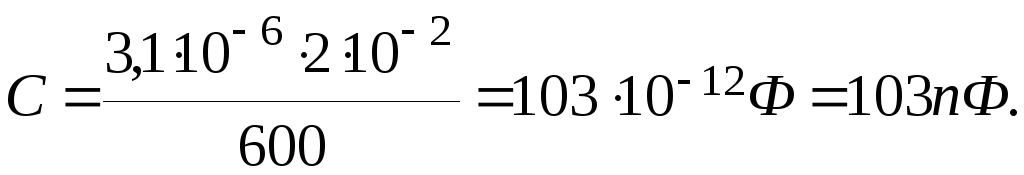
Пример 10.
Сила тока в проводнике сопротивлением
![]() Ом
равномерно нарастает от 0 до
Ом
равномерно нарастает от 0 до![]() в течение времени
в течение времени![]() Определить количество теплоты,
выделившейся в проводнике за первые
три секунды.
Определить количество теплоты,
выделившейся в проводнике за первые
три секунды.
Решение:
Закон Джоуля - Ленца в виде
![]() справедлив для постоянного тока. Так
как сила тока является функцией времени,
то
справедлив для постоянного тока. Так
как сила тока является функцией времени,
то![]() где
где![]() коэффициент
пропорциональности, характеризующий
скорость изменения силы тока ,
коэффициент
пропорциональности, характеризующий
скорость изменения силы тока ,

В этом случае закон Джоуля - Ленца справедлив для бесконечно малого интервала времени, т.е.
![]()
За первые три секунды выделится количество теплоты
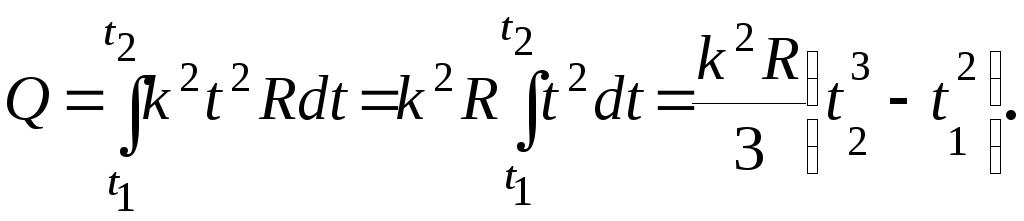
Произведём
вычисления:
![]()
