
- •Содержание
- •1. Основные понятия и определения
- •1.1. Структура персональной ЭВМ
- •1.2. Размещение данных и программ в памяти ПЭВМ
- •1.3. Программные модули
- •1.4. Ошибки
- •1.5. Функциональная и модульная декомпозиции
- •1.6. Файловая система хранения информации
- •1.7. Операционная система
- •2. Понятие алгоритмов и способы их описания
- •2.1. Свойства алгоритмов
- •2.2. Способы описания алгоритмов
- •3. Базовые элементы языка Cи
- •3.1. Алфавит языка
- •3.2. Лексемы
- •3.3. Идентификаторы и ключевые слова
- •3.4. Знаки операций
- •3.5. Литералы (константы)
- •3.6. Комментарии
- •4. Базовые типы объектов
- •4.1. Простейшая программа
- •4.2. Основные типы данных
- •4.3. Декларация объектов
- •4.4. Данные целого типа (int)
- •4.5. Данные символьного типа (char)
- •4.6. Данные вещественного типа (float, double)
- •5. Константы в программах
- •5.1. Целочисленные константы
- •5.2. Константы вещественного типа
- •5.3. Символьные константы
- •5.4. Строковые константы
- •6. Обзор операций
- •6.1. Операции, выражения
- •6.2. Арифметические операции
- •6.3. Операции присваивания
- •6.4. Сокращенная запись операции присваивания
- •6.5. Преобразование типов операндов арифметических операций
- •6.6. Операция приведения типа
- •6.7. Операции сравнения
- •6.8. Логические операции
- •6.9. Побитовые логические операции, операции над битами
- •6.10. Операция «,» (запятая)
- •7. Обзор базовых инструкций языка Си
- •7.1. Стандартная библиотека языка Си
- •7.2. Стандартные математические функции
- •7.3. Функции вывода данных
- •7.4. Функции ввода информации
- •7.5. Ввод - вывод потоками
- •8. Синтаксис операторов языка Cи
- •8.1. Условные операторы
- •8.2. Условная операция «? :»
- •8.3. Оператор выбора альтернатив (переключатель)
- •9. Составление циклических алгоритмов
- •9.1. Понятие цикла
- •9.2. Оператор с предусловием while
- •9.3. Оператор цикла с постусловием do – while
- •9.4. Оператор цикла с предусловием и коррекцией for
- •10. Операторы передачи управления
- •10.1. Оператор безусловного перехода goto
- •10.2. Оператор continue
- •10.3. Оператор break
- •10.4. Оператор return
- •11.1. Операции над указателями (косвенная адресация)
- •11.2. Ссылка
- •12. Массивы
- •12.1. Одномерные массивы
- •12.2. Многомерные массивы
- •12.3. Операция sizeof
- •12.4. Применение указателей
- •12.5. Указатели на указатели
- •13. Работа с динамической памятью
- •13.1. Пример создания одномерного динамического массива
- •13.2. Пример создания двухмерного динамического массива
- •14. Строки в языке Си
- •14.1. Русификация под Visual
- •15. Функции пользователя
- •15.1. Декларация функции
- •15.2. Вызов функции
- •15.3. Операция typedef
- •15.4. Указатели на функции
- •16. Классы памяти и области действия объектов
- •16.1. Автоматические переменные
- •16.2. Внешние переменные
- •16.3. Область действия переменных
- •17. Структуры, объединения, перечисления
- •17.1. Структуры
- •17.2. Декларация структурного типа данных
- •17.3. Создание структурных переменных
- •17.4. Вложенные структуры
- •17.5. Массивы структур
- •17.6. Размещение структурных переменных в памяти
- •17.7. Объединения
- •17.8. Перечисления
- •18. Файлы в языке Си
- •18.1. Открытие файла
- •18.2. Закрытие файла
- •18.3. Запись – чтение информации
- •18.4. Текстовые файлы
- •18.5. Бинарные файлы
- •Литература
- •Приложение 1. Таблицы символов ASCII
- •Приложение 2. Операции языка Си
- •Приложение 3. Возможности препроцессора
- •1. Вид рабочего стола консольного приложения Visual C++
- •2. Создание нового проекта
- •3. Добавление к проекту файлов с исходным кодом
- •4. Компиляция, компоновка и выполнение проекта
- •5. Конфигурация проекта
- •6. Открытие существующего проекта
- •Приложение 5. Некоторые возможности отладчика Visual C++
- •1. Установка точки прерывания
- •2. Пошаговое выполнение программы
- •3. Проверка значений переменных во время выполнения программы
- •4. Окна Auto и Watch 1
- •5. Программные средства отладки
- •ЧАСТЬ 2
- •1. Системы счисления
- •1.1. Общие определения
- •1.2. Алгоритмы перевода из одной системы счисления в другую
- •2. Организация памяти и структуры данных
- •3. Линейные списки и рекурсия
- •4. Динамическая структура данных – СТЕК
- •5. Динамическая структура данных – ОЧЕРЕДЬ
- •6. Двунаправленный линейный список
- •7. Построение обратной польской записи
- •8. Нелинейные структуры данных
- •Пояснение к программе
- •9. Понятие хеширования
- •9.1. Хеш-функция и хеш-таблица
- •9.2. Схемы хеширования
- •10. Элементы теории погрешностей
- •10.1. Методы реализации математических моделей
- •10.2. Источники погрешностей
- •10.3. Приближенные числа и оценка их погрешностей
- •10.4. Прямая задача теории погрешностей
- •10.5. Обратная задача теории погрешностей
- •10.6. Понятия устойчивости, корректности и сходимости
- •11. Вычисление интегралов
- •11.1. Формулы численного интегрирования
- •11.2. Формула средних
- •11.3. Формула трапеций
- •11.4. Формула Симпсона
- •11.5. Схема с автоматическим выбором шага по заданной точности
- •12. Методы решения нелинейных уравнений
- •12.1. Итерационные методы уточнения корней
- •12.2. Метод Ньютона
- •12.3. Метод секущих
- •12.4. Метод Вегстейна
- •12.5. Метод парабол
- •12.6. Метод деления отрезка пополам
- •13. Решение систем линейных алгебраических уравнений
- •13.1. Прямые методы решения СЛАУ
- •13.2. Метод Гаусса
- •13.3. Метод прогонки
- •13.4. Метод квадратного корня
- •13.5. Итерационные методы решения СЛАУ
- •13.6. Метод простой итерации
- •14. Поиск и сортировка
- •14.1. Последовательный поиск в массиве
- •14.2. Барьерный последовательный поиск
- •14.3. Сортировка вставками (включениями)
- •14.4. Двоичный поиск
- •14.5. Сортировка выбором
- •14.6. Алгоритмы сортировки выбором
- •14.7. Сортировка обменом
- •14.8. Быстрая сортировка
- •15. Обработка статистических данных
getch();
}
В результате получим:
Array: 7 11 19 37 41 53 61 79
15. Обработка статистических данных
Генеральная совокупность – множество статистических данных, количество которых достаточно велико. Получить необходимые сведения о генеральной совокупности, не обрабатывая всех ее данных можно, используя выборочный метод [5].
Предположим, что генеральная совокупность – случайная величина X, имеющая:
–плотность вероятности f(x);
–функцию распределения F(x);
–математическое ожидание M[X];
–дисперсию D[X].
Но ничего из приведенного выше мы не знаем, а знаем только значения элементов, составляющих эту генеральную совокупность.
Выборочный метод заключается в том, что из генеральной совокупности, объем которой стремится к бесконечности (в общем случае), производится случайный выбор некоторого небольшого количества данных, называемый выборка – {xi} ( i =1,...,N) . Объем выборки – значение N (количество данных в выборке).
Выборка должна быть «представительской», т.е. хорошо описывать поведение исследуемой случайной величины Х.
Далее строится вариационный ряд, т.е. данные выборки упорядочивают по возрастанию. Эти данные, называемые вариантами, могут быть сведены в таблицу, данные которой понадобятся в дальнейшем:
xi |
x1 |
x2 |
x3 |
. . . |
xn |
x > xn |
koli |
kol1 |
kol2 |
kol3 |
|
koln |
– |
p*i |
p*1 |
p*2 |
p*3 |
|
p*n |
– |
F*(x) |
0 |
p*1 |
p*1+ p*2 |
|
p*1+ . . . +p*n-1 |
1 |
Некоторые данные в выборке могут повторяться, поэтому n ≤ N.
Частоту повторения варианты xi в выборке обозначим koli – (чаще = 1), сум-
ма всех koli = N ( i =1,...,N) .
Частость (относительную частоту), т.е. отношение частоты к объему выборки можем принять за приближенное значение вероятности соответствующей ва-
рианты, т.е. p*i = koli/N (i =1,...,N) .
213

Причем, сумма всех p*i = 1 (i =1,...,N) .
Расчет эмпирической функции распределения F*(x)
При N→∞ эмпирическая функция распределения по вероятности сходится к теоретической функции распределения F(x). Эмпирическая функция распределения находится по формуле:
F*(x) = сумме p*i при X < xi , где p*i = koli/N,
т.е. равна количеству значений в вариационном ряду, строго меньших х, разделенному на N.
F*(x) = 0 при х ≤ x1 F*(x) = p*1 при х < x2 F*(x) = p*1+p*2 при х < x3
. . .
F*(x) = p*1+…+p*n-1 при х < xn-1 F*(x) = 1 при х > xn
Полученные данные можно добавить в таблицу.
Оценки числовых характеристик
1. Несмещенная состоятельная оценка математического ожидания, которая называется выборочное среднее, вычисляется по формуле (2.8) [5]:
x =1 ∑n xi .
n i=1
2. Несмещенная состоятельная оценка дисперсии при неизвестном математическом ожидании вычисляется по формуле (2.9) [5]:
|
1 |
n |
|
S02 = |
∑(xi −x)2 . |
||
|
|||
|
n −1 i=1 |
||
3. Смещенная состоятельная оценка дисперсии вычисляется по формуле
(2.10) [5]:
S 2 =1 ∑n (xi −x)2 . n i=1
4. Очевидно, что состоятельная оценка среднеквадратического отклонения:
S0 =  S02 .
S02 .
Гистограмма распределения
Гистограммой называется оценка плотности вероятности, т.е. приближенное значение f(x), поэтому ее будем обозначать f*(x). Наиболее часто используется равноинтервальная гистограмма.
Равноинтервальная гистограмма
При построении гистограммы отрезок [x1, xn] разбивают на m интервалов:
214
m= (int) N , для N ≤ 100.
N , для N ≤ 100.
Находят шаг h = (xn - x1)/m и для удобства строят таблицу
Интервалы |
[x*1, x*2] |
[x*2, x*3] |
. . . |
[x*m, x*m+1] |
kol*i |
kol*1 |
kol*2 |
|
kol*m |
f*i |
f*1 |
f*2 |
|
f*m |
Очевидно, что x*i = x1 + h*(i-1), а kol*i – количество элементов выборки, попавших в i-тый интервал.
При построении гистрограммы на каждом интервале строится прямоугольник с основанием h и высотой
f*i = kol*i / (N*h),
где f*i – средняя плотность вероятности.
Равновероятностная гистограмма
В равновероятностной гистограмме шаги рассчитываются из условия, чтобы в каждый интервал попало одинаковое число значений, равное m.
Для построения равновероятностной гистрограммы на каждом интервале строится прямоугольник с основанием hi и высотой f*i = m / (N*hi).
Например, значения 2, 3, 3, 3, 4; распределим 3 равномерно на интервале:
шаг = (4-2)/(кол-1);
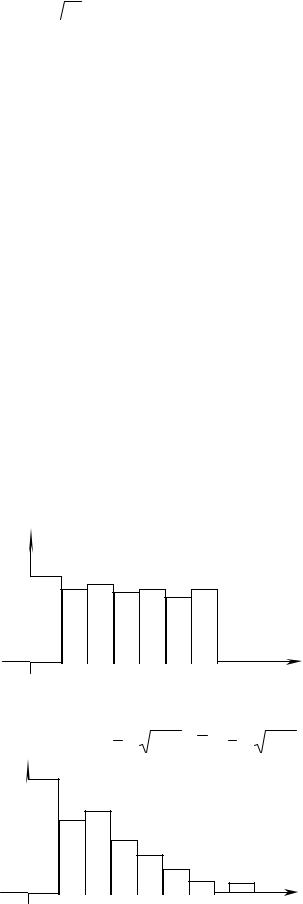
По виду гистограммы выдвигается гипотеза о законе распределения случайной величины Х.
Например
1). f*(x)
По данной гистограмме выдвигаем гипотезу о равномерном законе распре-
деления R( ˆ ˆ ), имеющем два параметра a и b, в данном случае – их оценки, вы- a,b
числяемые по формулам aˆ = x − |
3S 2 , b = x + |
3S 2 . |
|
2). |
f*(x) |
|
|
215
По данной гистограмме, если все xi > 0, выдвигаем гипотезу об экспоненциальном законе распределения E(1/ x ), имеющем один параметр λ, в данном случае
– его оценку, равную 1/ x .
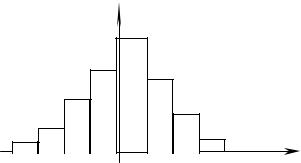
3). |
f*(x) |
По данной гистограмме выдвигаем гипотезу о нормальном законе распределения N( x , S0), имеющем два параметра а – математическое ожидание, σ – среднеквадратическое отклонение, в нашем случае – их оценки.
Критерий согласия "Xи-квадрат"
Проверяем выдвинутую гипотезу
H0 = f*(x) = f0(x);
H1 = f*(x) ≠ f0(x);
где f0(x) – плотность вероятности гипотетического (предполагаемого) закона распределения.
Вычисляем значение критерия по формуле (2.25) [5]:
|
k |
( p |
− p* )2 |
k |
(kol |
−N p |
)2 |
χ2 |
=N ∑ |
i |
i |
= ∑ |
i |
i |
|
|
pi |
|
N pi |
|
|||
|
i=1 |
|
i=1 |
|
|
где pi – теоретические вероятности, которые рассчитываются по следующим формулам [5]:
1)равномерный закон pi = (x*i+1 - x*i)/ (xn - x1) – формула (2.27);
2)экспоненциальный закон pi = exp(-x*i / x ) – exp(-x*i+1 / x ) x*i) – формула
(2.26); причем x*1 = 0, x*m+1 = +∞.
|
|
|
|
* |
−x |
|
|
* |
−x |
|
|
|
|
3) нормальный закон p |
=0,5 |
|
Φ |
xi+1 |
|
−Φ |
xi |
|
|
– формула (2.28); |
|||
|
|
|
|
||||||||||
i |
|
|
S |
|
|
|
S |
|
|
|
|||
|
|
|
|
0 |
|
|
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
причем x*1 = -∞, x*m+1 = +∞. Значения функции (интеграла) Лапласса Ф(х) можно рассчитать, используя методы приближенного интегрирования, или – по таб-
лицам. Напомним, что Ф(-х) = - Ф(х), а для х>4 Ф(х)=1(или 0,5, в зависимости от множителя перед интегралом – 1(2)/на корень из Pi*сигма).
Из таблицы функции «Хи-квадрат» для уровня значимости α=0,05 и k – число степеней свободы
k = m – 1 – s ,
где m – число интервалов, s – число параметров распределения, выбираем соответствующие значения:
216

X2 (0,05; 8) = 15,51;
X2 (0,05; 7) = 14,07.
Если расчетное (полученное нами) значение Х2 < X2 (0,05; k), то выдвинутая гипотеза H0 – принимается, хотя она может быть и не верна. В противном случае, гипотеза отвергается.
Критерий согласия Колмогорова
Проверяем выдвинутую гипотезу: H0 = F*(x) = F0(x);
H1 = F*(x) ≠ F0(x);
где F0(x) – теоретическая функция распределения, значения которой рассчитываются по следующим формулам [5]:
1) равномерный закон формула (2.30):
|
0; |
x < x1 ; |
F0(x) = |
(x - x1 ) / (xn - x1); |
x [ x1 , xn]; |
|
1; |
x ≥ xn . |
2) экспоненциальный закон формула (2.31): F0(x) = 1 - exp(-x / x ) ; x ≥ 0
3) нормальный закон формула (2.28):
|
|
x −x |
|
|
F0(x) = |
|
|
||
|
||||
0,5 + 0,5 Φ |
S0 |
. |
||
|
|
|
Рассчитывают 10-20 значений, по ним строят график теоретической функции там же, где построена эмпирическая функция.
Вычисляют значение критерия Колмогорова
λ = m*max|F*(x) – F0(x)| .
Из таблицы функции Колмогорова для уровня значимости α = 0,05, т.е. при
доверительной вероятности γ = 1-α = 0,95 выбирают значение критерия λγ =1,36. Если расчетное значение меньше табличного λ < λγ, выдвинутая гипотеза
H0 – ПРИНИМАЕТСЯ, хотя она может быть и НЕ ВЕРНА.
Выборка двухмерной случайной величины
Пусть задана выборка (x,y), объема n.
Несмещенная состоятельная оценка корреляционного момента вычисляется по формуле (2.13) [5]:
ˆ |
1 |
n |
Kxy = |
|
∑(xi −x) ( yi − y) , |
|
||
|
n −1 i=1 |
|
где x – выборочное среднее Х, y – выборочное среднее У.
217
Состоятельная оценка коэффициента корреляции (формула 2.14):
ˆ
rˆxy = 2 Kxy 2
 S0 (x) S0 ( y)
S0 (x) S0 ( y)
где S02 (x), S02 ( y) – несмещенные оценки дисперсий Х и У, соответственно. Простейшим видом регрессии является линейная:
y(x) =aˆ0 +aˆ1x ,
где оценки коэффициентов линейной регрессии вычисляем по формулам (2.35) и (2.36), соответственно:
|
|
ˆ |
|
|
|
|
|
aˆ |
= |
Kxy |
, |
aˆ |
0 |
= y −aˆ |
x . |
|
|||||||
1 |
|
S02 (x) |
|
|
1 |
|
|
|
|
|
|
|
|
|
218
Используемая литература
1.Котов В. и др. Методы алгоритмизации. Мн. Народная асвета. 1996.
2.Крячков А. и др. Программирование на С иС++. Практикум. М: Горячая
линия-Телеком. 2000.
3.Демидович Е.М. Основы алгоритмизации и программирования. Язык Си.
–Мн.: Бестпринт, 2001.
4.Синицын А.К., Навроцкий А.А. Алгоритмы вычислительной математики:
Лабораторный практикум по курсу «Программирование» для студентов 1-2-го курсов всех специальностей БГУИР. – Мн., БГУИР, 2002.
5.Аксенчик А.В., Волковец А.И. и др. Методические указания и контрольные задания по курсу «Теория вероятностей и математическая статистика» для студ. всех спец. БГУИР заочной формы обучения. – Мн.Ж БГУИР, 2002.
219
