
- •Содержание
- •1. Основные понятия и определения
- •1.1. Структура персональной ЭВМ
- •1.2. Размещение данных и программ в памяти ПЭВМ
- •1.3. Программные модули
- •1.4. Ошибки
- •1.5. Функциональная и модульная декомпозиции
- •1.6. Файловая система хранения информации
- •1.7. Операционная система
- •2. Понятие алгоритмов и способы их описания
- •2.1. Свойства алгоритмов
- •2.2. Способы описания алгоритмов
- •3. Базовые элементы языка Cи
- •3.1. Алфавит языка
- •3.2. Лексемы
- •3.3. Идентификаторы и ключевые слова
- •3.4. Знаки операций
- •3.5. Литералы (константы)
- •3.6. Комментарии
- •4. Базовые типы объектов
- •4.1. Простейшая программа
- •4.2. Основные типы данных
- •4.3. Декларация объектов
- •4.4. Данные целого типа (int)
- •4.5. Данные символьного типа (char)
- •4.6. Данные вещественного типа (float, double)
- •5. Константы в программах
- •5.1. Целочисленные константы
- •5.2. Константы вещественного типа
- •5.3. Символьные константы
- •5.4. Строковые константы
- •6. Обзор операций
- •6.1. Операции, выражения
- •6.2. Арифметические операции
- •6.3. Операции присваивания
- •6.4. Сокращенная запись операции присваивания
- •6.5. Преобразование типов операндов арифметических операций
- •6.6. Операция приведения типа
- •6.7. Операции сравнения
- •6.8. Логические операции
- •6.9. Побитовые логические операции, операции над битами
- •6.10. Операция «,» (запятая)
- •7. Обзор базовых инструкций языка Си
- •7.1. Стандартная библиотека языка Си
- •7.2. Стандартные математические функции
- •7.3. Функции вывода данных
- •7.4. Функции ввода информации
- •7.5. Ввод - вывод потоками
- •8. Синтаксис операторов языка Cи
- •8.1. Условные операторы
- •8.2. Условная операция «? :»
- •8.3. Оператор выбора альтернатив (переключатель)
- •9. Составление циклических алгоритмов
- •9.1. Понятие цикла
- •9.2. Оператор с предусловием while
- •9.3. Оператор цикла с постусловием do – while
- •9.4. Оператор цикла с предусловием и коррекцией for
- •10. Операторы передачи управления
- •10.1. Оператор безусловного перехода goto
- •10.2. Оператор continue
- •10.3. Оператор break
- •10.4. Оператор return
- •11.1. Операции над указателями (косвенная адресация)
- •11.2. Ссылка
- •12. Массивы
- •12.1. Одномерные массивы
- •12.2. Многомерные массивы
- •12.3. Операция sizeof
- •12.4. Применение указателей
- •12.5. Указатели на указатели
- •13. Работа с динамической памятью
- •13.1. Пример создания одномерного динамического массива
- •13.2. Пример создания двухмерного динамического массива
- •14. Строки в языке Си
- •14.1. Русификация под Visual
- •15. Функции пользователя
- •15.1. Декларация функции
- •15.2. Вызов функции
- •15.3. Операция typedef
- •15.4. Указатели на функции
- •16. Классы памяти и области действия объектов
- •16.1. Автоматические переменные
- •16.2. Внешние переменные
- •16.3. Область действия переменных
- •17. Структуры, объединения, перечисления
- •17.1. Структуры
- •17.2. Декларация структурного типа данных
- •17.3. Создание структурных переменных
- •17.4. Вложенные структуры
- •17.5. Массивы структур
- •17.6. Размещение структурных переменных в памяти
- •17.7. Объединения
- •17.8. Перечисления
- •18. Файлы в языке Си
- •18.1. Открытие файла
- •18.2. Закрытие файла
- •18.3. Запись – чтение информации
- •18.4. Текстовые файлы
- •18.5. Бинарные файлы
- •Литература
- •Приложение 1. Таблицы символов ASCII
- •Приложение 2. Операции языка Си
- •Приложение 3. Возможности препроцессора
- •1. Вид рабочего стола консольного приложения Visual C++
- •2. Создание нового проекта
- •3. Добавление к проекту файлов с исходным кодом
- •4. Компиляция, компоновка и выполнение проекта
- •5. Конфигурация проекта
- •6. Открытие существующего проекта
- •Приложение 5. Некоторые возможности отладчика Visual C++
- •1. Установка точки прерывания
- •2. Пошаговое выполнение программы
- •3. Проверка значений переменных во время выполнения программы
- •4. Окна Auto и Watch 1
- •5. Программные средства отладки
- •ЧАСТЬ 2
- •1. Системы счисления
- •1.1. Общие определения
- •1.2. Алгоритмы перевода из одной системы счисления в другую
- •2. Организация памяти и структуры данных
- •3. Линейные списки и рекурсия
- •4. Динамическая структура данных – СТЕК
- •5. Динамическая структура данных – ОЧЕРЕДЬ
- •6. Двунаправленный линейный список
- •7. Построение обратной польской записи
- •8. Нелинейные структуры данных
- •Пояснение к программе
- •9. Понятие хеширования
- •9.1. Хеш-функция и хеш-таблица
- •9.2. Схемы хеширования
- •10. Элементы теории погрешностей
- •10.1. Методы реализации математических моделей
- •10.2. Источники погрешностей
- •10.3. Приближенные числа и оценка их погрешностей
- •10.4. Прямая задача теории погрешностей
- •10.5. Обратная задача теории погрешностей
- •10.6. Понятия устойчивости, корректности и сходимости
- •11. Вычисление интегралов
- •11.1. Формулы численного интегрирования
- •11.2. Формула средних
- •11.3. Формула трапеций
- •11.4. Формула Симпсона
- •11.5. Схема с автоматическим выбором шага по заданной точности
- •12. Методы решения нелинейных уравнений
- •12.1. Итерационные методы уточнения корней
- •12.2. Метод Ньютона
- •12.3. Метод секущих
- •12.4. Метод Вегстейна
- •12.5. Метод парабол
- •12.6. Метод деления отрезка пополам
- •13. Решение систем линейных алгебраических уравнений
- •13.1. Прямые методы решения СЛАУ
- •13.2. Метод Гаусса
- •13.3. Метод прогонки
- •13.4. Метод квадратного корня
- •13.5. Итерационные методы решения СЛАУ
- •13.6. Метод простой итерации
- •14. Поиск и сортировка
- •14.1. Последовательный поиск в массиве
- •14.2. Барьерный последовательный поиск
- •14.3. Сортировка вставками (включениями)
- •14.4. Двоичный поиск
- •14.5. Сортировка выбором
- •14.6. Алгоритмы сортировки выбором
- •14.7. Сортировка обменом
- •14.8. Быстрая сортировка
- •15. Обработка статистических данных
12. Методы решения нелинейных уравнений
Математической моделью многих физических процессов является функциональная зависимость y=f(x). Поэтому задачи исследования различных свойств функции f(x) часто возникают в инженерных расчетах. Одной из таких задач является нахождение значений x, при которых функция f(x) обращается в ноль, т.е. решение уравнения
f(x)=0. |
(12.1) |
Точное решение удается получить в исключительных случаях, и обычно для нахождения корней уравнения применяются численные методы. Решение уравнения (12.1) при этом осуществляется в два этапа:
|
|
|
|
|
|
|
|
|
1. Приближенное опре- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
деление местоположения, ха- |
|
|
|
|
|
|
|
|
|
рактер и выбор интересую- |
|
|
|
|
|
|
|
|
|
щего нас корня. |
|
|
|
|
|
|
|
|
|
2. Вычисление выбран- |
|
|
|
|||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
ного корня с заданной точно- |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стью ε. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
Первая задача решается |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
Рис. 4 |
|
|
|
|
|
|
графическим методом: на за- |
|
|
|
|
|
|
|
|
|
данном отрезке [a,b] вычис- |
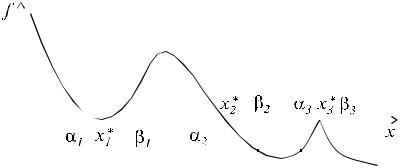
ляется таблица значений функции с некоторым шагом h, строится ее график и определяются интервалы (αi,βi) длиной h, на которых находятся корни. На рис.4 представлены три наиболее часто встречающиеся ситуации:
а) кратный корень: |
f |
′ |
* |
|
f (α1) f (β1) > 0; |
(x1 ) = 0, |
|
||||
б) простой корень: |
f |
′ |
* |
|
f (α2 ) f (β2 ) < 0; |
(x2 ) ≠ 0, |
* |
||||
|
|
|
′ |
не существует, f (α3) f (β3) > 0 . |
|
в) вырожденный корень: f (x3 ) |
|||||
Как видно из рис. 4, в случаях a) и в) значение корня совпадает с точкой экстремума функции и для нахождения таких корней рекомендуется использовать методы поиска минимума функции.
На втором этапе вычисление значения корня с заданной точностью осуществляется одним из итерационных методов. При этом, в соответствии с общей методологией m-шагового итерационного метода, на интервале (α,β), где находится интересующий нас корень x*, выбирается m начальных значений x0, x1, …, xm-1 (обычно x0=α, x1=β), после чего последовательно находятся члены (xm, xm+1, ..., xn-
1, |
xn) |
рекуррентной |
последовательности |
порядка m по правилу |
||||||
x |
=ϕ(x |
, ..., x |
) |
до тех пор, пока |
|
xn − xn−1 |
|
<ε |
. Последнее xn выбирается в ка- |
|
|
|
|||||||||
k |
k−1 |
k−m |
|
|
|
|
|
|||
честве приближенного значения корня (x*≈ xn).
Многообразие методов определяется возможностью большого выбора законов ϕ. Наиболее часто используемые на практике методы описаны ниже.
171
12.1. Итерационные методы уточнения корней |
|
|
|
|
||||
Очень часто в практике вычислений встречается ситуация, когда уравнение |
||||||||
(12.1) записано в виде разрешенном, относительно x: |
|
|
|
|
|
|||
x = ϕ(x). |
|
|
|
|
|
|
(12.2) |
|
Переход от записи уравнения (12.1) к эквивалентной записи (12.2) можно |
||||||||
сделать многими способами, например, положив |
|
|
|
|
|
|
||
ϕ(x) = x+ψ(x) f(x) , |
|
|
|
|
|
(12.3) |
||
где ψ(x) – произвольная, непрерывная, знакопостоянная функция (часто доста- |
||||||||
точно выбрать ψ=const). |
|
|
|
|
|
|
|
|
В этом случае корни уравнения (12.2) являются также корнями (12.1), и на- |
||||||||
оборот. |
|
|
|
|
|
|
|
|
12.2. Метод Ньютона |
|
|
|
|
|
|
|
|
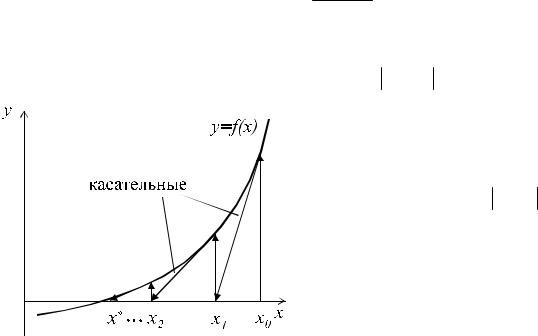
Этот метод часто называется методом касательных. Если f(x) имеет непре- |
||||||||
рывную производную, тогда, выбрав в (3) ψ(x) = 1/f’(x), получаем эквивалентное |
||||||||
уравнение x=x-f(x)/f’(x)=ϕ(x). Скорость сходимости рекуррентной последователь- |
||||||||
ности метода Ньютона |
|
|
|
|
|
|
|
|
x = x |
− f (xk−1) =ϕ(x |
k−1 |
) |
|
|
|
|
|
k |
k−1 |
f ′(xk−1) |
|
|
|
|
(12.4) |
|
|
|
|
|
|
|
|
||
вблизи корня очень большая, погрешность очередного приближения примерно |
||||||||
|
|
′′ |
|
2 |
|
|
|
|
равна квадрату погрешности предыдущего εk ϕ (x*) εk−1 . |
|
|
|
|
||||
|
|
Из (12.4) видно, что этот метод одно- |
||||||
|
|
шаговый (m=1) и для начала вычислений |
||||||
|
|
требуется задать одно начальное прибли- |
||||||
|
|
жение x0 из области сходимости, |
опреде- |
|||||
|
|
ляемой неравенством |
f f |
′′ |
′ 2 |
<1. Ме- |
||
|
|
|
/( f ) |
|||||
|
|
тод Ньютона получил название метод каса- |
||||||
|
|
тельных благодаря геометрической иллю- |
||||||
|
|
страции его сходимости, представленной на |
||||||
|
|
рис. 5. Этот метод позволяет находить как |
||||||
|
|
простые, так и кратные корни. Основной |
||||||
Рис. 5 |
|
его недостаток – малая область сходимости |
||||||
|
и необходимость вычисления производной |
|||||||
|
|
|||||||
f'(x).
12.3. Метод секущих
Данный метод является модификацией метода Ньютона, позволяющей избавиться от явного вычисления производной путем ее замены приближенной
172
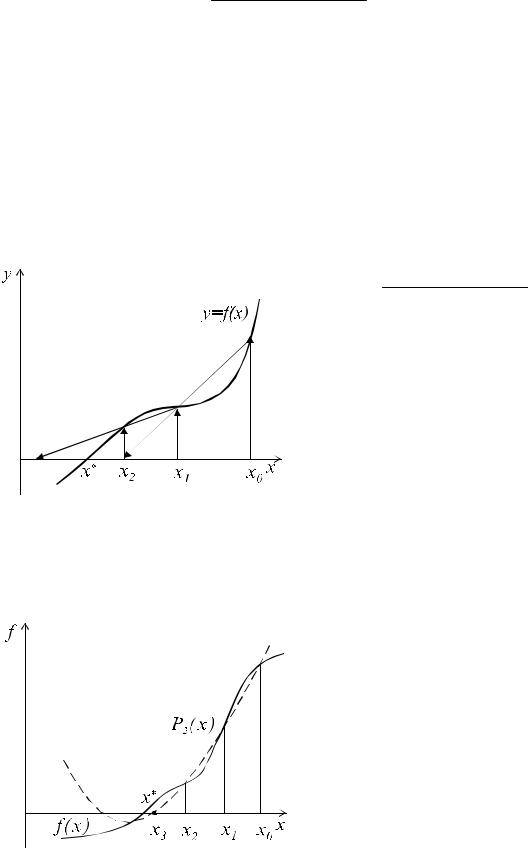
формулой. Это эквивалентно тому, что вместо касательной проводится секущая |
|||||||
(рис. 6). Тогда вместо процесса (12.4) получаем |
|
|
|||||
xk = xk−1 − |
|
f (xk−1)h |
|
=ϕ(xk−1) |
|
||
f (xk−1) − f (xk−1 |
− h) |
(12.5) |
|||||
|
|
. |
|||||
Здесь h – некоторый малый параметр метода, который подбирается из усло- |
|||||||
вия наиболее точного вычисления производной. |
|
|
|||||
Метод одношаговый (m=1), и его условие сходимости при правильном вы- |
|||||||
боре h такое же, как у метода Ньютона. |
|
|
|
|
|||
12.4. Метод Вегстейна |
|
|
|
|
|
||
Этот метод является модификацией метода секущих. В нем предлагается |
|||||||
при расчете приближенного значения производной по разностной формуле ис- |
|||||||
пользовать вместо точки xk-1-h |
в (12.5) точку xk-2, полученную на предыдущей |
||||||
итерации. Расчетная формула метода Вегстейна: |
|
|
|||||
|
|
x = x |
− f (xk−1)(xk−1 − xk−2 ) = |
|
|||
|
|
k |
k−1 |
f (xk−1) − f (xk−2 ) |
|
||
|
|
|
|
|
|||
|
|
=ϕ(xk−1, xk−2 ) |
. |
(12.6) |
|||
|
|
|
Метод является двухшаговым (m=2), |
||||
|
|
и для начала вычислений требуется задать 2 |
|||||
|
|
начальных приближения x0,x1. Лучше всего |
|||||
|
|
x0=α, x1=β. |
Метод Вегстейна |
сходится |
|||
|
|
медленнее метода секущих, однако, требует |
|||||
Рис. 6 |
|
в 2 раза меньшего числа вычислений f(x) и |
|||||
|
за счет этого оказывается более эффектив- |
||||||
ным. |
|
||||||
|
|
|
|
|
|
||
Схема алгоритма метода Вегстейна представлена на рис. 5.6 [4]. |
|
||||||
12.5. Метод парабол |
|
|
|
Предыдущие методы основаны на |
|
|
том, что исходная функция f(x) аппрокси- |
|
|
мируется линейной зависимостью вблизи |
|
|
корня и в качестве следующего приближе- |
|
|
ния выбирается точка пересечения аппрок- |
|
|
симирующей прямой с осью абсцисс. Ясно, |
|
|
что аппроксимация будет лучше, если вме- |
|
|
сто линейной зависимости использовать |
|
|
квадратичную. На этом и основан один из |
|
|
самых эффективных методов – метод пара- |
|
Рис. 7 |
бол. Суть его в следующем: задаются три |
|
начальные точки x0,x1,x2 (обычно x0=α, |
||
|
||
|
173 |

x2=β, x1=(α+β)/2), в этих точках рассчитываются три значения функции y=f(x), y0,y1,y2 и строится интерполяционный многочлен второго порядка (рис.7), который удобно записать в форме
|
|
P = a(x − x )2 +b(x − x ) + c = az2 |
+bz + c |
. |
|
|
(12.7) |
|||||||||||||||
|
|
|
2 |
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
Коэффициенты этого многочлена вычисляются по формулам: |
|
|||||||||||||||||||||
z=x-x2; z0=x0-x2; z1=x1-x2; c=y2; |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
a = |
( y |
0 |
− y |
2 |
)z |
−( y |
− y |
2 |
)z |
0 ; |
b = |
( y |
− y |
2 |
)z2 |
−( y |
|
− y |
2 |
)z2 |
|
|
|
|
1 |
|
1 |
|
|
0 |
|
1 |
1 |
|
0 |
|
|||||||||
|
|
|
z0 z1(z0 − z1) |
|
|
|
|
|
z0 z1(z1 − z0 ) |
|
. |
(12.8) |
||||||||||
Полином (12.7) имеет два корня: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
z |
|
= |
−b ± |
|
b2 |
− 4ac |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1, 2 |
|
|
|
2a |
|
, |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
из которых выбирается наименьший по модулю zm и рассчитывается следующая точка x3=x2+zm, в результате получается рекуррентная формула метода парабол:
xk = xk−1 + zm (xk−1, xk−2 , xk−3 ) =ϕ(xk−1, xk−2 , xk−3). |
(12.9) |
Метод трехшаговый (m=3). Скорость сходимости его больше, чем у метода Вегстейна, однако, не лучше, чем у метода Ньютона вблизи корня. Схема алгоритма метода парабол представлена на рис. 5.8 [4].
12.6. Метод деления отрезка пополам
Все вышеописанные методы могут работать, если функция f(x) является непрерывной и дифференцируемой вблизи искомого корня. В противном случае они не гарантируют получение решения.
Для разрывных функций, а также, если не требуется быстрая сходимость, для нахождения простого корня на интервале [α,β] применяют надежный метод деления отрезка пополам. Его алгоритм основан на построении рекуррентной последовательности по следующему закону: в качестве начального приближения выбираются границы интервала, на котором точно имеется один простой корень x0=α, x1=β, далее находится его середина x2=(x0+x1)/2; очередная точка x3 выбирается как середина того из смежных с x2 интервалов [x0,x2] или [x2,x1], на котором находится корень. В результате получается следующий алгоритм метода деления отрезка пополам:
1)вычисляем y0=f(x0) ;
2)вычисляем x2=(x0+x1)/2, y2=f(x2);
3)если y0 y2>0, тогда x0=x2, y0=y2,
иначе x1=x2;
4)если x1-x0>ε, тогда повторять с п.2;
5)вычисляем x*=(x0+x1)/2;
6)конец.
174
За одно вычисление функции погрешность уменьшается вдвое, то есть скорость сходимости невелика, однако метод устойчив к ошибкам округления и всегда сходится.
Рассмотрим функцию определения корня уравнения f(x)=0 на отрезке [а,b] с заданной точностью eps. Предположим для простоты, что исходные данные задаются без ошибок, т.е. eps>0, f(a)*f(b)<0, b>а, и вопрос о возможности существования нескольких корней на отрезке [а,b] нас не интересует. Не очень эффективная рекурсивная функция для решения поставленной задачи приведена в следую-
щей программе: |
|
|
|
. . . |
|
|
int counter = 0; |
// Счетчик обращений к тестовой функции |
// |
------- Нахождение корня уравнения методом деления отрезка пополам ---------- |
|
|
double Root(double f(double), double a, double b, double eps) |
|
|
{ |
|
double fa = f(a), fb = f(b), c, fc; if ( fa * fb > 0)
{
printf("\n На интервале a,b НЕТ корня!"); exit(1);
|
} |
|
|
c = (a + b) / 2.0; |
|
|
fc = f(c); |
|
|
if (fc == 0.0 || |
(b – a) < eps) return c; |
|
return (fa * fc < 0.0) ? Root(f, a, c, eps) : Root(f, c, b, eps); |
|
// |
} |
|
------------------------------------------------------void main() |
|
|
|
|
|
|
{ |
|
|
double x, a=0.1, b=3.5, eps=0.00001; |
|
|
double fun(double); |
// Прототип тестовой функции |
|
x = Root (fun, a, b, eps); |
|
|
printf ("\n Число обращений к тестовой функции = %d ", counter); |
|
|
printf ("\n Корень = %f ", x); |
|
|
getch(); |
|
|
} |
|
//----------------- |
Определение тестовой функции fun ------------------------------------ |
|
|
double fun (double x) |
|
|
{ |
|
|
counter++; |
// Счетчик обращений – глобальная переменная |
return (2.0/x * cos(x/2.0));
}
Значения A, B и EPS заданы постоянными только для тестового анализа полученных результатов, хотя лучше данные вводить с клавиатуры.
175
В результате выполнения программы с определенными в ней конкретными данными получим:
Число обращений к тестовой функции = 60
Корень = 3.141591
На рис. 5.9 [4] приведена схема определения всех корней функции f(x) в указанном интервале [a, b] – на экран выдается таблица значений функции и делается запрос на ввод начального приближения (это может быть α, β или x0) к тому корню, который надо получить с заданной точностью. После того как введены требуемые данные, идет обращение к подпрограмме и печать результатов.
176
