( t -> Prev ) -> Next = t1; t1 -> Prev = t -> Prev;
}
t -> Prev = t1;
puts("\n Insert! "); // Выводим сообщение return;
}
t = t -> Next;
} |
|
|
t1 |
-> Next = NULL; |
// В конец списка |
t1 |
-> Prev = end; |
|
end -> Next = t1; |
|
|
end = t1; |
|
|
puts("\n Insert End! "); |
// Сообщение - вставили в конец |
|
return;
}
7. Построение обратной польской записи
Одной из главных причин, лежащих в основе появления языков программирования высокого уровня, явились вычислительные задачи, требующие больших объемов вычислений. Поэтому к разработчикам языков программирования были предъявлены жесткие требования: максимальное приближение формы записи в коде программы математических выражений к естественному языку математики. Поэтому одной из первых областей системного программирования составили исследования способов трансляции математических выражений. И здесь были получены многочисленные результаты данных исследований, но наибольшее распространение получил метод трансляции при помощи обратной польской записи, которую предложил польский математик Я.Лукашевич. Ниже приводятся преимущества такого промежуточного постфиксного представления математического выражения. Но прежде давайте рассмотрим два основных алгоритма получения обратной польской записи.
Алгоритм 1. Данный алгоритм основан на представлении математического выражения в виде дерева и использовании третьего способа его обхода, который подробно рассмотрен в [1].
Напомним его на конкретном примере.
Пусть задано простое арифметическое выражение вида:
(A+B)*(C+D)–E . |
(1) |
Представим это выражение в виде дерева, в котором узлам соответствуют операции, а листьям – операнды. Построение начинается с корня, в качестве которого выбирается операция, которая выполнятся последней. Левой ветви соответ-
135
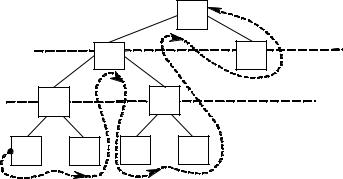
ствует левый операнд операции, а правой ветви – правый. Дерево выражения (1) имеет вид:
-
* |
E |
+ |
+ |
A |
B |
C |
D |
Совершим обход дерева, под которым понимается формирование строки из символов узлов и ветвей дерева. Обход будем совершать от самой левой ветви вправо и узел переписывать в выходную строку только после рассмотрения всех его ветвей. Обход совершаем строго по уровням.
Уровень 1: имеем АВ+CD+ Поднялись на Уровень 2: имеем *Е И наконец Корень.
Результат обхода дерева таким образом имеет вид:
AB+CD+*E– |
(2) |
Характерные особенности выражения (2) состоят в следовании символов операций за символами операндов и в отсутствии скобок. Такая запись и называется обратной польской записью.
Алгоритм 2. Использование стека. Получение обратной польской записи из исходного выражения может осуществляться весьма просто на основе простого алгоритма, предложенного Дейкстрой. Для этого он ввел понятие стекового приоритета операций, который приведен в таблице:
Операция |
Приоритет |
|
( |
|
0 |
) |
|
1 |
+ |
– |
2 |
* |
/ |
3 |
Суть алгоритма в следующем. Просматривается исходная строка символов слева направо, операнды переписываются в выходную строку, а знаки операций заносятся в стек на основе следующих соображений:
а) если стек пуст, то операция из исходной строки переписывается в стек; б) операция выталкивает из стека все операции с большим или равным при-
оритетом в выходную строку;
136
в) если очередной символ из исходной строки есть открывающая скобка, то он проталкивается в стек;
г) закрывающая круглая скобка выталкивает все операции из стека до ближайшей открывающей скобки, сами скобки в выходную строку не переписываются, а уничтожают друг друга.
Процесс получения обратной польской записи выражения (1) представлен в таблице:
Просматриваемый |
Входная |
Состояние стека |
Выходная |
||
символ |
строка |
|
|
|
строка |
1 |
( |
( |
|
|
|
2 |
A |
( |
|
|
A |
3 |
+ |
+ |
( |
|
|
4 |
B |
+ |
( |
|
B |
5 |
) |
|
|
|
+ |
6 |
|
|
|
|
|
7 |
( |
( |
|
|
|
8 |
C |
( |
|
|
C |
9 |
+ |
+ |
( |
|
|
10 |
D |
+ |
( |
|
D |
11 |
) |
|
|
|
+ |
12 |
– |
– |
|
|
|
13 |
E |
– |
|
|
E |
14 |
|
|
|
|
– |
Получим: AB+CD+*E–
Обратная польская запись обладает рядом замечательных свойств, которые превращают ее в идеальный промежуточный язык при трансляции.
Во-первых, вычисление выражения, записанного в обратной польской записи, может проводиться путем однократного просмотра, что является весьма удобным при генерации объектного кода программ.
Например, вычисление полученного выражения может быть проведено следующим образом:
Шаг |
Анализируемая строка |
Действие |
1 |
AB+CD+*E– |
R1=A+B |
2 |
R1CD+*E– |
R2=C+D |
3 |
R1R2*E– |
R1=R1*R2 |
4 |
R1E– |
R1=R1–E |
5 |
R1 |
|
Здесь R1 и R2 – вспомогательные переменные.
137
А теперь несколько примеров на использование только что рассмотренных алгоритмов.
Пример 1. Пусть опять задано математическое выражение a+b*c+(d*e+f)*g. Необходимо записать это выражение в постфиксной форме. Правильным ответом будет выражение abc*+de*f+g*+. Решаем эту задачу, используя стек.
Пусть исходная информация хранится в строке S=”a+b*c+(d*e+f)*g”. Результат будем получать в строке В.
Алгоритм решения
В начале стек пуст, В – пустая строка, S = ”a+b*c+(d*e+f)*g”.
Первым читается символ «a», т.к. он не является операцией, то помещается в строку В. Затем читаем «+» и помещаем в стек. Следующий символ «b» помещаем в строку В. На этот момент стек и строка В выглядят следующим образом:
В = ”ab”
+
Следующий символ «*». Элемент в вершине стека имеет более низкий приоритет, чем «*», поэтому в строку В ничего не помещаем, а «*» помещаем в стек. Далее идет символ «с», он помещается в строку В. После этого имеем:
В = ”abс”
*
+
Следующий символ в строке S «+». Анализируем стек и видим, что элемент в вершине стека «*» имеет более высокий приоритет, чем «+». Поэтому извлекаем этот элемент из стека и помещаем в строку В.
Следующий элемент стека «+» имеет тот же приоритет, что и текущий символ строки S. Следовательно, извлекаем элемент из стека и помещаем его в строку В, а прочитанный из строки S элемент помещаем в стек. В итоге имеем:
В = ”abс*+”
+
В строке S следующий символ «(». Он имеет самый высокий приоритет и помещается в стек. Читаем символ «d» и помещаем в строку В.
В = ”abс*+d”
(
+
Читаем строку S дальше – это символ «*». Так как открывающую скобку нельзя извлечь из стека до тех пор, пока не встретилась закрывающая, то в строку В ничего не помещаем, а знак «*» помещаем в стек. Следующий символ строки S «e» помещаем в строку В.
138
В = ”abс*+de”
*
(
+
Следующий прочитанный символ «+». Так как элемент «*» имеет более высокий приоритет, то извлекаем его из стека и помещаем в строку В. Символ «+» помещаем в стек, а следующий символ строки S «f» помещаем в строку В.
В = ”abс*+de*f”
+
(
+
Далее в строке S идет закрывающая скобка. В этом случае все элементы стека до символа «)» включительно помещаем в строку В (это элемент «+»). Символ «(» просто игнорируется после того, как был извлечен из стека, и читается очередной символ входной строки S.
В = ”abс*+de*f+”
+
Читаем символ «*», помещаем его в стек, а следующий за ним символ «g» – в строку В.
В = ”abс*+de*f+g”
*
+
Закончив чтение символов строки S, переписываем элементы из стека в строку В.
В = ”abс*+de*f+g*+”
Таким образом, просмотрев исходную информацию только один раз, мы решили поставленную задачу.
Пример 2. Пусть задано выражение, записанное в постфиксной форме А=”6523+8*+3+*”, операндами которого являются цифры. Вычислить его значение.
Решение. В постфиксной записи каждая операция относится к двум предшествующим операндам. Причем один из этих операндов может быть результатом операции, выполненной ранее.
Записываем в стек каждый встретившийся операнд.
Если встречается операция, то ее операндами будут два верхних элемента
стека.
Извлекаем эти элементы, выполняем над ними текущую операцию, и результат помещаем в стек.
139
Выполнение алгоритма на примере
В начале организуем пустой стек.
Первые четыре символа выражения – операнды, читаем их и помещаем в стек.
Следующий элемент «+». Извлекаем из стека соответствующие операнды («3» и «2»), выполняем действие 3+2, результат «5» помещаем в стек.
Далее в стек помещаем очередной операнд входной строки «8».
3
2
5
6
5
5
6
8
5
5
6
Теперь встретился знак операции «*». Извлекаем из стека для него операнды «8» и «5», выполняем умножение 8*5, результат «40» помещаем в стек.
Следующим символом идет «+». Извлекаем из стека «40» и «5», выполняем сложение операндов 40+5, результат «45» помещаем в стек.
Читаем и помещаем в стек очередной операнд входной строки
«3».
40
5
6
45
6
3
45
6
Следующий символ строки А «+». Извлекаем из стека операнды для этой операции («3» и «45») и выполняем сложение 3+45, результат «48» помещаем в стек.
48
6
Последний символ в строке А «*». Операнды для этой операции – «48» и «6». В стек помещаем результат выполнения этой операции – 48*6=288, это и есть значение заданного выражения.
Пример реализации алгоритма получения обратной польской записи на основании приоритета операций, который предложен Дейкстрой.
#include<stdio.h>
140
#include<stdlib.h> |
|
#include<conio.h> |
|
#include<string.h> |
|
struct Stack { |
|
char c; |
|
Stack *Next; |
|
} ; |
|
int Prior (char); |
|
void main () { |
|
Stack *t; |
|
char a, In[50], Out[50]; |
// Входная и выходная строки |
Stack *Op = NULL; |
// Стек операций Op – пуст |
int k, l; |
// Текущие индексы для строк |
puts(" Input formula : "); |
|
gets(In); |
|
k=l=0; |
|
while ( In[k] != '\0') { |
|
//================= Часть 1 ==============================
if ( In[k] == ')' ) { |
// Если очередной символ ")", выталкиваем из |
||
|
// стека все знаки операций в выходную строку |
||
while ( (Op -> c) != '(' ) { |
// до первой открывающей скобки "(" |
||
t = Op; |
// Заносим в него вершину стека |
||
a = t -> c; |
// B а записываем значение элемента вершины |
||
Op = t -> Next; |
// В вершину заносим адресную часть |
||
delete t; |
// Сняли указатель с элемента (извлекли) |
||
if ( !(Op) ) a = '\0'; |
|
|
|
Out[l++] = a; |
// Информационную часть – в выходную строку |
||
} |
|
|
|
t = Op; |
|
// Удаляем из стека открывающуюся скобку |
|
Op = t -> Next; |
|
|
|
if ( Op = = NULL ) { |
// Стек пустой |
||
puts (" End of Stack!"); |
|
||
break; |
|
|
|
} |
|
|
|
delete t;
}
//====================== Часть 2 =========================
if ( (In[k] >= 'a') && (In[k] <= 'z')) |
// Если символ буква, |
|
Out[l++] = In[k]; |
// то заносим ее в выходную строку |
|
//====================== Часть 3 ========================= |
||
if ( In[k] == '(' ) { |
// Если символ входной строки открывающаяся |
|
t = new Stack; |
// скобка, то заталкиваем ее в стек |
|
|
|
|
t -> c = In[k]; |
|
|
t -> Next = Op; |
|
|
141
Op = t;
}
//======================== Часть 4 ========================
if ( In[k] == '+' || In[k] == '–' || In[k] == '*' || In[k] == '/') {
//Если знак операции, то переписываем в выходную строку все операции, while ( (Op !=NULL) && (Prior (Op -> c) >= Prior (In[k]))) {
//находящиеся в стеке с большим или равным приоритетом
t = Op;
a = t -> c;
Op = t -> Next;
delete t; // Извлекли элемент из стека
// if ( !(Op) ) a = '\0'; Out[l++] = a;
|
} |
|
|
t = new Stack; |
// Записываем в стек поступившую информацию |
|
t -> c = In[k]; |
|
|
t -> Next = Op; |
|
} |
Op = t; |
|
k++; |
|
|
|
|
|
} |
// Конец цикла анализа входной строки |
|
//======================== Часть 5 =======================
while ( Op !=NULL) { // После рассмотрения всей входной информации
t = Op; |
// переписываем операции из стека |
a = t -> c; |
// в выходную строку |
Op = t -> Next; delete t; Out[l++] = a;
}
Out[l] = '\0';
printf("\n Polish = %s", Out); // Печатаем полученную строку getch();
}
//========= Функция реализации приоритета операций ============
int Prior ( char a ) { switch ( a ) {
case '*': case '/': return 3; case '–': case '+': return 2; case '(': return 1;
}
return 0;
}
142