
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
- •6. 14 Длина волны де Бройля___________________________________________________
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
6.2.10. Потенциальный барьер конечной ширины.
ТУННЕЛЬНЫЙ ЭФФЕКТ
6.49 Потенциальный барьер конечной ширины___________________________________

[U0 — высота потенциального барьера; Е — полная энергия частицы; m — масса частицы]
6.50 Энергия частицы больше высоты потенциального барьера_____________________
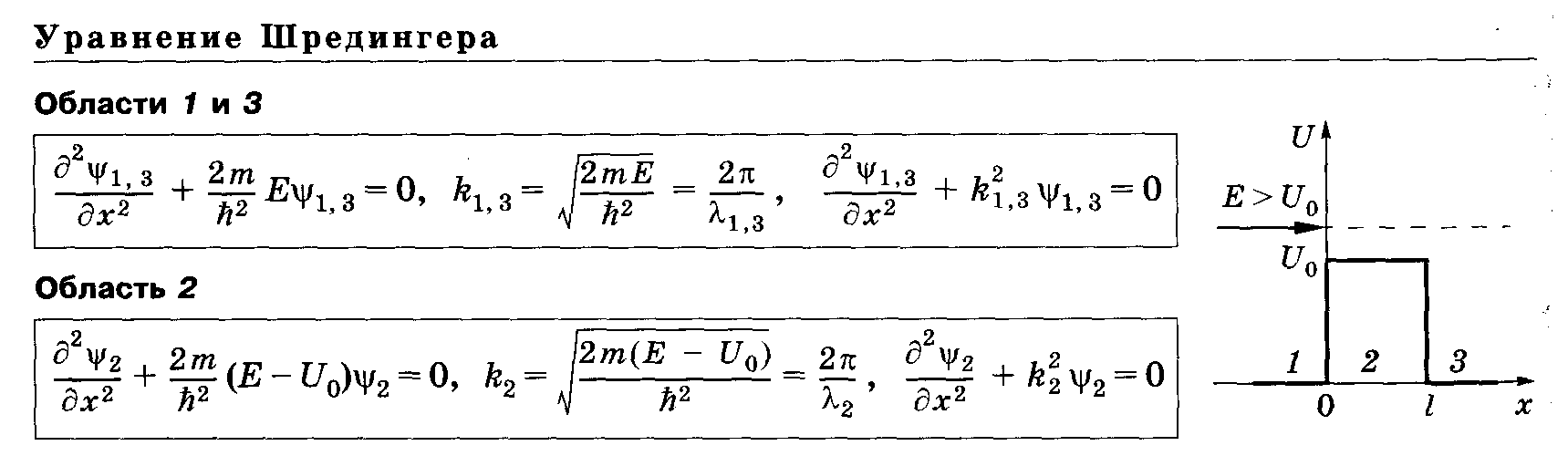
[k1,3
=
![]() иk2
=
иk2
=
![]() —
волновые числа; λ 1,
3
и
λ2
—
соответственно длины волн
де Бройля в областях 1,
3 и 2]
—
волновые числа; λ 1,
3
и
λ2
—
соответственно длины волн
де Бройля в областях 1,
3 и 2]
Общие решения уравнений Шредингера___________________________________________
В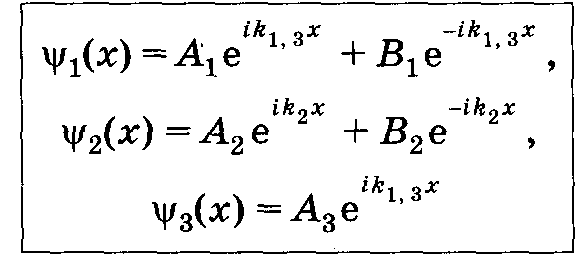 области 3 имеется только прошедшая
барьер волна, поэтому коэффициент В3
принят равным нулю.
области 3 имеется только прошедшая
барьер волна, поэтому коэффициент В3
принят равным нулю.
♦
![]() соответствует
плоской волне, распространяющейся в
положительном
направлении оси х
(падающей
волне), е
-ikx
—
отраженной
волне. О волнах может идти речь после
умножения
на временной множитель, так как Ψ
—
координатная часть
волновой функции.
соответствует
плоской волне, распространяющейся в
положительном
направлении оси х
(падающей
волне), е
-ikx
—
отраженной
волне. О волнах может идти речь после
умножения
на временной множитель, так как Ψ
—
координатная часть
волновой функции.
322
6.51 Возможное определение коэффициентов отражения и прозрачности

Вывод. В
случае Е >U0
волна на
границе 1 и
2 частично
отражается (![]() и
частично проходит в область 2,
затем она
опять на границе 2
и 3 частично
отражается (
и
частично проходит в область 2,
затем она
опять на границе 2
и 3 частично
отражается (![]() )
и частично проходит в область3.
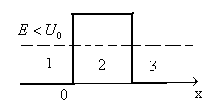
В области
2 (см.
рисунок 6.50)
длина волны де Бройля больше, чем в
областях 1 и
З.
)
и частично проходит в область3.
В области
2 (см.
рисунок 6.50)
длина волны де Бройля больше, чем в
областях 1 и
З.
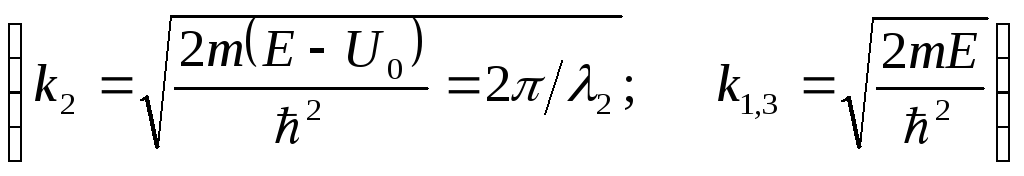
Итак, при E > U0 имеем k1,3 > k2 и λ2 > λ1,3
6.52 Энергия частицы
меньше высоты потенциального барьера (Е < U0)_____________________________
Уравнение Шредингера_________________________________________________________
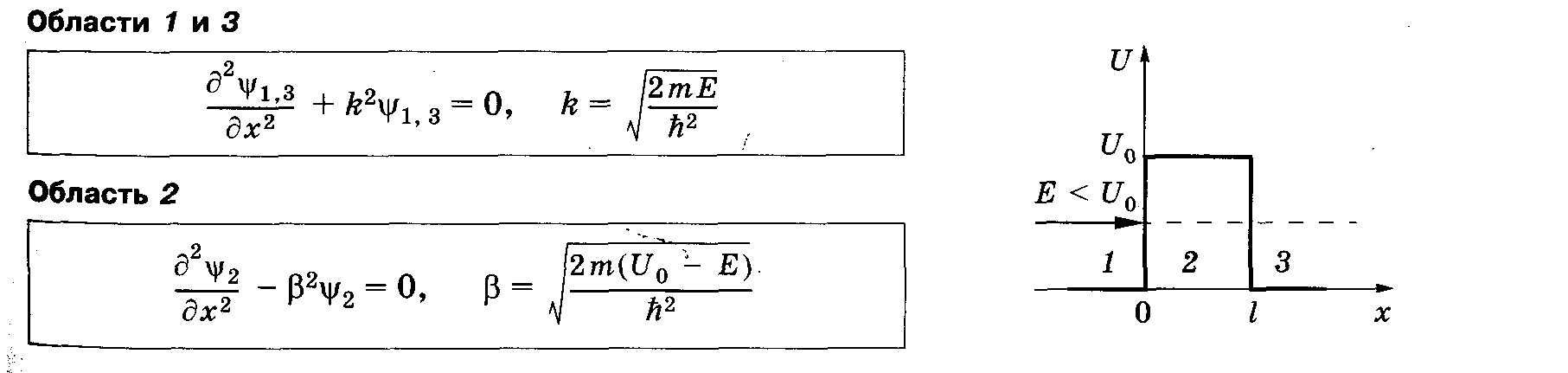
Общие решения уравнений Шредингера__________________________________________
В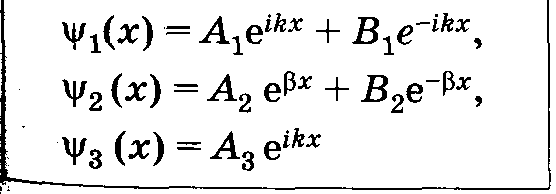 области2
решение Ψ2
(х) не
соответствует плоским волнам,
распространяющимся в обе стороны
(показатели экспонент не мнимые, а
действительные).
области2
решение Ψ2
(х) не
соответствует плоским волнам,
распространяющимся в обе стороны
(показатели экспонент не мнимые, а
действительные).
♦ В области 3
имеется только волна, прошедшая сквозь
барьер и распространяющаяся слева
направо, поэтому принято В3
= 0. Из условий непрерывности волновой
функции и ее первой производной в точках
х = 0
и х =
![]() можно найти
коэффициенты А2
и В2.
Можно
показать, что для высокого и широкого
барьера
можно найти
коэффициенты А2
и В2.
Можно
показать, что для высокого и широкого
барьера
![]() »1) В2
» А2,
а тогда на
границе потенциального барьера, где х
= 0, опреде ляющим
членом волновой функции Ψ2
является член, содержащий В2
»1) В2
» А2,
а тогда на
границе потенциального барьера, где х
= 0, опреде ляющим
членом волновой функции Ψ2
является член, содержащий В2
![]() .
.
Вывод. В случае Е < U0, согласно квантовой механике, микрочастица может «пройти» сквозь потенциальный барьер. Это специфическое квантовое явление получило название туннельного эффекта.
6.53 Туннельный эффект________________________________________________________________
Волновые функции в областях 1, 2 и 3_________________________________________________
|
|
6.52
 Выводы.
Волновая
функция не равна нулю и внутри барьера,
а в области 3, если барьер не очень широк,
будет опять иметь вид волн де Бройля с
тем же импульсом, т. е. с той же частотой,
но с меньшей амплитудой. Следовательно,
частица имеет отличную от нуля вероятность
прохождения сквозь потенциальный
барьер конечной ширины — наблюдается
туннельный
эффект.
Выводы.
Волновая
функция не равна нулю и внутри барьера,
а в области 3, если барьер не очень широк,
будет опять иметь вид волн де Бройля с
тем же импульсом, т. е. с той же частотой,
но с меньшей амплитудой. Следовательно,
частица имеет отличную от нуля вероятность
прохождения сквозь потенциальный
барьер конечной ширины — наблюдается
туннельный
эффект.
6.54 Коэффициент прозрачности для прямоугольного барьера______________________
Коэффициент прозрачности (вероятность проникновения
сквозь потенциальный барьер конечной ширины) ___________________________
![]() D
быстро убывает с увеличением ширины
барьера, а также с ростом его высоты.
D
быстро убывает с увеличением ширины
барьера, а также с ростом его высоты.
[U0
— высота потенциального барьера; Е
—
энергия частицы;
![]() —
ширина прямоугольного барьера; т
—
масса частицы;
—
ширина прямоугольного барьера; т
—
масса частицы;
![]() —
постоянная Планка; D0
—
постоянный
множитель, который, как показывают
точные расчеты, не очень отличается
от единицы]
—
постоянная Планка; D0
—
постоянный
множитель, который, как показывают
точные расчеты, не очень отличается
от единицы]
