Элементы квантовой механики

ГИПОТЕЗА ДЕ БРОЙЛЯ. ВОЛНЫ ДЕ БРОЙЛЯ

Универсальность корпускулярно-волнового дуализма

______________________________________________________________________________________

Гипотеза де Бройля_______________________________________________________________

Корпускулярно-волновой дуализм имеет универсальный характер и распространяется не только на фотоны, но и на все частицы материи: частицы вещества (в частности, электроны) обладают наряду с корпуску­лярными также и волновыми свойствами.

Уравнения, связывающие корпускулярные свойства (энергия и импульс) и волновые (частота (длина волны)) характеристики микрочастиц_____________________________

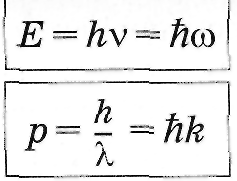Формулы такие же, что и для фотона.

[к — волновое число; постоянная Планка;циклическая частота]

Длина волны де Бройля___________________________________________________

[h — постоянная Планка; р — импульс; т — масса частицы; υ — скорость части­цы; Т — кинетическая энергия частицы; с — скорость распространения света в вакууме; Е — полная энергия частицы]

6. 15 Экспериментальное подтверждение

волновых свойств микрочастиц_____________________________________________

Опыты Девиссона и Джермера___________________________________________________

Пучок электронов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, дает отчетливую дифракционную карти­ну. Дифракционные максимумы соответствовали формуле Вульфа— Брэггов 5.50, а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле X = Н/р.

Опыты Тартаковского и Томсона________________________________________________

Наблюдалась дифракционная картина при прохождении пучка быстрых электронов (« 50 кэВ) через металлическую фольгу (толщиной » 1 мкм).

Опыты Тартаковского__________________________________________________________

Даже в случае столь слабого электронного пучка, когда каждый элект­рон проходит через прибор независимо от других (промежуток времени между двумя электронами в 10⁴ раз больше времени прохождения элект­роном прибора), возникающая при длительной экспозиции дифракцион­ная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз

308

более интенсивных. Следовательно, волновые свойства частиц не являют­ся свойством их коллектива, а присущи каждой частице в отдельности.

♦ Дифракционные явления обнаружены также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля.

6. 16 Плоская волна де Бройля_________________________________________________________

Согласно корпускулярно-волновому дуализму материи и гипо­тезе де Бройля, с движением частицы, обладающей определенны­ ми энергией и импульсом, связывается плоская волна де Бройля.

Рассмотрен одномерный случай. Уравнение плоской волны, распространяющейся вдоль оси х, имеет вид или в комплексной записи. При записи плоской волны де Бройля учтено, что (ω — циклическая частота,k — волновое число). Показатель экспоненты в плоской волне де Бройля берется со знаком минус, но это несущественно, так как физический смысл имеет 6.22 .

6. 17 Свойства волн де Бройля _____________________________________

Фазовая скорость 4.47______________________________________________

Дисперсия волн де Бройля______________________________________________________

нерелятивистский случай

Фазовая скорость, как для нерелятивистских, так и релятивистских частиц, зависит от длины волны (частоты), поскольку релятивистский случай

[ω — циклическая частота; k — волновое число; — постоянная Планка;Е — полная энергия частицы; р — импульс частицы; υ — скорость движения частицы; с — скорость распространения света в вакууме; т — масса частицы]

6.2.2. Соотношение неопределенностей гейзенберга

Во многих случаях классические представления (например, в каждый момент времени частица занимает в пространстве строго определенное 1 место и обладает определенным импульсом) неприменимы для описания микрообъектов. Гейзенберг выдвинул идею о принципиальной невоз­можности измерения определенных пар связанных между собой харак­теристик так, чтобы они одновременно имели точные значения.

6.18 Соотношение неопределенностей для координат и импульсов_______

М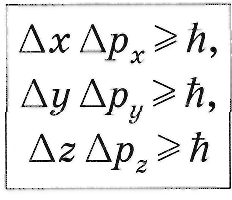икрочастица (микрообъект) не может иметьодновременно точных зна­чений координаты (х, у, z) и соответствующих компонентов импульса (), причем произведение неопределенностей координаты и соот­ветствующей ей проекции импульса не может быть меньше величины порядка .

Физический смысл соотношения____________________________________________

Из соотношения неопределенностей следует, что, например, если микро­частица находится в состоянии с точным значением координаты (), то в этом состоянии соответствующая проекция ее импульса оказываетсясовершенно неопределенной (), и наоборот. Таким образом, длямикрочастицы не существует состояний, в которых ее координаты и им­пульс имели бы одновременно точные значения.

6.19 Соотношение неопределенностей для энергии и времени______________

[— неопределенность энергии некоторого состояния системы; — промежуток времени, в течение которого оно существует]

Физический смысл соотношения _____________ _________________

Из-за конечности времени жизни атомов в возбужденном состоянии энер­гия возбужденных состояний атомов не является точно определенной, поэтому частота излученного фотона также должна иметь неопределен­ность . Тогда линии спектра должны иметь частоту . Опыт действительно показывает, что все спектральные линии размыты.

6.20 Соотношение неопределенностей — следствие

специфики микрообъектов _________

Невозможность одновременно точно определить координату и соответст­вующую проекцию импульса не связана с несовершенством методов из­мерения или измерительных приборов, а является следствием специфи­ки микрообъектов, отражающей особенности их объективных свойств, а именно двойственной корпускулярно-волновой природы. Соотношение неопределенностей получено при одновременном использовании класси­ческих характеристик движения частицы (координаты, импульса) и на­личия у нее волновых свойств. Так как в классической механике прини­мается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является, та­ким образом, квантовым ограничением применимости классической механики к микрообъектам.

♦ Повышение точности в знании одной переменной, таким образом, ведет к понижению точности в знании другой, и наоборот. Поэтому если в клас­сической механике наличие координат и импульсов (скоростей) системы точно задает ее поведение во времени и пространстве, то предсказание поведения квантовой системы должно носить вероятностный характер.

310

6.2.3. ВОЛНОВАЯ ФУНКЦИЯ И ЕЕ СТАТИСТИЧЕСКИЙ СМЫСЛ

В общем случае (произвольное движение частицы в произвольных силовых полях) состояние частицы в квантовой механике задается волновой е функцией (или пси-функцией) ,зависящей от координат и времени. Она — основной носитель информации о корпускулярных и волновых свойствах микрочастиц. В частном случае свободного движения частицы волновая функция — плоская волна де Бройля 6.16 .