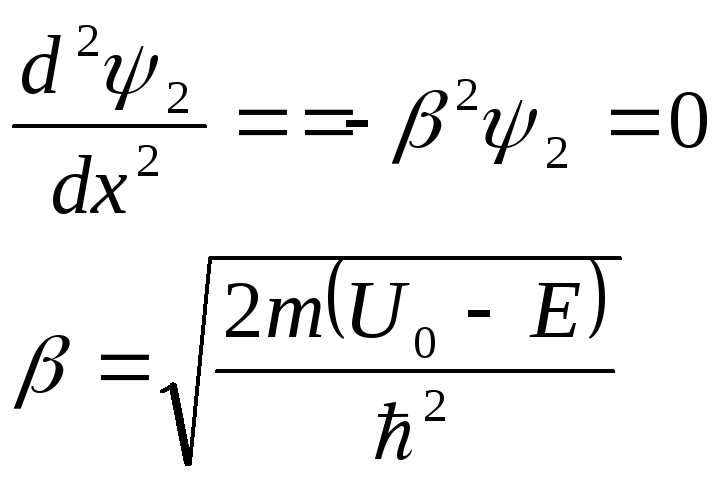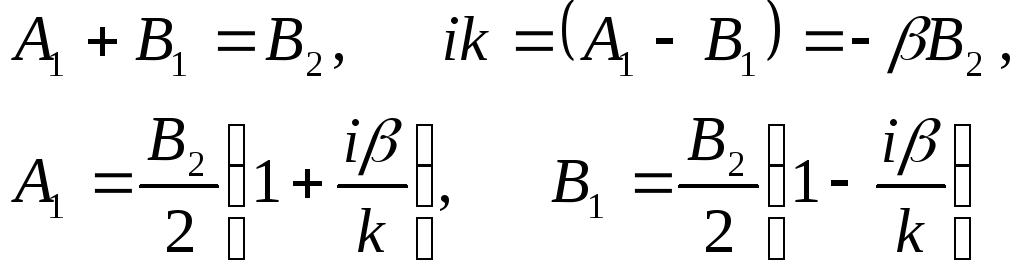- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
- •6. 14 Длина волны де Бройля___________________________________________________
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
6.41 Энергетический спектр частицы_______________________________________________
Собственные значения энергии частицы_______________________________________________

![]() и
и![]() .Спектр энергии частицы
дискретен. Квантованные
значения Еп
– уровни
энергии, п
— квантовое
число.
.Спектр энергии частицы
дискретен. Квантованные
значения Еп
– уровни
энергии, п
— квантовое
число.
Минимальная, не равная нулю энергия,
соответствующая основному состоянию_______________________________________________
_![]() ____________
____________
Наличие отличной
от нуля минимальной энергии — следствие
соотношения неопределенностей 6.18.
Неопределенность импульса
![]() (частица «зажата» в яме, следовательно,
ее положение известно с неопределенностью
(частица «зажата» в яме, следовательно,
ее положение известно с неопределенностью![]() ). Поэтому энергия нулю не может быть
равна (это потребовало бы выполнения
условия
). Поэтому энергия нулю не может быть
равна (это потребовало бы выполнения
условия![]() ).
).
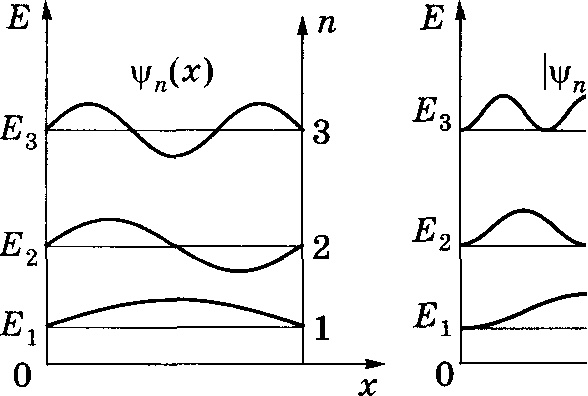
♦ Состояние с энергией Е1 — основное состояние, остальные состояния возбужденные. Энергии возбужденных состояний: 4Е1, 9Е1, 16Е1; ... (соответственно значениям квантовых чисел п = 2, 3, 4, ...) (см. рис. 6.42).
6.42 Собственные функции и плотности вероятности
![]() обнаружения
частицы
обнаружения
частицы
на разных расстояниях от стенок ямы______________________________________________
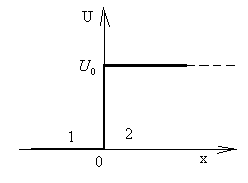
6.2.9. Отражение и прохождение
СКВОЗЬ ПРЯМОУГОЛЬНЫЙ
ПОТЕНЦИАЛЬНЫЙ ПОРОГ
![]()
6.43 Прямоугольный бесконечно протяженный порог______________________________
|
Одномерный потенциальный порог |
Потенциальная энергия |
Стационарное уравнение Шредингера для одномерного случая |
|
|
|
|
[U0 — высота потенциального порога; Е — полная энергия частицы; т – масса частицы]
6.44 Энергия частицы больше высоты порога_(Е > U0)______________________________
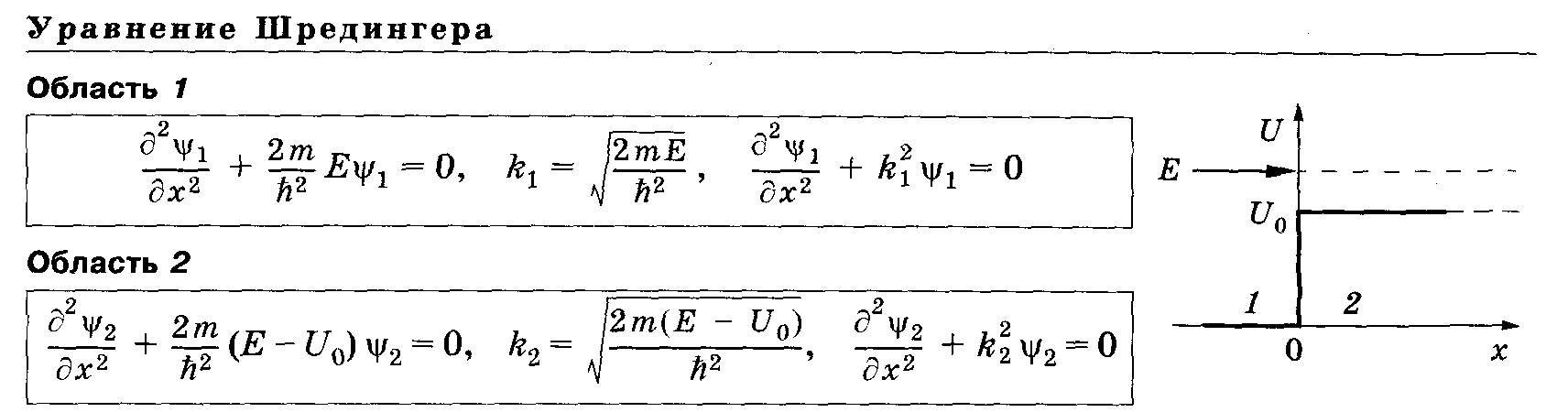
![]() — волновые
числа; λ1
и
λ2
—
соответственно длины волн де
Бройля в областях 1
и 2.]
— волновые
числа; λ1
и
λ2
—
соответственно длины волн де
Бройля в областях 1
и 2.]
Общие решения уравнений Шредингера____________________________________________
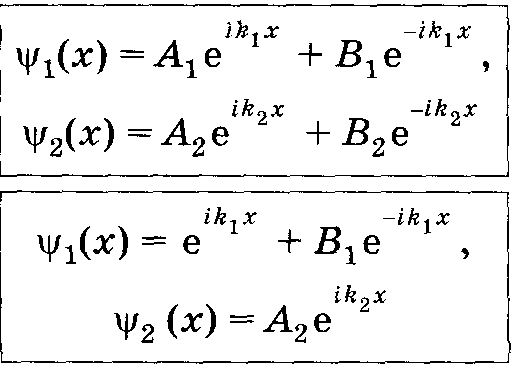
![]() соответствует
плоской волне, распространяющейся в
положительном направлении оси х
(падающей
волне),
соответствует
плоской волне, распространяющейся в
положительном направлении оси х
(падающей
волне),
![]() —отраженной
волне.
—отраженной
волне.
Амплитуда падающей волны принята за единицу (А1 = 1). В области 2 наблюдается только прошедшая волна, поэтому В2 = 0.
♦ О волнах может идти речь после умножения на временной множитель, поскольку Ψ — координатная часть волновой функции.
6.45 Коэффициенты отражения и прозрачности____________________________________
Коэффициент отражения__________________________________________________________
Р![]() авен
отношению плотности потока отраженных
(п\)
частиц к плотнос
ти потока
падающих (n1)
частиц.
авен
отношению плотности потока отраженных
(п\)
частиц к плотнос
ти потока
падающих (n1)
частиц.
Коэффициент прозрачности_______________________________________________________
Р![]() авен
отношению плотности потока прошедших
(тг2)
частиц к плотности
потока
падающих (n1)
частиц.
авен
отношению плотности потока прошедших
(тг2)
частиц к плотности
потока
падающих (n1)
частиц.
Значения n1;
![]() ;
п2
;
п2
![]()
6.46 Определение R и D для случая Е > U0______________________________________________________________
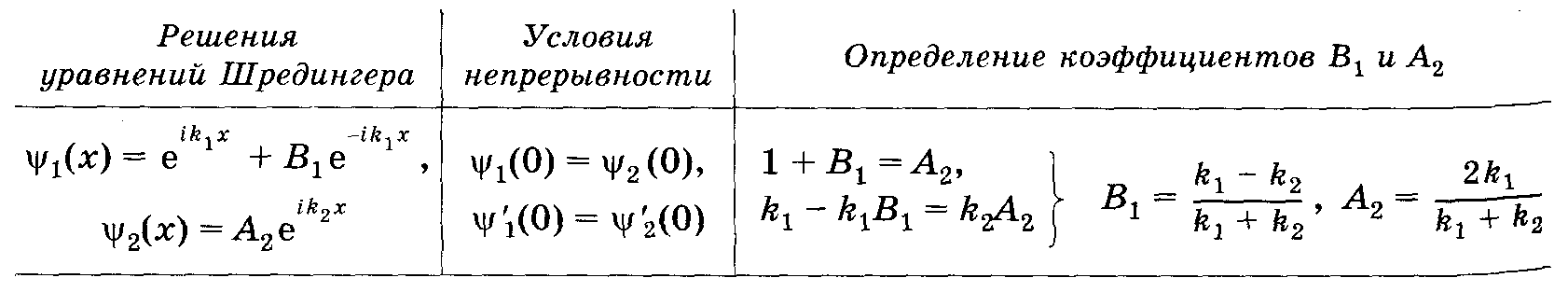
320
Коэффициент отражения___________________________________________________________
![]()
Как п в оптике, R + D = 1. Коэффициент R можно истолковать как вероятность отражения на границе областей, а D — вероятность преодоления потенциального порога. Тогда можно утверждать, что частица либо отразится, либо пройдет в область 2.
Коэффициент прозрачности
![]()
Вывод. В случае Е > U0 (низкий потенциальный порог) волна частично отражается (коэффициент В1 отличен от нуля) и частично проходит в область 2. В области 2 длина волны де Бройля больше, чем в области 1.
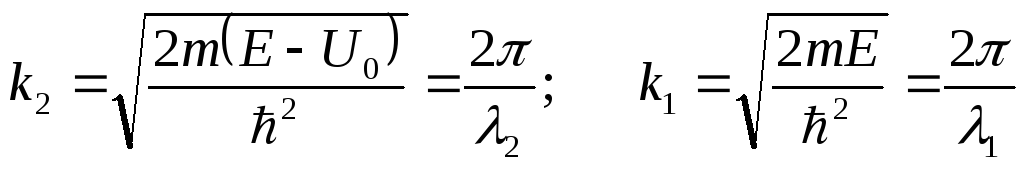
Итак, при Е > U0 волновое число к1> к2 и длина волны λ2 > λ.1.
6.47 Энергия частицы меньше высоты порога (Е < U0)________________________________
|
|
Область 1 |
Область 2 |
|
Уравнение Шредингера |
|
|
|
Общие решения уравнений Шредингера |
|
При
Однако волновая функция по своему физическому смыссвоему физическому смыслу должна оставаться должна оставаться конечной при всех значениях. Следопри всех значениях. Следовательно, нужно принять А2 = 0 |
|
|

6.48 Определение коэффициента отражения R для случая Е < U0
|
Решение уравнений Шредингера |
Условия непрерывности |
Определение коэффициентовА1 и В1 |
|
|
|
|
Коэффициент отражения 6.46_______________________________________________________
|
При Е < U0 коэффициент отражения равен единице, т. е. отражение частиц будет полным.
|
Вероятность найти частицу на единице длины в области 2_________________________
![]()
![]() ,
т. е. в случае
Е < U0
,
т. е. в случае
Е < U0
(высокий прямоугольный потенциальный порог), хотя и наблюдается явление полного отражения, имеется отличная от нуля вероятность найти частицу в области 2, правда, она экспоненциально убывает с увеличением х. Микрочастица благодаря своим волновым свойствам может проникать в области, «запрещенные» для классических частиц.