
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
- •6. 14 Длина волны де Бройля___________________________________________________
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
6.59 Плотности вероятности обнаружения частицы______________________________
П редставлены
кривые распределения плотности
вероятности |\|/п(х)|2
для различных состояний квантового
осциллятора (для п
= 0,
1 и 2). В точках А и А', Вй В',
С и С ‘
потенциальная
энергия равна полной энергии (U
= Е), причем,
как известно, классический осциллятор
не может выйти за пределы этих точек.
Для квантового осциллятора
редставлены
кривые распределения плотности
вероятности |\|/п(х)|2
для различных состояний квантового
осциллятора (для п
= 0,
1 и 2). В точках А и А', Вй В',
С и С ‘
потенциальная
энергия равна полной энергии (U
= Е), причем,
как известно, классический осциллятор
не может выйти за пределы этих точек.
Для квантового осциллятора
![]() и за пределами
этих точек имеет конечные значения.
Последнее означает, что имеется конечная,
хотя и небольшая, вероятность обнаружить
частицу за пределами потенциальной
ямы.
Область, запрещенная
и за пределами
этих точек имеет конечные значения.
Последнее означает, что имеется конечная,
хотя и небольшая, вероятность обнаружить
частицу за пределами потенциальной
ямы.
Область, запрещенная
Этот результат не противоречит выводам квантовой классической механикой
механики, так как равенство Т = Е -U в квантовой механике не имеет силы, поскольку кинетическая (Т) и потенциальная (U) энергии не являются одновременно измеримыми величинами
.
6.60 Плотности вероятности
для квантового и классического осцилляторов___________________________________
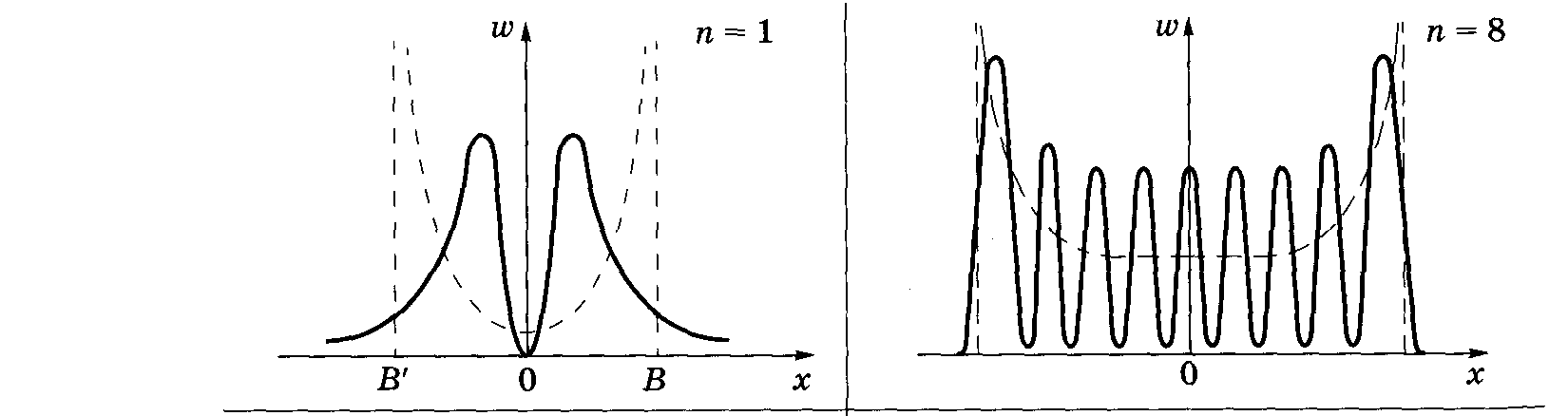
На рисунке — кривая распределения При больших значениях п квантовое рас- плотности вероятности для кванто- пределение плотности вероятности (сплош- вого (сплошная кривая) и классиче- ная кривая) принимает все большее сход- ского (пунктир) осциллятора. Поведе- ство с классическим распределением плот- ние квантового осциллятора значи- ности вероятности (пунктир). В этом про- тельно отличается от классического является принцип соответствия Бора
Принцип соответствия Бора _____
Выводы и законы квантовой механики при больших значениях квантовых чисел должны соответствовать выводам и законам классической физики.
Ниже приведены примерные экзаменационные вопросы по теме «ЭЛЕМЕНТЫ КВАНТОВОЙ МЕХАНИКИ»
В чем суть гипотезы де Бройля?
Какими эксперименты подтверждают волновые свойства микрочастиц? Обладают ли волновыми свойствами движущиеся нейтроны?
Протон и электрон движутся с одинаковыми скоростями. Сравнить их дебройлевские длины волн.
Как изменится длина волны де Бройля летящего протона при уменьшении его скорости?
Определить длину волны де Бройля для электрона с кинетической энергией 2∙10-14 Дж, считая его нерелятивистским. Масса электрона 9,1∙10-31 кг.
Определить длину волны де Бройля для электрона с кинетической энергией 10 КэВ.
«Туннельный» эффект свойственен для микрочастиц
а) классических б) квантовых в) классических и квантовых г) нельзя ответить без дополнительных данных
Высоту потенциального барьера микрочастицы можно измерять в …. (указать ед. измерения).
Протон и электрон, имеющие одинаковые полные энергии Е должны преодолеть высокий потенциальный барьер U > Е. У какой частицы вероятность прохождения барьера больше ?
Из каждой 1000 частиц 100 преодолевают высокий потенциальный барьер. Коэффициент отражения барьера равен … .
При увеличении неопределенности координаты микрочастицы ее неопределенность скорости
А) увеличивается Б) уменьшается В) не изменяется С) нельзя ответить без дополнительных условий
Микрочастица находится в одномерной потенциальной яме шириной 10 мкм на втором энергетическом уровне. В каких точках ямы вероятность нахождения частицы равна нулю?
Микрочастица находится в бесконечно глубокой одномерной потенциальной яме шириной l на пятом энергетическом . В каких точках ямы вероятность обнаружения частицы минимальна?
 Для микрочастицы
в потенциальной яме шириной l,
ψ(х)-функция
имеет вид, представленный на рисунке.
На каком энергетическом уровне находится
частица?
Для микрочастицы
в потенциальной яме шириной l,
ψ(х)-функция
имеет вид, представленный на рисунке.
На каком энергетическом уровне находится
частица? Для микрочастицы в потенциальной яме шириной l, ψ(х)-функция имеет вид, представленный на рисунке. Сравнить вероятности нахождения частицы в интервале 0 ÷ l/2 и 0 ÷ l/3 . Дать пояснения.
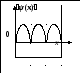 Для микрочастицы
в потенциальной яме шириной l,
ψ(х)-функция
имеет вид, представленный на рисунке.
Сравнить вероятности нахождения частицы
в интервале 0 ÷ l/2
и 0 ÷ l/3
. Дать пояснения.
Для микрочастицы
в потенциальной яме шириной l,
ψ(х)-функция
имеет вид, представленный на рисунке.
Сравнить вероятности нахождения частицы
в интервале 0 ÷ l/2
и 0 ÷ l/3
. Дать пояснения. Известно, что энергия микрочастиц, находящихся в бесконечно глубокой одномерной потенциальной яме шириной l на n -ом энергетическом уровне, определяется выражением
Еn = (n2 π2h2)/ (2ml2).
О пределить
минимальную энергию частицы в яме
шириной 2l,
если ее минимальная энергия в яме шириной
l
составляет 9 МэВ.
пределить
минимальную энергию частицы в яме
шириной 2l,
если ее минимальная энергия в яме шириной
l
составляет 9 МэВ.
На рисунке представлен вид функции для микрочастицы в потенциальной яме. Какое главное квантовое число соответствует изображенной ситуации?
На рисунке приведен вид ψ - функции для микрочастицы, находящейся в одномерной потенциальной яме. Какому энергетическому уровню соответствует эта функция?
На рисунке приведен вид ψ - функции для микрочастицы, находящейся в одномерной потенциальной яме. Вероятность обнаружения частица в точке с координатой х = l равна … (число).
На рисунке представлен вид функции для микрочастицы в потенциальной яме. Какое главное квантовое число соответствует изображенной ситуации?
Д
 ля
микрочастицы в потенциальной яме
ширинойl,
ψ(х)-функция
имеет вид, представленный на рисунке.
Сравнить вероятности нахождения частицы
в интервале 0 ÷ l/2
и 0 ÷ l/3
. Дать пояснения.
ля
микрочастицы в потенциальной яме
ширинойl,
ψ(х)-функция
имеет вид, представленный на рисунке.
Сравнить вероятности нахождения частицы
в интервале 0 ÷ l/2
и 0 ÷ l/3
. Дать пояснения.
Н
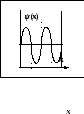 а
рисунке приведен видψ
- функции для микрочастицы, находящейся
в одномерной потенциальной яме. Какому
энергетическому уровню соответствует
эта функция?
а
рисунке приведен видψ
- функции для микрочастицы, находящейся
в одномерной потенциальной яме. Какому
энергетическому уровню соответствует
эта функция? На рисунке приведен вид ψ - функции для микрочастицы, находящейся в одномерной потенциальной яме. Вероятность обнаружения частица в точке с координатой х = l равна … (число).
