6.21 Статистическая интерпретация волновой функции_________________

На основании статистической интерпретации вероятность нахождения частицы в момент времени t с координатами х и х + Δх, у и у + Δу, г + Δz определяется интенсивностью волновой функции, т. е. квадратом пси-функции. Поскольку в общем случае Ψ — комплексная функция а вероятность должна быть всегда действительной и положительной величиной, то за меру интенсивности принимается квадрат модуля во волновой функции.

[Ψ* — функция, комплексно сопряженная Ψ]

6.22 Физический смысл ψ-функции________________________________

Вероятность А\У нахождения частицы в элементе объем в момент времени I.

Плотность вероятности,т. е. вероятность нахождения частицы в момент времени t в окрестности данной точки пространства. Плотность вероятности — величина, наблюдаемая на опыте, в то время как сама волновая функция, являясь комплексной, наблюдению недоступна. В этом заключается существенное отличие в описании состояний частиц в квантовой и классической механике (в классической механике величины, описывающие состояние частиц, наблюдаемы).

Вероятность найти частицу в момент времени t в некотором объеме V.

Условие нормировки вероятностей. Так как dV определяется как вероятность, то, проинтегрировав это выражение в бесконечных пределах, получим вероятность того, что частица в момент времени t находится где-то в пространстве. Это есть вероятность достоверного события, а ее в теории вероятностей считают равной 1.

♦ Волновая функция — объективная характеристика состояния микрочастиц должна удовлетворять ряду ограничений. Она должна быть конечной (вероятность не может быть больше единицы), однозначной (вероятность не может быть неоднозначной величиной) и непрерывной (вероятность не может изменяться скачком)

6.23 Принцип суперпозиции состояний для волновых функций_________

Если какая-либо система (частица или их совокупность) может находиться в различных состояниях, описываемых волновыми функциями Ψ'₁, Ψ₂, ... , Ψ_п, ... , то она может находиться в состоянии Ψ, описываемом линейной комбинацией этих функций.

[С_п (п = 1, 2, ...) — произвольные (в общем случае комплексные) числа, при этом квадрат модуля коэффициента С _n, т. е. |С_n|², равен вероятности обнаружить, что система, представленная состоянием Ψ, может оказаться в состоянии Ψ _n. Сложение волновых функций (амплитуд вероятностей), а не вероятностей (определяемых квадратами модулей волновых функций) принципиально отличает квантовую теорию от классической статистической теории, в которой для независимых событий справедлива теорема сложения вероятностей]

6.2.4. ВРЕМЕННОЕ И СТАЦИОНАРНОЕ УРАВНЕНИЯ ШРЕДИНГЕРА

6.24 Основное уравнение нерелятивистской квантовой механики___________________

Статистическое толкование волн де Бройля 6.22 и соотношение неопределенностей Гейзенберга 6.18 привели к выводу, что уравнением движе­ния в квантовой механике, описывающим движение микрочастиц в различных силовых полях, должно быть уравнение, из которого бы вытека­ли наблюдаемые на опыте волновые свойства частиц. Основное уравнение должно быть уравнением относительно волновой функции ЧХх, у, г, I), так как именно она, или, точнее, величина I^х?!², определяет вероятность пребывания частицы в момент времени I в объеме (IV, т. е. в области с координатами х и х + Ах, у иг/ + Ау, гшг + Аг. Так как искомое уравнение должно учитывать волновые свойства частиц, то оно должно быть волновым уравнением, подобно уравнению, описывающему элек­тромагнитные волны.

Временное уравнение Шредингера__________________________________________________

Это уравнение постулируется, а его правильность подтверждается согласием с опытом получаемых с его помощью результатов.

Условия, накладываемые на волновую функцию______________________________________

♦ Волновая функция должна: быть конечной, однозначной и непрерывной.

♦ Производные —должны быть непрерывны.

• Функция |Ψ|² должна быть интегрируема (это условие сводится к усло­вию нормировки вероятностей 6.22).

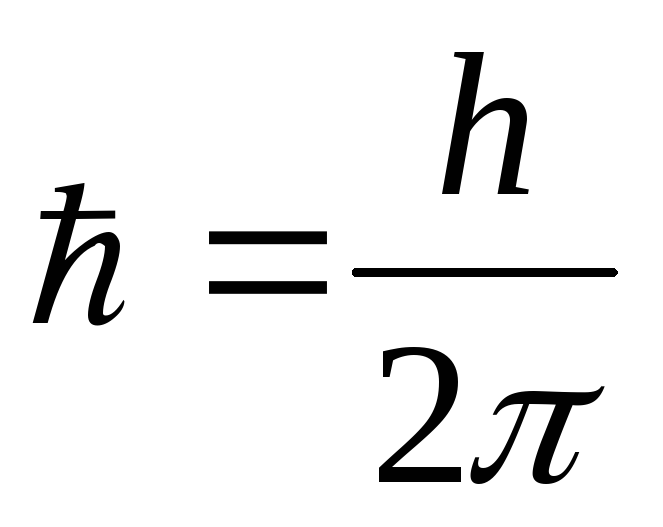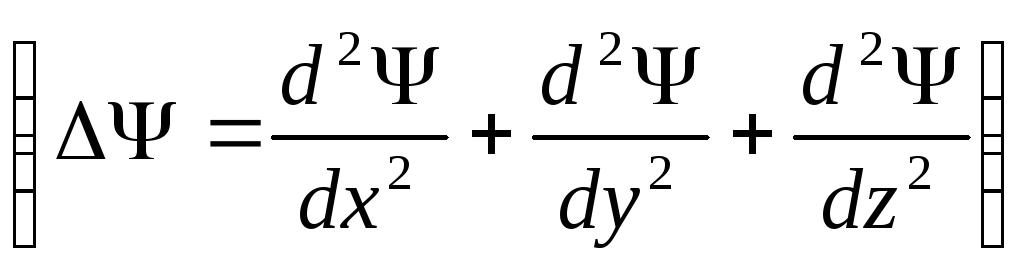• Уравнение Шредингера справедливо для нерелятивистских частиц (скорости υ « с). [,т — масса частицы, Δ — оператор Лапласа ,i - мнимая единица, U(x,y,z,t) — потенциальная функция частицы в силовом поле, в котором она движется, Ψ(x,y,z,t) — искомая волновая функция частицы]