6.55 Коэффициент прозрачности для барьера произвольной формы ___________

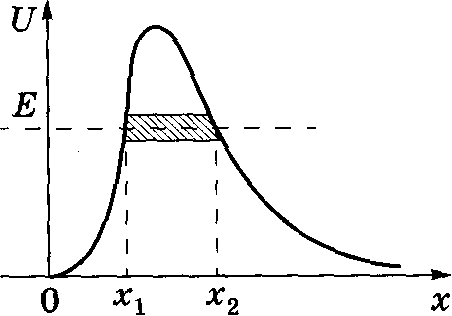
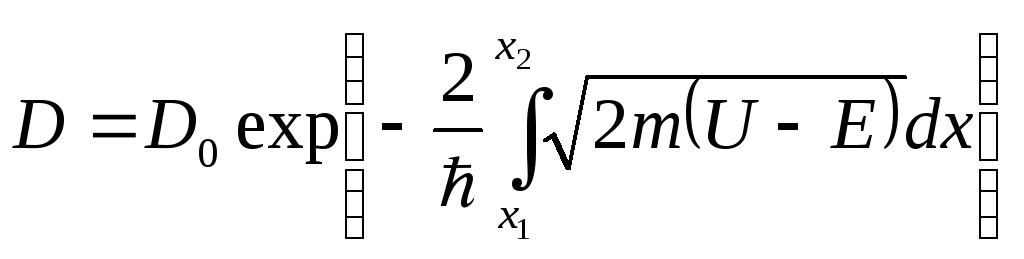
Эта формула — хорошее приближение в случае потенциального барьера произволь­ной формы, если барьер удовлетворяет ус­ловию квазиклассического приближения (достаточно гладкая форма кривой).

♦ Эта формула — обобщение формулы для D в случае прямоугольного барьера.

6.56 Выводы относительно поведения классической

и квантовой частиц_______________________________________________________

При Е < U₀ по классической теории частицы не смогут преодолеть потен­циального барьера и отразятся от него; согласно квантовой теории, часть частиц отражается, а часть имеет отличную от нуля вероятность пройти сквозь потенциальный барьер. При Е > U₀, по классической теории все частицы преодолевают потенциальный барьер; согласно квантовой тео­рии, часть частиц проходит, а часть отражается. Как подбаръерное про­хождение, так и надбарьерное отражение являются специфическими квантовыми эффектами, связанными с волновыми свойствами частиц.

6.2.11. Линейный гармонический осциллятор

Линейный (одномерный) гармонический осциллятор______________________________

Система, совершающая одномерное движение под действием квазиупругой силы. Задача о гармоническом осцилляторе в квантовой теории играет фундаментальную роль по двум причинам: 1) она встречается во всех задачах, где имеют место квантованные колебания (например, в квантовой теории поля, в теории молекулярных и кристаллических колебаний и т. д.); 2) проблемы, относящиеся к гармоническому осциллятору, — хорошая иллюстрация основных принципов и форм квантовой механики.

6.57 Описание гармонического осциллятора в квантовой механике_________________

Потенциальная энергия линейного гармонического осциллятора___________________

Потенциальная яма в данном случае является параболической.

Оператор Гамильтона для осциллятора__________________________________________

6.37

Стационарное уравнение Шредингера в операторной форме________________________

Это уравнение по внешнему виду совпадает с записанным выше уравнением6.38, однако здесь другой оператор.

Уравнение Шредингера для гармонического осциллятора__________________________

Это же уравнение получается при подстановкеU в стационарное уравнение Шредингера 6.25.

[т — масса частицы; ω₀ — собственная частота колебаний осциллятора x - отклонение из положения равновесия; — оператор кинетической энергии;— оператор потенциальной энергии;- постоянная Планка;Е — полная энергия осциллятора; Ψ — координатная часть волновой функции]

6.58 Следствия уравнения Шредингера для квантового осциллятора________________

Собственные значения энергии__________________________________________________

Уравнение Шредингера имеет однозначные, конечные и непрерывные решения только при таких Е_п, т. е. энергия квантового осциллятора может иметь лишь дискретные решения (квантуется).

[ω₀ — собственная частота колебаний осциллятора; — постоянная Планка;Е_п — собственные значения энергии; Е₀ — энергия нулевых колебаний]

Расстояние между соседними уровнями___________________________________________

Уровни энергии линейного гармонического осциллятора расположены на одинаковых расстояниях друг от друга (на рисунке6.59 они изображены горизонтальными прямыми)

Энергия нулевых колебаний___________________________________________________

Ее существованиетипично для квантовых систем; следствие соотношения неопределенностей: частица не может находиться на дне потенциальной ямы независимо от ее формы. Если бы это было возможно, то импульс, а также его неопределенность, обращались бы в нуль. Тогда неопределенность координаты , что противоречит пребыванию час­тицы в потенциальной яме.