
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
- •6. 14 Длина волны де Бройля___________________________________________________
- •6. 15 Экспериментальное подтверждение
- •6. 16 Плоская волна де Бройля_________________________________________________________
- •6. 17 Свойства волн де Бройля _____________________________________
- •6.2.2. Соотношение неопределенностей гейзенберга
- •6.21 Статистическая интерпретация волновой функции_________________
- •6.22 Физический смысл ψ-функции________________________________
- •6.23 Принцип суперпозиции состояний для волновых функций_________
- •6.24 Основное уравнение нерелятивистской квантовой механики___________________
- •6.25 Стационарное уравнение Шредингера________________________________________
- •6.2.5. Операторы в квантовой механике и их свойства
- •6.26 Математический аппарат квантовой механики___________________________________
- •6.27 Свойства операторов_________________________________________________________________
- •6.28 Линейные и эрмитовы операторы_______________________________________________
- •6.29 Свойства собственных функций______________________________________________
- •6.30 Обобщенный ряд Фурье_____________________________________________________
- •6.31 Средние значения физических величин__________________________________________
- •6.32 Возможность одновременного измерения физических величин____________________
- •6.2.6. Операторы важнейших физических величин
- •6.33 Связь между изображением физических величин операторами и опытом____________
- •6.34 Операторы координаты и импульса___________________________________________
- •6.35 Операторы момента импульса______________________________________________________
- •6.36 Уравнения для собственных значений операторов и _______________________
- •6.37 Операторы энергии____________________________________________________________
- •6.38 Уравнение Шредингера в операторной форме__________________________________
- •6.2.7. Движение свободной частицы
- •6.38 Уравнение Шредингера для стационарных состояний ______________________
- •6.39 Потенциальная яма с бесконечно высокими стенками_________________________
- •6.40 Решение уравнения Шредингера для частицы в яме_____________________________
- •6.41 Энергетический спектр частицы_______________________________________________
- •6.42 Собственные функции и плотности вероятности
- •6.2.9. Отражение и прохождение
- •6.43 Прямоугольный бесконечно протяженный порог______________________________
- •6.45 Коэффициенты отражения и прозрачности____________________________________
- •6.2.10. Потенциальный барьер конечной ширины.
- •6.49 Потенциальный барьер конечной ширины___________________________________
- •6.50 Энергия частицы больше высоты потенциального барьера_____________________
- •6.51 Возможное определение коэффициентов отражения и прозрачности
- •6.52 Энергия частицы
- •6.53 Туннельный эффект________________________________________________________________
- •6.54 Коэффициент прозрачности для прямоугольного барьера______________________
- •6.55 Коэффициент прозрачности для барьера произвольной формы ___________
- •6.56 Выводы относительно поведения классической
- •6.2.11. Линейный гармонический осциллятор
- •6.57 Описание гармонического осциллятора в квантовой механике_________________
- •6.58 Следствия уравнения Шредингера для квантового осциллятора________________
- •6.59 Плотности вероятности обнаружения частицы______________________________
- •6.60 Плотности вероятности
6.38 Уравнение Шредингера в операторной форме__________________________________
|
Уравнение |
Обычная запись уравнения |
Гамильтониан, оператор полной энергии |
Операторная форма |
|
Временное уравнение Шредингера |
|
|
|
|
|
Ψ = Ψ(х, у, z, t). Уравнение Шредингера в операторной форме имеет более общий характер и пригодно для описания движения частицы в произвольных стационарных и нестационарных полях, в частности в случае движения частицы в электромагнитном поле | ||
|
Стационарное уравнение Шредингера |
|
|
|
[Е — полная энергия частицы; Ψ = Ψ(х, у, z) — координатная часть волновой функции Ψ(x, y, z, t); стационарное уравнение Шредингера в операторной форме имеет регулярные решения лишь при определенных значениях Е, образующих спектр оператора полной энергии]
6.2.7. Движение свободной частицы
Свободная частица — частица, движущаяся в отсутствие внешних полей. Так как на свободную частицу (пусть она движется вдоль оси х) силы не действуют, то потенциальная энергия частицы U(х) = соnst и ее можно принять равной нулю. Тогда полная энергия частицы совпадает с ее кинетической энергией.
6.38 Уравнение Шредингера для стационарных состояний ______________________
Уравнение Шредингера ______________________
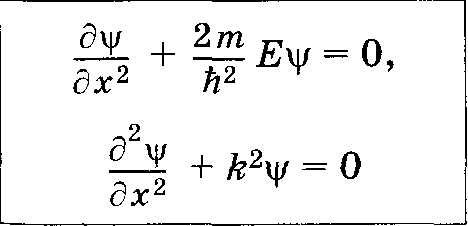
Ψ(х)
= Аe
iкх
=
![]() (А
= const,
к = const);
(А
= const,
к = const);

♦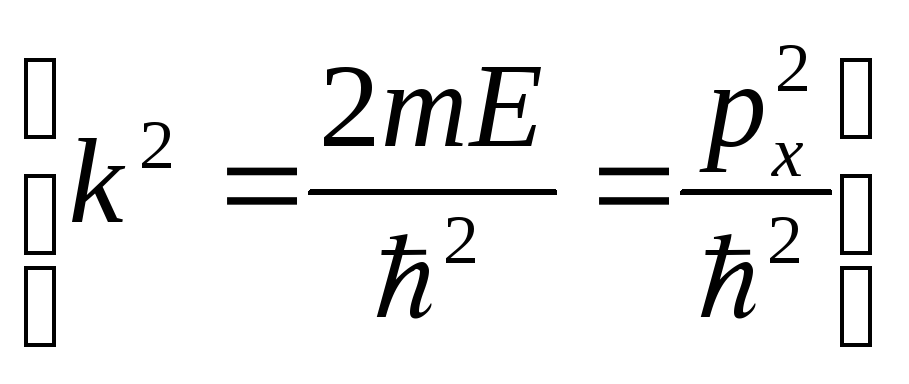 Зависящая
от времени волновая функция Ψ(x,
t)
представляет
собой монохроматическую волну де Бройля
6.16.
Зависящая
от времени волновая функция Ψ(x,
t)
представляет
собой монохроматическую волну де Бройля
6.16.
Собственные значения энергии________________________________________________
Э![]() нергия
свободной частицы может приниматьлюбые
значения (так
как волновое
число k
может
принимать любые положительные значения),
т. е. энергетический
спектр свободной частицы непрерывен.
нергия
свободной частицы может приниматьлюбые
значения (так
как волновое
число k
может
принимать любые положительные значения),
т. е. энергетический
спектр свободной частицы непрерывен.
Плотность вероятности___________________________________________________________
М![]() ера
вероятности нахождения частицы в момент
времениt
в окрестности
данной точки пространства. В данном
случае плотность вероятности не
зависит ни от времени, ни от координат:
все положения
свободной частицы в пространстве
равновероятны.
ера
вероятности нахождения частицы в момент
времениt
в окрестности
данной точки пространства. В данном
случае плотность вероятности не
зависит ни от времени, ни от координат:
все положения
свободной частицы в пространстве
равновероятны.
6.2.8. ЧАСТИЦА В ОДНОМЕРНОЙ ПОТЕНЦИАЛЬНОЙ ЯМЕ
С БЕСКОНЕЧНО ВЫСОКИМИ СТЕНКАМИ
6.39 Потенциальная яма с бесконечно высокими стенками_________________________
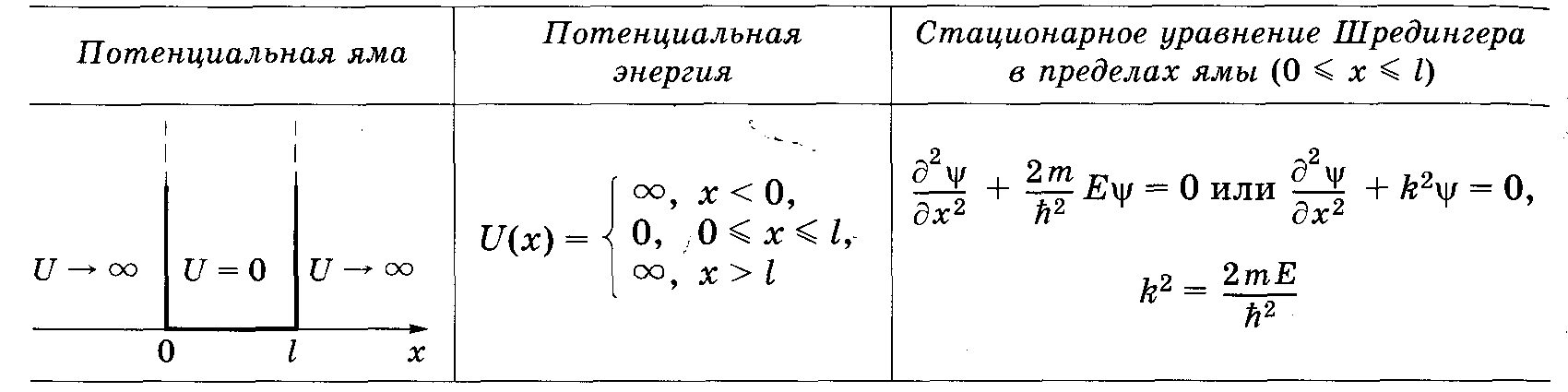
[![]() — ширина ямы; энергия отсчитывается от
дна ямы;k
—
волновое число; Е
—
полная
энергия частицы]
— ширина ямы; энергия отсчитывается от
дна ямы;k
—
волновое число; Е
—
полная
энергия частицы]
6.40 Решение уравнения Шредингера для частицы в яме_____________________________
Граничные условия_______________________________________________________________
Э![]() то
следует из условия непрерывности. За
пределы ямы
частица не
проникает, и в областях х
< 0 и х
> I
волновая
функция Ψ(х) = 0.
то
следует из условия непрерывности. За
пределы ямы
частица не
проникает, и в областях х
< 0 и х
> I
волновая
функция Ψ(х) = 0.
Общее решение уравнения Шредингера_____________________________________________
Ψ![]() (0)
= Ψ(
(0)
= Ψ(![]() )
= 0, поэтому В
= 0.
)
= 0, поэтому В
= 0.
Условию
Ψ(![]() )
= А sin
k
)
= А sin
k![]() =
0 удовлетворяет
=
0 удовлетворяет
![]()
(n = 1,2,3,...).
Собственные функции____________________________________________________________
А![]() =
=![]() (коэффициент находится из условия
нормировки:
(коэффициент находится из условия
нормировки:
![]() )
)
Нормированные собственные функции_____________________________________________
З начениеп = 0
приводит к тривиальному результату
Ψ(x)
= 0, а отрицательные значения п
— к тем же
функциям, но с отрицательным знаком,
что не дает новых физических решений.
начениеп = 0
приводит к тривиальному результату
Ψ(x)
= 0, а отрицательные значения п
— к тем же
функциям, но с отрицательным знаком,
что не дает новых физических решений.
318
