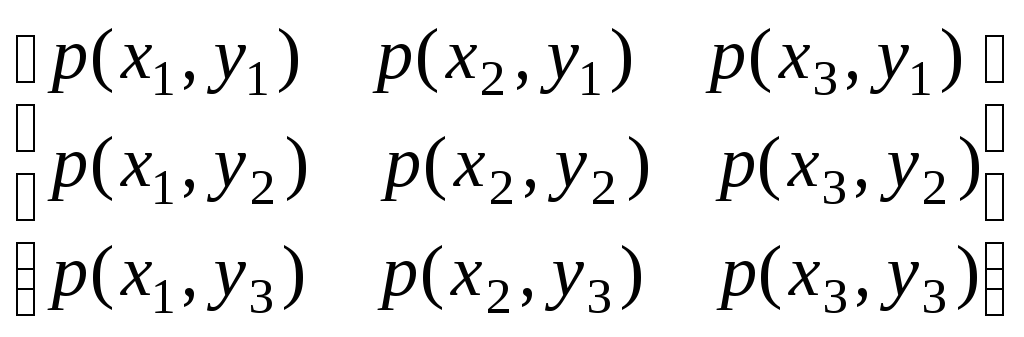3.3. Задачі
3.3.1.
Маємо трійковий стаціонарний канал без
пам’яті та без витирання. Ймовірності
p(xi, yk)
сумісного виникнення
символу xi
на вході каналу та
символу yk
– на його виході
для різних варіантів наведені у другому
стовпці таблиці 3.3.1. Знайти середню
кількість I (Y, X )
інформації, що переноситься одним
символом, швидкість
передачі інформації по каналу та
пропускну здатністьC
каналу. Чисельні значення швидкості
v0
передачі символів
по каналу ( в Бодах)
наведені у третьому
стовпці таблиці 3.3.1.
Таблиця 3.3.1
|
№ варіанта |
|
v0, Бод |
|
1 |
|
50 |
|
2 |
|
75 |
|
3 |
|
100 |
|
4 |
|
120 |
|
5 |
|
150 |
|
6 |
|
200 |
|
7 |
|
300 |
|
8 |
|
600 |
|
9 |
|
1200 |
|
10 |
|
2400 |
|
11 |
|
50 |
|
12 |
|
75 |
|
13 |
|
100 |
|
14 |
|
120 |
|
15 |
|
150 |
|
16 |
|
200 |
|
17 |
|
300 |
|
18 |
|
600 |
|
19 |
|
1200 |
|
20 |
|
2400 |
3.3.2. Розрахувати пропускну здатність C двійкового стаціонарного симетричного по входу каналу без пам’яті із витиранням. Вихідні дані, а саме, ймовірності
– правильного прийому двійкового символу q ;
– помилки при його передачі по каналу pП ;
– витирання символу pВ ,
а також швидкість v0 передачі символів по каналу ( в Бодах) для різних варіантів наведені у таблиці 3.3.2.
Таблиця 3.3.2
|
№ варіанта |
q |
pП |
pВ |
v0 |
№ варіанта |
q |
pП |
pВ |
v0 |
|
1 |
0,90 |
0,02 |
0,08 |
100 |
11 |
0,90 |
0,03 |
0,07 |
200 |
|
2 |
0,87 |
0,01 |
0,12 |
120 |
12 |
0,95 |
0,01 |
0,04 |
300 |
|
3 |
0,95 |
0,01 |
0,04 |
150 |
13 |
0,87 |
0,03 |
0,10 |
600 |
|
4 |
0,88 |
0,03 |
0,09 |
200 |
14 |
0,84 |
0,04 |
0,12 |
1200 |
|
5 |
0,83 |
0,03 |
0,14 |
300 |
15 |
0,94 |
0,01 |
0,05 |
2400 |
|
6 |
0,80 |
0,02 |
0,18 |
600 |
16 |
0,81 |
0,02 |
0,17 |
50 |
|
7 |
0,92 |
0,02 |
0,06 |
1200 |
17 |
0,88 |
0,02 |
0,10 |
75 |
|
8 |
0,80 |
0,05 |
0,15 |
2400 |
18 |
0,86 |
0,03 |
0,11 |
100 |
|
9 |
0,91 |
0,01 |
0,08 |
50 |
19 |
0,93 |
0,01 |
0,06 |
120 |
|
10 |
0,88 |
0,02 |
0,10 |
75 |
20 |
0,89 |
0,01 |
0,10 |
150 |
3.3.3. Отримати чисельні значення ймовірностей спотворення t або більшої кількості символів в кодовій комбінації двійкового коду довжиною n при передачі її через біноміальний каналу, в якому символи спотворюються із ймовірністю р, та через двійковий канал з групуванням помилок, який описується моделлю Пуртова із таким же, як і для біноміального каналу, значенням середньої ймовірності помилки при передачі двійкового символу р та із коефіцієнтом групування . Вихідні дані для різних варіантів наведені у таблиці 3.3.3.
Таблиця 3.3.3
|
№ варіанта |
n |
t |
p |
|
№ варіанта |
n |
t |
p |
|
|
1 |
15 |
1 |
310 – 3 |
0,50 |
11 |
14 |
2 |
210 – 4 |
0,80 |
|
2 |
13 |
2 |
210 – 3 |
0,55 |
12 |
12 |
3 |
10 – 4 |
0,30 |
|
3 |
11 |
3 |
10 – 3 |
0,30 |
13 |
10 |
1 |
310 – 3 |
0,35 |
|
4 |
9 |
1 |
510 – 4 |
0,35 |
14 |
8 |
1 |
510 – 3 |
0,40 |
|
5 |
7 |
2 |
10 – 2 |
0,40 |
15 |
6 |
2 |
310 – 3 |
0,45 |
|
6 |
14 |
3 |
10 – 4 |
0,45 |
16 |
15 |
3 |
10 – 4 |
0,50 |
|
7 |
12 |
1 |
310 – 4 |
0,50 |
17 |
13 |
1 |
510 – 4 |
0,55 |
|
8 |
10 |
2 |
210 – 3 |
0,55 |
18 |
11 |
2 |
310 – 4 |
0,65 |
|
9 |
8 |
2 |
10 – 2 |
0,65 |
19 |
9 |
3 |
10 – 3 |
0,75 |
|
10 |
6 |
1 |
210 – 2 |
0,75 |
20 |
7 |
1 |
210 – 3 |
0,80 |