
- •Теорія інформації та кодування
- •Передмова
- •1. Дискретні джерела інформації
- •1.1. Теоретичні положення
- •1.2. Приклади розв’язання задач Задача 1.2.1
- •1.3. Задачі
- •2. Ефективне кодування
- •2.1. Теоретичні положення
- •2.2. Приклади розв’язання задач
- •Розв’язання. Необхідною умовою побудови нерівномірного коду, що однозначно декодується, є виконання нерівності Крафта. Підставивши значення довжин кодових комбінацій у (2.1), отримаємо
- •Задача 2.2.2
- •Задача 2.2.5
- •2.3. Задачі
- •3. Дискретні канали зв’язку
- •3.1. Теоретичні положення
- •3.2. Приклади розв’язання задач Задача 3.2.1
- •Задача 3.2.2
- •Задача 3.2.3
- •Задача 3.2.4
- •Задача 3.2.5
- •Задача 3.2.7
- •Задача 3.2.8
- •Задача 3.2.9
- •Задача 3.2.10
- •3.3. Задачі
- •4. Коди, їх класифікація та основні характеристики
- •4.1. Теоретичні положення
- •4.2. Приклади розв’язання задач Задача 4.2.1
- •Задача 4.2.2
- •4.3. Задачі
- •5. Двійково-десяткові та двійкові рефлексні коди
- •5.1. Теоретичні положення
- •5.2. Приклади розв’язання задач
- •5.3. Задачі
- •6. Штрихові коди
- •6.1. Теоретичні положення
- •6.2. Приклади розв’язання задач Задача 6.2.1
- •Задача 6.2.2
- •6.3. Задачі
- •7. Двійкові коди, що виявляють помилки
- •7.1. Теоретичні положення
- •7.2. Приклади розв’язання задач Задача 7.2.1
- •Задача 7.2.3
- •Задача 7.2.4
- •7.3. Задачі
- •8. Двійкові коди, що виправляють однократні помилки
- •8.1. Теоретичні положення
- •8.2. Приклади розв’язання задач
- •8.3. Задачі
- •9. Двійкові циклічні коди
- •9.1. Теоретичні положення
- •9.2. Приклади розв’язання задач
- •9.3. Задачі
- •10. Недвійкові коди
- •10.1. Теоретичні положення
- •10.2. Приклади розв’язання задач
- •10.3. Задачі
- •11. Стиснення повідомлень при передачі даних
- •11.1. Теоретичні положення
- •11.2. Приклади розв’язання задач
- •11.3. Задачі
- •12. Канальні коди
- •12.1. Теоретичні положення
- •12.2. Приклади розв’язання задач
- •12.3. Задачі
- •Література
- •Додатки Додаток а. Двійкові логарифми цілих чисел
- •Додаток б. Таблиця значень функції – p log 2 p
- •Додаток в. Десяткові коди країн, що використовуються при штриховому кодуванні
Задача 3.2.9
Через стаціонарний несиметричний двійковий канал без пам’яті з матрицею перехідних ймовірностей
передаються кодові комбінації двійкового коду довжиною n = 5. Всі кодові комбінації однаково ймовірні. Знайти ймовірність того, що в кодовій комбінації на виході каналу
– помилки будуть відсутні;
– буде спотворено точно один двійковий символ на будь-якій позиції кодової комбінації.
Розв’язання. Ймовірність Р(0,5) відсутності спотворених символів в кодовій комбінації на виході каналу розраховується за виразом
-
 ,
,
де
P{n0 = i} = C ![]() /2 5
– ймовірність того, що в кодовій
комбінації на виході каналу буде точно
і нулів
( кількість одиниць при цьому буде
дорівнювати 5 – і );
/2 5
– ймовірність того, що в кодовій
комбінації на виході каналу буде точно
і нулів
( кількість одиниць при цьому буде
дорівнювати 5 – і );
P{s = 0 / n0 = i} – ймовірність того, що при передачі кодової комбінації, до складу якої входить точно і нулів, не буде спотворено жодного символу.
Оскільки канал не має пам’яті,
P{s = 0 / n0 = i} = p(0/0)i p(1/1)5–i.
Підставляючи в наведені вирази значення перехідних ймовірностей каналу, отримаємо
Р(0,5) = 0,753632 .
Ймовірність Р(1,5) спотворення точно одного двійкового символу можна знайти таким чином:
-
 ,
,
де P{s = 1 / n0 = i} – ймовірність того, що при передачі по каналу кодової комбінації, до складу якої входить точно і нулів, буде спотворено точно один символ.
Спотворення точно одного символу при передачі по каналу двійкової комбінації, яка має і нулів, та ( 5 – і ) одиниць, може відбутися одним із двох несумісних випадків: спотворюється тільки один із і нулів та всі ( 5 – і ) одиниць передаються безпомилково або спотворюється тільки одна із ( 5 – і ) одиниць та всі і нулів передаються безпомилково. З урахуванням цього маємо
Підставляючи перехідні ймовірності каналу, отримаємо
Р(1,5) = 0,219311.
Як бачимо, розрахунки для несиметричного каналу значно складніші, ніж для симетричного.
Задача 3.2.10
Повідомлення деякого дискретного джерела інформації передаються кодовими комбінаціями завадостійкого двійкового коду довжиною n = 31. Код здатен виправляти всі помилки кратності один, два та три. Якщо ж в кодовій комбінації буде спотворено більше трьох символів, спотворена кодова комбінація буде декодована невірно, тобто одержувач отримає не те повідомлення, яке передавалось.
Знайти ймовірність того, що повідомлення, яке передається кодовою комбінацією такого коду, буде декодовано помилково, якщо для передачі використовується
– біноміальний канал із ймовірністю спотворення двійкового символу p = 0,001;
– канал із групуванням помилок, що описується моделлю Пуртова зі значеннями параметрів р = 0,001; = 0,8 .
Розв’язання. Повідомлення буде декодоване помилково, якщо в кодовій комбінації буде спотворено чотири або більше двійкових символів. Ймовірність PП такої події
-
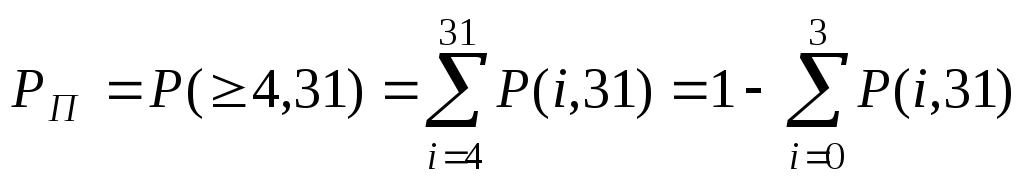 .
.
Для біноміального каналу краще користуватись останнім співвідношенням:
![]()
Для каналу із групуванням помилок маємо згідно з виразом (3.18)
Аналіз
отриманих результатів свідчить про
значну ефективність застосування
завадостійкого кодування при передачі
повідомлень через біноміальний канал
– ймовірність отримання одержувачем
помилкового повідомлення буде дуже
малою:
![]()
Щоб
зробити висновок про доцільність
використання завадостійкого кодування
при передачі повідомлень через канал
із групуванням помилок, розрахуємо
ймовірність
![]() будь-якого спотворення кодової комбінації:
будь-якого спотворення кодової комбінації:
Таку
ймовірність невірної передачі повідомлення
будемо мати без застосування будь-якого
завадостійкого коду. Оскільки ця величина
незначно відрізняється від ймовірності
![]() помилкового декодування для завадостійкого
коду, застосування завадостійкого
кодування в цьому випадку навряд чи є
доцільним.
помилкового декодування для завадостійкого
коду, застосування завадостійкого
кодування в цьому випадку навряд чи є
доцільним.
