3.2. Приклади розв’язання задач Задача 3.2.1

Знайти пропускну здатність трійкового стаціонарного каналу без пам’яті, який має таку матрицю перехідних ймовірностей

.

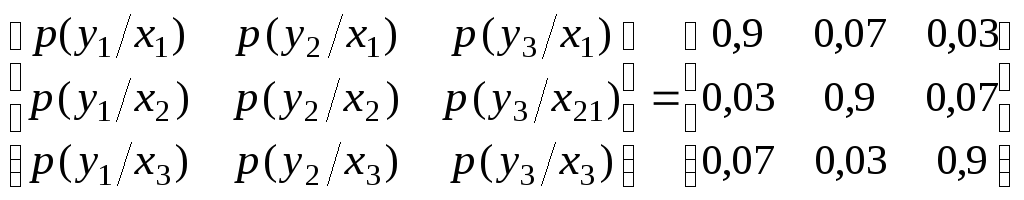Швидкість передачі символів по каналу v₀ = 100 Бод.

Знайти середню кількість інформації, що переноситься одним символом, та швидкість передачі інформації по такому каналу від дискретного немарковського джерела інформації з алфавітом X  = = {x₁, x₂, x₃}, якщо ймовірності виникнення символів

Часові характеристики джерела та каналу узгоджені, тобто тривалість кожного символу на виході джерела

Розв’язання. Аналізуючи матрицю перехідних ймовірностей ка-налу, можна зробити висновок, що канал є симетричним в посиленому значенні, тому для розрахунку пропускної здатності каналу скористуємося виразом (3.14):

Швидкість передачі інформації розрахуємо, користуючись виразом (3.8). Щоб отримати H ( Y  ), знайдемо за виразом

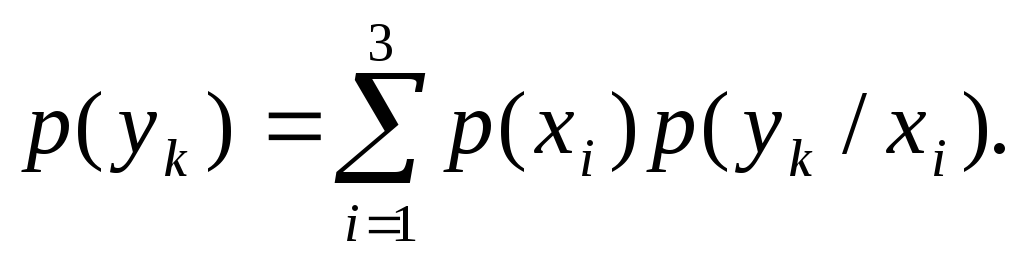
(3.19)

Маємо p( y₁) = 0,556 ; p( y₂) = 0,315 ; p( y₃) = 0,129 ;

H ( Y  )  =  1,377 біт.

Нарешті = 100  ( 1,377 – 0,557 )  =  82 біт / с .

Задача 3.2.2

Для каналу задачі 3.2.1 знайти середню кількість інформації, що переноситься одним символом, та швидкість передачі інформації по каналу, якщо до входу каналу підключене марковське стаціонарне дискретне джерело інформації задачі 1.2.6.

Розв’язання. Оскільки до входу каналу підключене марковське джерело, вихід каналу теж в загальному випадку буде являти собою марковське джерело, при цьому глибина пам’яті може бути більше одиниці. Це ускладнює застосування виразів (3.6) та (3.8), оскільки для розрахунків H (Y ) недостатньо знати тільки безумовні ймовірності p( y_k ) виникнення символів на виході каналу; треба знати також умовні ймовірності p( y_k /s), де s – стан джерела з алфавітом Y ( виходу каналу ), який визначається попередніми символами на виході каналу.

Для розрахунку середньої кількості інформації, що переноситься одним символом, доцільніше в цьому випадку користуватись виразом (3.5). Щоб знайти умовну ентропію H ( X /Y  ), треба знайти умовні ймовірності , для чого скористуємося виразом

Ймовірності p(x_i) та p( y_k /x_i) є відомими. Для розрахунку ймовірностей p(y_k) скористуємося виразом (3.19). Маємо

p(x₁) = 0,70037;  p(x₂) = 0,16802;  p(x₃) = 0,13161.

Тепер знаходимо набір ймовірностей :

.

Умовна ентропія H ( X /Y  )  =  0,4 біт.

Кількість інформації, що переноситься одним символом, з урахуванням значення ентропії H_П1( X  ), отриманого в задачі 1.2.6 :

I (Y, X ) =  1,001 – 0,4 = 0,601 біт.

Швидкість передачі інформації по каналу

=  v₀  I (Y, X )  =  100  0,601 =  60,1 біт /c .

Задача 3.2.3

Отримати вирази для пропускної здатності симетричного в посиленому значенні каналу без пам’яті для довільної потужності М алфавіту та для біноміального каналу. Проаналізувати залежність пропускної здатності біноміального каналу від ймовірності р помилки в каналі.

Розв’язання. Матриця перехідних ймовірностейдля симетричного в посиленому значенні каналу з алфавітом потужностіМ міститьМ рядків,М стовпців та має вигляд

.

(3.20)

Тут – ймовірність виникнення конкретної помилки при передачі символу по каналу ( наприклад, перехід символух₁ в символ y₃ ). Слід відрізняти цю ймовірність від ймовірності р_n виникнення будь-якої помилки, яка дорівнює

.

Оскільки канал симетричний в посиленому значенні є симетричним і в послабленому значенні, скористуємося виразом (3.14), підставивши в нього ймовірності із першого рядка матриці (3.20):

.

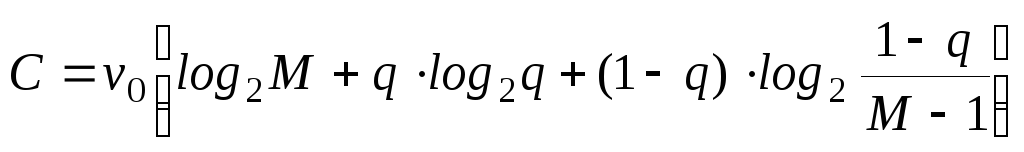(3.21)

Для біноміального каналу M = 2; 1 – q = p, тому отримаємо

.

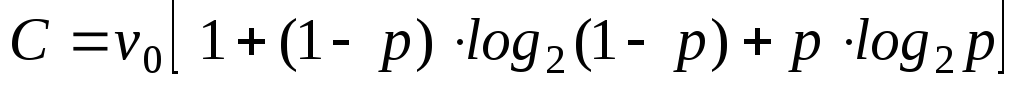(3.22)

Розраховуючи С при значеннях р в інтервалі від 0 до 1, отримаємо залежність С від р, яку зображено на рис. 3.1. Аналізуючи цю

Рис.3.1. Графік залежності пропускної здатності від ймовірності помилки для біноміального каналу

залежність, бачимо, що при p = 0 пропускна здатність C чисельно до-рівнює швидкості передачі символів. Через це іноді ці дві характеристики ототожнюють, що принципово не вірно. При збільшенні р від 0 до 0,5 пропускна здатність зменшується від до 0. При р = 0,5 пе-редача інформації неможлива. Подальше збільшення р призводить до збільшення пропускної здатності, і при р = 1 маємо С = . Очевидно, що при р = 1 всі символи при передачі в каналі будуть інвертуватися ( і це відомо на приймальній стороні! ), тому для правильного прийому повідомлень всі символи на виході каналу треба піддавати інверсії.