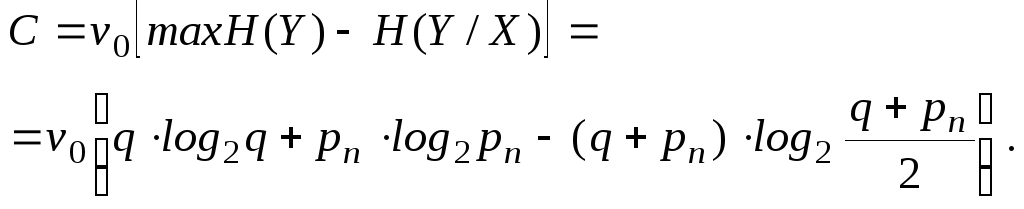- •Теорія інформації та кодування
- •Передмова
- •1. Дискретні джерела інформації
- •1.1. Теоретичні положення
- •1.2. Приклади розв’язання задач Задача 1.2.1
- •1.3. Задачі
- •2. Ефективне кодування
- •2.1. Теоретичні положення
- •2.2. Приклади розв’язання задач
- •Розв’язання. Необхідною умовою побудови нерівномірного коду, що однозначно декодується, є виконання нерівності Крафта. Підставивши значення довжин кодових комбінацій у (2.1), отримаємо
- •Задача 2.2.2
- •Задача 2.2.5
- •2.3. Задачі
- •3. Дискретні канали зв’язку
- •3.1. Теоретичні положення
- •3.2. Приклади розв’язання задач Задача 3.2.1
- •Задача 3.2.2
- •Задача 3.2.3
- •Задача 3.2.4
- •Задача 3.2.5
- •Задача 3.2.7
- •Задача 3.2.8
- •Задача 3.2.9
- •Задача 3.2.10
- •3.3. Задачі
- •4. Коди, їх класифікація та основні характеристики
- •4.1. Теоретичні положення
- •4.2. Приклади розв’язання задач Задача 4.2.1
- •Задача 4.2.2
- •4.3. Задачі
- •5. Двійково-десяткові та двійкові рефлексні коди
- •5.1. Теоретичні положення
- •5.2. Приклади розв’язання задач
- •5.3. Задачі
- •6. Штрихові коди
- •6.1. Теоретичні положення
- •6.2. Приклади розв’язання задач Задача 6.2.1
- •Задача 6.2.2
- •6.3. Задачі
- •7. Двійкові коди, що виявляють помилки
- •7.1. Теоретичні положення
- •7.2. Приклади розв’язання задач Задача 7.2.1
- •Задача 7.2.3
- •Задача 7.2.4
- •7.3. Задачі
- •8. Двійкові коди, що виправляють однократні помилки
- •8.1. Теоретичні положення
- •8.2. Приклади розв’язання задач
- •8.3. Задачі
- •9. Двійкові циклічні коди
- •9.1. Теоретичні положення
- •9.2. Приклади розв’язання задач
- •9.3. Задачі
- •10. Недвійкові коди
- •10.1. Теоретичні положення
- •10.2. Приклади розв’язання задач
- •10.3. Задачі
- •11. Стиснення повідомлень при передачі даних
- •11.1. Теоретичні положення
- •11.2. Приклади розв’язання задач
- •11.3. Задачі
- •12. Канальні коди
- •12.1. Теоретичні положення
- •12.2. Приклади розв’язання задач
- •12.3. Задачі
- •Література
- •Додатки Додаток а. Двійкові логарифми цілих чисел
- •Додаток б. Таблиця значень функції – p log 2 p
- •Додаток в. Десяткові коди країн, що використовуються при штриховому кодуванні
Задача 3.2.4
З якою
максимальною швидкістю при як завгодно
малій ймовірності спотворення повідомлень
можна передавати інформацію через
біноміальний канал, якщо технічна
швидкість передачі символів
![]() ,
а ймовірність помилки при передачі
двійкового символуp
= 0,1; р
= 0,01.
,
а ймовірність помилки при передачі
двійкового символуp
= 0,1; р
= 0,01.
Розв’язання.Для відповіді на поставлене в умовах задачі запитання треба знайти пропускну здатність каналу. Підставивши чисельні значення у вираз (3.22), маємо:
для p = 0,1
для p = 0,01
Аналізуючи отримані результати, можна зробити висновок, що при p = 0,1 із кожної тисячі двійкових символів 531 передають інформацію, а 469 ( майже половина ) використовується для боротьби із завадами. Якщо ж p = 0,01, то для захисту інформації від завад достатньо виділяти 81 символ на 1000 символів, тобто менше 10%.
Задача 3.2.5
Знайти чисельним методом пропускну здатність двійкового стаціонарного несиметричного каналу без пам’яті та без витирання, який має таку матрицю перехідних ймовірностей
-
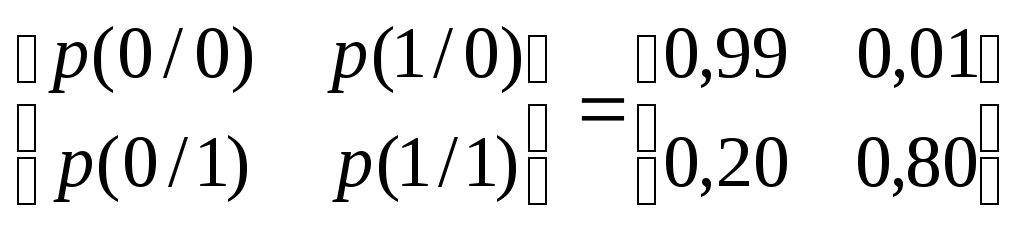 .
.
Швидкість
передачі символів
![]() .
.
Розв’язання. Будемо використовувати вираз (3.11) для пропускної здатності. З урахуванням обмежень умов задачі ентропіюН(Y) можна знайти таким чином:
Для умовної ентропії Н(Y/Х) маємо:
![]()
![]()
Підставляючи
у наведені вирази значення перехідних
ймовірностей
![]() та надаючи
та надаючи![]() різні значення, отримаємо дані, що
наведені у таблиці 3.1.
різні значення, отримаємо дані, що
наведені у таблиці 3.1.
Аналізуючи дані
таблиці 3.1, робимо висновок, що пропускна
здатність дорівнює 0,57787 біт/с
і досягається ( на відміну від симетричного
каналу ) при суттєво неоднаково ймовірних
символах на виході каналу, а саме при
![]() ;
;![]() .
Проте розподіл ймовірностей
.
Проте розподіл ймовірностей![]() появи символів на вході каналу, який
забезпечує максимальне значення
швидкості передачі інформації, незначно
відрізняється від однаково ймовірного
:
появи символів на вході каналу, який
забезпечує максимальне значення
швидкості передачі інформації, незначно
відрізняється від однаково ймовірного
:![]() ;
;![]() .
.
Таблиця 3.1
|
|
|
|
|
|
|
0,4 |
0,516 |
0,9993 |
0,4655 |
0,5338 |
|
0,45 |
0,5555 |
0,9911 |
0,4334 |
0,5577 |
|
0,5 |
0,595 |
0,9738 |
0,4014 |
0,5724 |
|
0,55 |
0,6345 |
0,94715 |
0,36930 |
0,57785 |
|
0,553 |
0,6369 |
0,94525 |
0,36738 |
0,57787 |
|
0,6 |
0,674 |
0,9108 |
0,3372 |
0,5736 |
|
0,65 |
0,7135 |
0,8642 |
0,3052 |
0,559 |
|
0,7 |
0,753 |
0,8065 |
0,2731 |
0,5334 |
Крім того, навіть
значне відхилення
![]() від 0,553 незначно знижує швидкість
передачі інформації. Якщо ж символи на
вході каналу будуть однаково ймовірними,
швидкість передачі інформації буде
відрізнятись від пропускної здатності
лише на
від 0,553 незначно знижує швидкість
передачі інформації. Якщо ж символи на
вході каналу будуть однаково ймовірними,
швидкість передачі інформації буде
відрізнятись від пропускної здатності
лише на
( 0,57787 – 0,5724 ) / 0,57787 · 100 % = 0,9466 %.
Задача 3.2.6
Визначити пропускну здатність двійкового каналу без пам’яті з витиранням, який має таку матрицю перехідних ймовірностей
-
 .
.
Розв’язання.
Канал є симетричним по входу. Це означає,
що умовна ентропія Н(Y/Х)
не залежить від
розподілу
ймовірностей
![]() появи символів на вході каналу. Для
отримання пропускної здатності в цьому
випадку можна скористатися виразом
(3.13), тобто необхідно знайти значення
появи символів на вході каналу. Для
отримання пропускної здатності в цьому
випадку можна скористатися виразом
(3.13), тобто необхідно знайти значення![]() ,
яке максимізує
,
яке максимізує![]() .
.
Отримаємо вирази
для ймовірностей
![]() появи символів на виході каналу:
появи символів на виході каналу:
Ймовірність
![]() не залежить від розподілу ймовірностей
появи символів на вході каналу, тому
для максимізації
не залежить від розподілу ймовірностей
появи символів на вході каналу, тому
для максимізації![]() необхідно, щоб різниця між
необхідно, щоб різниця між![]() та
та![]() була якомога меншою ( дивися розділ
1 ). Легко пересвідчитись, що при
була якомога меншою ( дивися розділ
1 ). Легко пересвідчитись, що при![]()
Отже