
Navch_pisib_stat+kinem
.pdf
Направлений вектор acр відповідно до напрямку вектора V у бік
увігнутості траєкторії. |
|
|
|
|
|
|
|
|
|
Прискорення точки у момент часу t |
знаходять як межу, до якої пря- |
||||||||
мує середнє прискорення aср при наближенні |
t до нуля: |
||||||||
|
|
|
|
|
|
|
|
|
|
a = lim a |
|
= lim |
V |
= |
dV |
|
|||
ср |
|
t |
dt . |
||||||
t →0 |
t→0 |
|
|
||||||
Тоді, з врахуванням (81), де V = ddtr = r& , матимемо:
|
|
|
d 2 |
r |
|
|
a = |
dV |
&& |
|
|||
dt |
= dt2 |
= r . |
(90) |
|||
Отже, вектор прискорення точки у даний момент часу дорівнює першій похідній від вектора швидкості або другій похідній від радіусавектора точки за часом.
Вектор aср лежить у площині, створеній векторами V і V1 . Коли t
прямує до нуля, точка M1 наближається до точки M , і площина векторів (V ,V1 ) повертається навколо вектора V , прагнучи до положення стичної площини. Отже вектор прискорення a лежить у стичній площині Mτn (рис.67) і направлений у бік увігнутості траєкторії.
Одиниця виміру прискорення в системі CI − 1м / c2 .
1.4.2 Визначення прискорення в декартовій системі координат
При координатному способі задавання руху прискорення точки знаходять через його проекції на координатні осі:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a = axi |
+ ay j + az k . |
(91) |
|||||
Крім того, на підставі виразу (90) з врахуванням того, що орти i, j, k незмінні, маємо
110

|
|
|
|
dV |
|
|
|
|
dVy |
|
|
|
dV |
|
|
|
|
|
|
dV |
|
x |
|
|
|
|
|
|
z |
|
|
|
|
||||
a = |
= |
i + |
|
j + |
k. |
(92) |
||||||||||||
dt |
|
|
dt |
|
|
|
||||||||||||
|
|
dt |
|
|
|
dt |
|
|||||||||||
Порівнюючи залежності (91) і (92) встановимо, що проекції вектора прискорення точки на декартові осі координат визначаються формулами:
ax = |
dVx |
= &x&; |
|
ay |
= |
|
dVy |
= &y&; |
|
az = |
dV |
z |
= &z&. |
|
|
|
(93) |
|||||||
dt |
|
|
dt |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|||||
За проекціями прискорення визначимо його модуль |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
a = |
|
ax2 + a2y + az2 |
|
|
|
|
|
|
|
(94) |
|||||||||
та направляючі косинуси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
a |
x |
|
|
|
|
|
|
|
ay |
|
|
|
|
|
|
a |
z |
|
|
|
cos(a,i ) = |
; |
cos(a, j) = |
; cos(a,k ) = |
. |
(95) |
||||||||||||||||||
|
|
|
a |
|
|
|||||||||||||||||||
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|||||
1.4.3Визначення прискорення точки при натуральному способі задавання руху
Якщо рух точки задано натуральним способом, то прискорення точки визначають через його проекції на зв’язані з рухомою точкою M натуральні осі координат: дотичну Mτ , головну нормаль Mn і бінормаль Mв (рис. 71), напрямки яких встановлені раніше в розділі 1.2.
У сусідньому положенні M1 точки натуральні осі координат змінять
свій напрямок. Кут ϕ між ортами τ |
|
і τ1 двох сусідніх дотичних осей на- |
|||||
зивається кутом суміжності. |
|
|
|
|
|
|
|
Нагадаємо деякі положення, відомі з диференціальної геометрії, які |
|||||||
стосуються властивостей кривих. Кривизною кривої в точці M називають |
|||||||
межу відношення кута суміжності до довжини елемента дуги |
s : |
||||||
K = lim |
|
ϕ |
= |
dϕ |
. |
(96) |
|
|
s |
|
|
||||
S →0 |
|
|
|
ds |
|
||
111

- |
0 |
+ |
|
||
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
t1 |
s |
|
t1 |
Dt |
|
M1 |
|
|
Dj |
|
Ds |
|
|
|
|
|
||
|
M |
t |
|
V |
t |
|
|
|
|
в
в
Рисунок 71
Радіусом кривизни кривої в точці M називається величина ρ , обер-
нена до кривизни, |
|
|
|
ρ = |
1 |
. |
(97) |
|
|||
|
k |
|
|
Подамо вектор швидкості точки, як при натуральному способі задавання руху, у вигляді
V =Vτ ×τ ,
де Vτ = s& – проекція вектора швидкості на вісь τ . Тоді, на підставі формули (90), маємо
|
|
|
|
|
|
|
d |
(V τ |
)= |
dVτ |
|
|
|
|
|
dτ |
. |
|
|
|
|||||||
a = |
dV |
|
= |
|
τ |
+ V |
|
(98) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
dt |
|
|
|
|
dt |
τ |
|
|
dt |
τ |
dt |
|
|
|
||||||||||||
Визначимо модуль і напрямок другого доданку у виразі (98): |
|
|
|||||||||||||||||||||||||
V |
dτ |
|
=V |
|
dτ |
× |
ds |
=V 2 |
dτ |
. |
|
|
(99) |
||||||||||||||
dt |
|
ds |
dt |
|
|
|
|||||||||||||||||||||
|
τ |
|
τ |
|
|
|
τ ds |
|
|
|
|
|
|
||||||||||||||
Встановимо величину і напрямок вектора |
|
dτ |
. Вектор |
τ |
|
завжди |
|||||||||||||||||||||
|
|
|
|
Ds |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|||||
направлений у бік увігнутості траєкторії і лежить в площині, що проходить
112

через точку M і вектори τ ,τ1 . Отже вектор ddsτ лежить в стичній площині,
до якої прямує площина векторів τ ,τ1 при s → 0, і направлений у бік уві-
гнутості траєкторії. Кут нахилу вектора |
dτ |
|
|
до вектора τ |
визначимо, ди- |
||||||||||||||||||||||||||||||||||||||||||
dt |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ференціюючи за s |
тотожність τ |
×τ |
=τ |
2 =1; одержимо 2 |
dτ |
|
τ |
= 0 . Із цього |
|||||||||||||||||||||||||||||||||||||||
|
ds |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
випливає, що вектори |
dτ |
|
|
і τ |
|
взаємно перпендикулярні. Отже вектор |
dτ |
|
|||||||||||||||||||||||||||||||||||||||
ds |
ds |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
направлений за головною нормаллю до центра кривизни траєкторії. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Визначаючи |
модуль |
вектора |
dτ |
, встановимо, |
що |
|
|
|
|
τ |
|
= 2sin |
|
ϕ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
(див. рис. 71). Тому |
|
|
|
|
|
|
|
|
|
|
|
ds |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Dϕ |
|
|
|
|
|
|
|
|
|
|
Dϕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
dτ |
|
= lim |
|
Dτ |
|
= lim |
|
2sin |
2 |
|
= lim |
|
|
sin 2 |
|
× Dϕ |
= lim |
|
|
Dϕ |
|
= k = |
1 |
. (100) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
ds |
|
s→0 |
|
Ds |
|
|
s→0 |
|
Ds |
|
|
s |
→0 |
|
|
|
|
Dϕ |
Ds |
|
s→0 |
Ds |
|
|
|
|
|
ρ |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Враховуючи |
встановлений |
|
напрямок |
цього |
вектора, |
|
матимемо |
|||||||||||||||||||||||||||||||||||||
|
dτ |
= |
n |
. Підставимо це значення у вираз (99), і згідно з формулою (98) |
||||||
|
ds |
|
||||||||
|
|
ρ |
|
|
|
|
|
|
||
одержимо |
|
|
|
|
|
|
||||
|
|
|
|
|
dV |
V 2 |
|
|
||
|
|
|
|
a = |
τ |
τ |
+ |
|
n , |
(101) |
|
|
|
|
|
ρ |
|||||
|
|
|
|
|
dt |
|
|
|||
|
|
|
оскільки V 2 =V 2 . З цієї формули випливає, що вектор прискорення |
|||||||
|
|
|
|
τ |
|
|
|
|
|
|
лежить у стичній площині. |
|
|
|
|
|
|
||||
|
|
|
Таким чином, вектор прискорення точки має дві складові: дотичну та |
|||||||
нормальну. Складова вектора прискорення у напрямку бінормалі дорівнює нулю, тобто aв = 0 .
Дотичне прискорення |
|
|
|
|
|
|
|
dVτ |
|
|
|
|
|
aτ = |
τ = sτ |
(102) |
||||
|
dt |
&& |
|
|
||
|
|
|
|
|
|
|
113

направлене за дотичною до траєкторії у напрямку збільшення координати s , якщо алгебраїчна швидкість точки Vτ збільшується, або в напрямку зменшення s , якщо Vτ зменшується, тобто дотичне прискорення характеризує зміну модуля швидкості точки. Проекція дотичного прискорення на вісь τ :
aτ = |
|
dVτ |
|
= s . |
|
||||
|
|
dt |
&& |
|
|||||
|
|
|
|
|
|
||||
Нормальне прискорення |
|
|
|
|
|
|
|
|
|
|
|
V |
2 |
|
&2 |
|
|||
an = |
|
|
n = |
s |
n , |
||||
ρ |
ρ |
||||||||
|
|
|
|
|
|||||
айого проекція на головну нормаль
=V 2 = s&2 an ρ n .
(103)
(104)
(105)
Це прискорення завжди направлене за нормаллю до траєкторії у напрямку увігнутості; воно характеризує зміну вектора швидкості за напрямком. Так як ці складові взаємно перпендикулярні, то модуль вектора прискорення знаходиться за формулою
|
|
|
|
|
a = a2 |
+ a2 . |
(106) |
||
|
τ |
n |
|
|
1.5 Окремі випадки руху точки
Розглянемо зведені до таблиці 1 випадки характеру руху точки в залежності від значень дотичного і нормального прискорень.
Як бачимо, тільки у випадку рівномірного прямолінійного руху точки її прискорення дорівнюють нулю. В інших окремих випадках руху точка має відмінне від нуля прискорення: при змінному прямолінійному русі прискорення точки буде тільки дотичним, при рівномірному криволінійному – тільки нормальним, а при змінному криволінійному русі прискорення точки складатиметься із дотичного і нормального прискорень.
114

Таблиця 1
Характер |
|
Значення прискорення |
|
|
Траєкторія, вектори |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
швидкості і приско- |
|||||||||||||||||||||||
руху |
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|||||||||||||||||||||||
|
aτ |
|
|
an |
|
|
|
|
рення, кінематичні за- |
|||||||||||||||||||||||||||||
точки |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
лежності |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рівномірний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
x |
||||||||
a |
= a |
|
= 0 |
an = 0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
V |
|
|
|
|
|
|
|
||||||||||||||
прямолінійний |
|
|
|
a = 0 |
|
|
|
|
|
|
|
= const; x = x0 + Vt |
||||||||||||||||||||||||||
x |
|
|
|
|
V |
|||||||||||||||||||||||||||||||||
рух |
τ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
aτ = ax = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
M a V |
|
|
|
x |
||||||||||||||||||||||
Рівнозмінний |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||||||||||||||||||||||||
= |
dV |
|
= |
|
|
an = 0 |
|
|
a = aτ |
|
|
|
|
|
|
|
V = V0 + at |
|
|
|
|
|
|
|
|
|
||||||||||||
прямолінійний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
at2 |
|
|
|
|
|
||||
|
= const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = x |
0 |
+ V t + |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
V |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рівномірний |
|
|
|
|
|
|
|
|
|
V |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n a |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
aτ = 0 |
an = |
a = an |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
криволінійний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s = s0 |
+ V t |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = const |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
aτ |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
V |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
|
|
|
V 2 |
|
0 |
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Рівнозмінний |
aτ |
= |
dt |
= |
an = |
|
ρ |
|
|
a = aτ + an |
|
|
|
|
|
|
|
V = V |
+ a t |
|
|
a |
||||||||||||||||
криволінійний |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
= const |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
τ |
a t2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s = s |
0 |
+ V |
t + |
|
τ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Треба відзначити, що дотичне прискорення дорівнює нулю, якщо точка рухається з постійною алгебраїчною швидкістю, або в моменти часу, коли алгебраїчна швидкість набуває екстремальних значень (максимум чи мінімум).
Нормальне прискорення буде дорівнювати нулю при прямолінійному русі або в місцях перегину траєкторії, тобто коли ρ = ∞ , а також в ті моменти часу, коли швидкість точки дорівнює нулю.
115

1.6Приклади визначення кінематичних характеристик руху точки
Для розв’язання задач кінематики треба знати закон руху точки, який або задають явно в умові задачі, або можна визначити із відомого руху механізму, одній із ланок якого належить розглядувана точка.
Кінематичні характеристики руху точки (швидкість, прискорення, дотичне і нормальне прискорення та ін.) визначаються за формулами (82)...(95), (101)...(106). Якщо рух задано координатним способом, тобто рівняннями (76), то швидкість і прискорення точки знаходять за формулами (83)…(85), (93)…(95). Після обчислення швидкості V і прискорення a можна знайти і дотичне та нормальне прискорення. Беручи похідну за ча-
сом від знайденого виразу V , визначаємо, що a = |
dV |
= |
Vxax + Vy ay |
. Но- |
||||
|
|
|||||||
|
|
τ |
dt |
|
|
V |
||
|
|
|
|
|
|
|||
рмальне прискорення a |
n |
знайдемо із залежності a2 |
= a2 |
+ a2 |
. Одночасно |
|||
|
|
|
|
τ |
n |
|
|
|
можна знайти радіус кривизни траєкторії ρ із формули an =V 2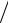 ρ .
ρ .
Якщо рух задано натуральним способом (задана траєкторія і закон руху вздовж траєкторії), то всі характеристики руху визначаються формулами (88), (93)…(95). Іноді закон руху точки траєкторією в умові задачі не наведено, і його необхідно скласти, виходячи із заданих характеру руху (рівномірний чи рівнозмінний) та значення деяких кінематичних характеристик руху в певний момент часу. Для цього застосовують формули кінематичних залежностей в окремих випадках руху точки, які наведені в таблиці 1.
Приклад 16
Знайти траєкторію точки M шатуна AB кривошипно-шатунного механізму (рис. 72), якщо довжина кривошипа OA = r = 20 см , довжина
шатуна AB = l = 20 см , відстань AM = 4l = 5 см , кут нахилу кривошипа до горизонталі змінюється за законом ϕ = 2t рад. Знайти також швидкість,
прискорення та радіус кривизни траєкторії точки в момент часу t1 = π8 сек.
116

y
A
M
B y
O ϕ
x
x
Рисунок 72
Розв’язання У даній задачі закон руху точки безпосередньо не заданий, тому в
першу чергу встановимо рівняння руху точки M у координатній формі. Для цього проведемо осі координат x та y , розмістивши їх початок
в точці O і визначимо координати точки M як функції кута ϕ . Із рисунка 72 видно, що
x = OAcosϕ + AM cosϕ = 25cosϕ ;
y = OAsinϕ − AM sinϕ =15sinϕ .
Або з врахуванням залежності кута ϕ від часу:
x = 25cos2t; y = 15sin 2t.
Для визначення рівняння траєкторії точки M виключимо час t з рівняння руху
cos2t = 25x ; sin 2t = 15y .
Піднісши обидві частини цих рівностей до квадрату та склавши їх, одержимо
117

x2 + y2 =1. 252 152
Отже, траєкторію точки M буде еліпс з півосями 25 см і 15 см з центром в точці O . Побудуємо траєкторію у вибраному масштабі і пока-
жемо на ній положення точки M у заданий момент часу t1 = π8 c , коли її координати будуть
xM |
= 25cos |
π |
=17,675 см; |
yM |
=15sin |
π |
= = 10,605 см , (рис. 73). |
|
|
4 |
|
|
|
4 |
|
Проекції вектора швидкості на осі координат
Vx = x = −50 sin 2t; |
Vy = y = 30 cos2t; |
& |
& |
модуль швидкості в будь-який момент часу:
V = 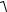
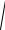 Vx2 + Vy2 =10
Vx2 + Vy2 =10
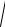 25 sin2 2t + 9 cos2 2t .
25 sin2 2t + 9 cos2 2t .
Напрямок вектора V у будь-який момент часу визначається направляючими косинусами:
æ |
|
ö |
|
Vx |
|
|
|
|
|
5 sin 2t |
|
|
|
|
||
ç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|||
cos çV , x÷ |
= |
|
|
= |
|
|
|
|
|
|
; |
|||||
|
V |
|
|
|
|
|
|
|||||||||
|
25 sin2 2t + 9 cos2 |
|
||||||||||||||
è |
|
|
ø |
|
|
|
|
|
|
2t |
||||||
æ |
|
|
ö |
|
|
Vy |
|
|
|
|
|
3 cos2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ç |
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
cos çV , y ÷ |
= |
|
V |
= |
|
|
|
25 sin2 2t + 9 cos2 |
. |
|||||||
è |
|
|
ø |
|
|
|
|
|
|
|
2t |
|||||
Прискорення точки M знайдемо за його проекціями на осі координат згідно з формулами (93) і (94):
ax = |
dVx |
= -100 cos2t; ay = -60 sin 2t; |
|
dt |
|||
|
|
118

V y
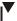











 Vy aτ
Vy aτ
ax |
Vx |
|
|
|
M |
||
|
|
||||||
|
|
|
|||||
|
|
|
|||||
|
|
|
|
|
|
|
|
0
x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ay |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
0 |
5 |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
-5 |
10 см |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
-10 |
0 |
|
10 |
20 см/с |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-10 |
0 |
|
10 |
20 см/с2 |
||||
Рисунок 73
модуль вектора прискорення
a = 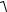
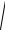 ax2 + a2y =10
ax2 + a2y =10
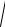 100 cos2 2t + 36 sin2 2t;
100 cos2 2t + 36 sin2 2t;
направляючі конуса вектора прискорення:
æ |
|
ö |
a |
x |
|
|
10 cos 2t |
|
|
cos ça, x÷ = |
|
= - |
|
|
|
; |
|||
|
|
|
|
|
|||||
ç |
|
÷ |
a |
100cos2 2t + 36sin 2 2t |
|
|
|||
è |
|
ø |
|
|
|||||
119
