
FOKOEP_-_CHastina_1
.pdf
|
|
y(x) g(x u) (u)du |
(109) |
|
|
Обчислимо автокореляційну функцію вихідного сигналу, що |
|
пов’язує статистичні значення вихідного сигналів y(xi ) та |
y(xk ) у |
двох точках xi та xk .
Згідно з вище наведеним визначенням,
K y (xi , xk )  y(xi ) y(xk )
y(xi ) y(xk )
|
|
|
|
|
|
|
|
|
g(xi u) (u)du g(xk ) ()d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(xi u)g(xk ) (u) ()dud |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K g (xi u)g(xk |
) (u) ()dud , |
|
|
|
|
|
|
|
|
|
|
|
|
(110) |
|
де Kg (xi |
u, xk |
) - автокореляційна функція вхідного випадкового |
|||
процесу |
g(x) . За умови, що процес стаціонарний, автокореляційна |
||||
функція |
повинна залежати тільки від |
різниці аргументів |
|||
' (x |
k |
) (x u) u u , де ' x |
k |
x , тобто |
|
|
i |
|
i |
||
|
|
|
|
|
|
K y ( ) K g ( u ) (u) ( )dud. |
(111) |
||||
|
|
|
|
|
|
Для переходу до спектра потужності стаціонарного випадкового |
|||||
процесу проінтегруємо (111) відповідно до перетворення Фур’є: |
|||||
|
|
|
|
|
|
S y (x ) K y ( ) exp(i x )d |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
K g |
( u )(u)()dud exp(i x )d , |
|
|
|
|
Змінюючи порядок інтегрування, отримаємо:
- 61 -
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S y ( x ) (u) ( )dud K g ( u ) exp(i x )d . |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
З |
|
урахуванням |
|
|
введених |
вище |
позначень, ' u , |
||||||||||||||||
перепишемо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
S y (x ) (u) exp(i xu)du K g ( ' ) exp(i x ' )d ' |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
() exp(i x )d. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
За визначенням: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
W (i x ) () exp(i x )d |
- амплітудно-фазова |
частотна |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
передаточна |
|
|
|
функція |
|
|
|
лінійної |
системи, |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
W (i x ) W * (i x ) (u) exp(i xu)du |
|
- аналогічно, |
тільки |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
комплесно спряжена величина. Відповідно: |
|
|
|
|
|
||||||||||||||||||
S |
y |
( |
x |
) |
|
W (i |
x |
) |
|
2 S |
g |
( |
x |
). |
|
|
|
|
|
|
|
|
(112) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Спектр потужності вихідного сигналу дорівнює спектру |
|||||||||||||||||||||||
потужності вхідного помноженого на |
|
W (i |
x |
) |
|
2 . |
|
||||||||||||||||
|
|
|
|||||||||||||||||||||
1.4.5. Багатовимірні випадкові процеси
Поряд з одновимірними випадковими процесами можна ввести багатовимірний випадковий процесс функції, що описує залежність від декількох аргументів:
|
|
(x1 , x2 ,..., xn ) (x) . |
(113) |
Усереднені характеристики багатовимірних випадкових процесів:
- (x) - одновимірна функція густини ймовірності
випадкового багатовимірного процесу , що характеризує густину
(x)
ймовірності в деякій точці простору із координатою x ;
- 62 -
-(xi ), ( xk ), xi , xk - двовимірна густина ймовірності, що
характеризує середньо статистичний зв’язок між імовірнісними значеннями функції одночасно у двух точках п-вимірного простору,
|
|
|
|
|
координати якого задаються радіус-векторами xi та |
xk |
; |
||
- S (x ) |
- спектр потужності |
випадкового |
багатовимірного |
|
стаціонарного процесу. |
|
|
|
|
Якщо в |
п-вимірному просторі |
статистичні |
|
характеристики |
залишаються постійними і не залежать від початку відліку в системі, |
||||
що |
|
|
|
процес буде |
визначається сукупністю координат x , то такий |
||||
стаціонарним. |
|
|
||
|
Кореляційна функція в цьому випадку виявляється залежною не |
|||
|
|
|
|
|
від самих координат xi та xk , а від розміру та напрямку вектора |
||||
|
|
|
|
|
xk |
xi . Враховуючи |
властивість ергодичності |
стаціонарного |
|
випакового процесу автокореляційна функція може бути обчислена так:
|
|
|
|
|
1 |
|
|
X1 |
X1 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
K |
|
( ) lim |
|
|
|
... |
(x ...x |
|
) |
||||||
|
|
|
|
|
|
|
|||||||||
(2)n X |
|
|
|
|
|||||||||||
|
|
X1 |
|
...X |
|
|
|
1 |
n |
(114) |
|||||
|
|
|
... |
|
|
1 |
|
n X1 X1 |
|
|
|||||
|
|
|
X n |
|
|
|
|
|
|
|
|
|
|
|
|
(x1 |
1 ,..., xn |
n )dx1...dxn . |
|
|
|
|
|
||||||||
Наприклад, стаціонарна випадкова функція (x1 , x2 ) задана |
|||||||||||||||
на площині прямокутних координат. Тоді автокореляційну функцію |
|||||||||||
можна визначити так: |
|
|
|
|
|||||||
K ( ) K (1 ,2 ) |
|
|
|
||||||||
|
|
1 |
|
|
X1 |
X 2 |
|
|
(115) |
||
lim |
|
|
|
|
(x1 x2 ) (x1 1 , x2 |
2 )dx1dx2 . |
|||||
|
|
|
|
|
|||||||
4X |
|
X |
|
|
|||||||
X1 |
|
|
|
|
|
|
|
||||
X 2 |
|
|
1 |
|
2 X1 X 2 |
|
|
|
|||
Спектральна |
|
густина |
потужності |
п-вимірного |
процесу |
||||||
|
S (x1 |
,x2 |
,...,xn ) |
|
|
|
|||||
S (x ) |
пов’язана |
з |
п-вимірною |
||||||||
автокореляційною функцією |
K ( ) парою спряжених перетворень |
||||||||||
Фур’є:
- 63 -

|
|
|
|
|
|
|
S ( x ) K ( ) exp(i x )d ; |
|
|||||
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
1 |
|
|
|
|
|
K ( ) |
|
S (x ) exp(i x )d x . |
||||
(2 )n |
||||||
|
|
|
|
|
|
|
(116)
(117)
Стаціонарні п-вимірні процеси можуть володіти властивостями ізотропності. Так, шорстка поверхня отримана методом вільного протиру. Для таких процесів автокореляційна функція залежить тільки
|
|
|
|
|
|
|
|
|||
від відстані |
між точками |
xi |
та |
xk і не залежить від напрямку самого |
||||||
|
|
|
|
|
|
|
|
|
|
|
вектора (тобто залежить від |
|
: |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
K ( |
|
|
|
|
|
|||
|
|
|
|
|||||||
(x), ( x |
) |
|
|
) . |
(118) |
|||||
У цьому випадку, якщо простір аргументів є площиною з |
||||||||||
прямокутними |
x1 , |
x2 |
чи |
|
полярними координатами , , то |
|||||
автокреляційна функція з ізотропними властивостями випадкового процесу (x1 , x2 ) буде володіти осьовою симетрією:
K (1 ,2 ) K (12 12 )1/ 2 K () .
Приклад: шорстка поверхня отримана методом вільної притирки. При цьому спектр потужності такого процесу можна знайти з перетворень Ганкеля:
|
|
|
|
S ( r ) 2 K ( )I0 ( r )d , |
(119) |
||
|
|
0 |
|
де |
|
|
|
r |
(x2 |
x2 )1/ 2 - відстань у площині зворотних |
кутових |
|
1 |
2 |
|
частот, а сама функція S (r ) також буде мати осьову симетрію.
1.4.6. Автокореляційна функція вихідного п-вимірного сигналу та його спектр потужності
Нехай на вхід лінійної п-вимірної системи, що має функцію ваги
|
|
|
|
|
(x) і |
амплітудночастотнопередаточну |
функцію |
- |
W (i x ) (п- |
вимірні) |
подається випадковий сигнал |
|
зі |
статичними |
g(x) |
||||
|
- 64 - |
|
|
|
характеристиками K g ( ) і Sg ( x ) . Тоді автокореляційна функція і
спектр потужності вихідного сигналу визначається такими рівностями, аналогічними виразам (111), (112):
K y ( ) K g
(n)
|
|
|
|
|
|
(120) |
( u |
v) (u) (v)dudv |
|||||
S |
|
|
|
) |
|
W (i |
|
)2 d |
|
S |
|
|
|
). |
(121) |
|
|
|
|
|
|
|
|||||||||
y |
( |
x |
|
x |
|
g |
( |
x |
|||||||
|
|
|
|
|
|
|
|
|
|
|
1.4.7. Оптимальна фільтрація корисних сигналів від завад
Проходження корисних сигналів через ОЕС, через окремі її елементи, як правило, завжди супроводжується завадами. Виникає задача знаходження (синтезу) таких функцій ваги (x) та амплітудо-
частотних передаточних функцій W (i x ) (як окремих елементів, так і
системи загалом), які при заданих характеристиках корисних сигналів і завад забезпечували би мінімальне спотворення сигналів. Для виконання цього завдання оптимізації в літературі найбільше поширення отримав метод синтезу оптимальних фільтрів, заснований на використанні критерію мінімуму середньоквадратичної похибки відтворення корисного сигналу.
Нехай на вхід лінійної системи надходить адитивна суміш корисного сигналу m(x) та завади n(x) , що характеризують одновимірні випадкові стаціонарні процеси з кореляційними функціями K m ( ) та Kn ( ) відповідно:
g(x) m(x) n(x). |
(122) |
Для будь-якої часткової реалізації стаціонарного випадкового |
|
процесу g(x) (вхідний сигнал) |
сигнал на виході y(x) визначається |
інтегралом згортки: |
|
|
|
y (x) g(x u) (u)du. |
(123) |
|
|
Визначимо таку функцію ваги (x) чи відповідну їй амплутудо- |
|
частотну передаточну функцію |
W (i x ) лінійної системи, яка би |
забезпечувала мінімальну середньоквадратичну похибку вимірювання
- 65 -

корисного сигналу, тобто мінімальне середньоквадратичне відхилення між корисним вхідним сигналом та можливим сумарним вихідним сигналом y(x) .
Будемо вважати, що у встановленому статичному режимі при відсутності завад система відтворює вхідну величину відповідно до
рівності |
yвст (x) m(x) . |
При цьому |
середньоквадратична |
похибка |
|||||
вимірів при наявності завад визначається виразом |
|
||||||||
|
|
1 |
|
X |
|
|
|
|
|
2 |
lim |
|
m(x) y(x) 2 dx, |
|
|
|
|||
2X |
|
|
|
||||||
|
X |
|
X |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
чи згідно (123): |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
X |
|
|
2 |
|
|
2 |
lim |
|
m(x) g(x u) (u)du |
dx. |
(124) |
||||
|
2X |
|
|||||||
|
X |
|
|
X |
|
|
|
|
|
Розкриваючи дужки та змінюючи порядок інтегрування, маємо:
|
|
|
|
1 |
|
X |
|
|
|
|
|
|
|
|
1 |
X |
|
|
2 |
|
lim |
|
|
m2 (x)dx 2 (u)du lim |
m(x)g(x u)dx |
|
|||||||||||
|
2X |
|
|
|||||||||||||||
|
|
|
X |
X |
|
|
|
|
|
|
|
X 2X |
X |
(125) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
1 |
X |
|
|
|
|
||
(u)du ( )d lim |
g(x u)g(x )dx. |
|
||||||||||||||||
2X |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
X |
|
X |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Перепишемо вираз (125), використовуючи позначення |
|
|||||||||||||||||
|
|
|
|
|
|
1 |
X |
|
|
|
|
|
|
|
|
|||
K |
|
(u) lim |
|
|
|
m(x)m(x u)dx, |
|
(126) |
||||||||||
m |
|
|
|
|
|
|||||||||||||
|
|
X 2X |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
X |
|
|
|
|
|
|
|
|||
K |
|
|
(u) lim |
|
|
|
m(x)g(x u)dx, |
|
(127) |
|||||||||
mg |
|
|
|
|
|
|
||||||||||||
|
|
X 2X |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
K |
|
( u) lim |
1 |
|
X g(x u)g(x )dx. |
(128) |
||||||||||||
g |
|
|
|
|
||||||||||||||
|
|
|
X |
2X |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
У результаті: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
Km (0) 2 (u)Kmg (u)du |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(129) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(u)du K g ( u)()d, |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- 66 -

де Km (u) |
- автокореляційна |
функція корисного |
вхідного сигналу |
|||||
(парна функція), |
|
|
|
|
|
|
||
Kmg (u) |
- |
функція |
взаємної |
кореляції корисного |
та |
суміші |
||
корисного із завадами на вході системи Kmg (u) Kmg (u) , |
|
|
||||||
Kg ( u) |
- автокореляційна |
функція адитивної суміші |
g (x) |
|||||
корисного |
сигналу та |
завад |
на |
вході системи |
(парна |
функція) |
||
Kg ( u) Kg (u ) .
Будемо вважати, що функція ваги лінійної системи оптимальна ( опт(x) ), якщо при її підстановці в рівняння (129) з невідомими статистичними характеристиками сигналів отримується мінімальне
значення середньоквадратичної похибки 2 |
. Рівняння |
для |
|
min |
|
визначення (u) можна отримати, виконавши |
варіацію (129) |
для |
довільної функції (u) , прирівнюючи ліву частину рівності до нуля. Варіаційний розрахунок показує, що необхідною і достатньою умовою
мінімуму величини 2 |
буде значення |
опт |
(u) , яке задовольняє |
||
|
|
|
|
|
|
наступному інтегральному рівняння: |
|
|
|||
|
|
|
|
|
|
|
Kmg (u) K g ( u) опт ()d, |
|
(130) |
||
|
|
|
|
|
|
|
Доведення: |
|
|
|
|
|
|
|
|
|
|
|
2 |
0 2 (u) Kmg (u)du (u) du K g ( u)()d |
|||
|
|
|
|
|
|
|
|
|
() d |
|
|
(u)du K g ( u) |
|
|
|||
|
|
|
|
|
|
|
u |
|
|
|
|
- 67 -
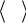
|
|
|
|
2 (u) Kmg (u)du (u) du K g ( u)()d |
|||
|
|
|
|
|
|
|
|
|
(u) du ()K g (u )d |
||
|
|
|
|
Kg (x) Kg (x) |
|
||
|
|
|
|
2 (u) Kmg (u)du 2 (u) du ( )K g ( u)d 0. |
|||
|
|
|
|
|
|
|
|
(u) Kmg (u) ( )K g |
( u)d du 0. |
||
|
|
|
|
Оскільки варіація (u) 0 , (u) - довільна функція,
Kmg ( ) опт( )K g ( u)d .
При цьому значення середньоквадратичної похибки вимірювання корисного сигналу буде таким:
опт |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
K |
m |
(0) |
|
|
опт |
(u) |
опт |
()K |
( u)dud |
|
|
|
|
|
|
п |
|
|||
|
|
|
|
|
|
|
|
|
(131) |
|
Km (0) K y (0)  m2
m2 
 y2
y2  .
.
де K y (0) - автокореляційна функція вихідного сигналу при аргументі
0 (див. (111)).
Розв’яжемо рівняння (130) частотними методами, застосувавши до його лівої та правої частин перетворення Фур’є. Отже, отримаємо:
|
|
|
|
|
|
|
|
Kmg (u) exp(i xu)du |
K g ( u) опт()d exp(i xu)du. |
||
|
|
|
|
Ліва частина цього виразу є прямим Фур’є-перетворенням від |
|||
кореляційної функції Kmg (u) , |
яка в загальному випадку - не парна |
||
функцією. Їй |
в загальному |
випадку буде відповідати спектр |
|
- 68 -

потужності Smg (i x ) . Права частина являє собою Фур’є- перетворення від згортки і дорівнює добутку Фур’є-трансформацій відповідних функцій Sg ( x ) і Wопт(i x ) , тобто
Smg (i x ) =Wопт(i x ) Sg ( x ) .
Таким чином, оптимальна амплітудо фазова частотна (АФЧ) передаточна функція лінійної системи визначається відношенням спектрів потужності корисного сигналу до сумарного сигналу.
Wопт(i x ) = Smg (i x ) / Sg ( x ) . |
|
(132) |
Знайдемо частотне представлення |
2 |
. Відповідну |
|
|
min |
оптимальну функцію ваги системи (чи оптимальну апартну функцію) можна знайти з Фур’є-перетворення:
1
опт(x) 2 Wопт(i x ) exp(i x x)d x .
Згідно з (108), (112), (131), отримуємо: |
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
K |
|
(0) K |
|
(0) |
1 |
S |
|
( |
|
) S |
|
( |
|
) d |
|
|
|||||
|
m |
y |
|
|
|
m |
x |
y |
x |
x |
|||||||||||||
|
min |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
S ( ) |
|
W |
|
(i ) |
|
2 S ( ) d . |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
m |
|
x |
|
опт x |
|
|
|
g x |
|
|
x |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
При цьому вираз |
|
|
|||
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
min 2 |
Sm |
( x ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Smg |
(i x ) |
2 |
|
|
|
|
|
|
|
||
|
|
S |
|
( |
|
) d |
|
. |
||||
|
|
|
|
|
|
y |
x |
x |
||||
|
|
( |
|
|
|
|||||||
|
S |
|
) |
|
|
|
|
|
||||
|
g |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(133)
(134)
визначає мінімальне значення середньоквадратичної похибки при вимірюваннях із допомогою оптимізованої ОЕС випадкової величини на фоні випадкових завад у спектральному представленні.
У загальному випадку, коли на вході лінійної системи сигнал m(x) чи завада n(x) взаємноскорельовані, то відповідно до визначення спектра потужності випадкового сигналу (див. 106) та виразів (127, 128), значення Smg (i x ) та Sg (x ) визначається такими сумами:
- 69 -
Sg (x ) Sm (x ) Smn (i x ) Snm (i x ) Sn (x )
Sm (x ) Sn (x ) 2RES mn (i x ), |
|
(135) |
|||||||||
Smg (i x ) Sm (x ) Smn (i x ). |
|
|
|
||||||||
Причому S |
mn |
(i |
x |
) S |
nm |
(i |
x |
) S |
(i |
x |
) . |
|
|
|
|
nm |
|
|
|||||
Доведення:
Згідно з (108) і визначенням кореляційної функції:
Kmg (u) K gm (u) , Kmn (u) Knm (u)
Kmg (u)  m(x)g(x u)
m(x)g(x u) Kmn (u)
Kmn (u)  m(x)n(x u)
m(x)n(x u)
Knm ( u)  n(x)m(x u)
n(x)m(x u)
 n(x u)m(x)
n(x u)m(x)
 m(x)n(x u)
m(x)n(x u) Kmn (u).
Kmn (u).
Smg (i x ) Kmg (u) exp(i xu)du.
|
|
Sgm (i x ) Kgm (u) exp(i xu)du u y |
|
|
|
|
|
Kgm ( y) exp(i x y)dy Kmg ( y) exp(i x y)dy,
|
|
|
|
Sgm (i x ) Sgm (i x ) Kmg ( y)exp(i x y)dy Smg (i x ).
Sgm (i x ) Smg (i x ) Smg (i x ). Smn (i x ) Snm (i x ).
Snm (i x ) Smn (i x )
Якщо завада та сигнал не скорельовані, то
Smn (i x ) Snm (i x ) 0 , і тоді:
- 70 -
