Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черновицкий национальный университет им. Ю. Федьковича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

FOKOEP_-_CHastina_2

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

1.86 Mб

Скачать

☆

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Міністерство освіти і науки України Чернівецький національний університет імені Юрія Федьковича

М.Ю. Сахновський, Ю.Я. Томка

Основи теорії перетворення оптичних сигналів

Навчальний посібник

Частина 2

Чернівці «Рута»

2007

ББК 32.86я7 С-223

УДК535.41+535.2

Друкується за ухвалою редакційно-видавничої ради Чернівецького національного університету імені Юрія Федьковича

Сахновський М.Ю., Томка Ю.Я.

С-223 Основи теорії перетворення оптичних сигналів:

Навчальний посібник. Ч. 2. – Чернівці: Рута, 2007. – 74с.

У посібнику розглядаються математичні та фізичні основи аналізу та синтезу оптико-електронних систем, найбільш характерні підходи до спектрального аналізу сигналів. Значна увага приділена дослідженню випадкових сигналів, методам їх фільтрації. Наведені методи оцінки кількості інформації, що міститься в сигналі, та у сигналі на виході системи. Розглянуті основні характеристики інформаційного поля випромінювання у просторі предметів, які формуюють вхідний сигнал для довільної оптико-електронної системи, що працює з когерентним і некогерентним випромінюванням.

Значна увага приділяється питанням флуктуації енергетичного спектра випромінювання. Отримані значення дисперсії шумів потоку випромінювання, світності та яскравості для чорних та сірих тіл.

Для студентів, які навчаються за напрямом «Оптотехніка».

ББК 32.86я7

УДК535.41+535.2

«Рута», 2007

Сахновський М.Ю., Томка Ю.Я., 2007

- 2 -

Розділ 2. ХАРАКТЕРИСТИКА ПОЛЯ ВИПРОМІНЮВАННЯ В ПРОСТОРІ ПРЕДМЕТІВ

2.1. Характеристика та параметри монохроматичного поля випромінювання

Відомо, що згідно із сучасними уявленнями, електромагнітне випромінювання володіє хвильовими та корпускулярними властивостями. Тому в залежності від розгляданої задачі доводиться користуватись хвильовими чи корпускулярними представленнями.

Хвильове представлення добре описує явища дифракції, відбивання, заломлення, що відіграє важливу роль у формуванні зображення. Корпускулярне представлення має велике значення при вивченні взаємодії випромінювання з речовиною.

Всі основні закони хвильової теорії базуються на електромагнітній теорії, основою якої є рівняння Максвелла. В диференціальній

векторній формі ці рівняння мають такий вигляд:

		B
				B H ,
rotE			,
	t
	D				(2.1)
rotH			j,	D E,
	t
divD , divB			0, j	(E Ecтр ),

де	E ,	H - вектори напруженостей електричного та магнітного полів;

D	-	вектор електричного	зміщення (індукції), B -	вектор
електромагнітної індукції,			- провідність середовища, j	- вектор

густини електричного струму,			- густина просторового заряду, Ecтр

- вектор напруженості електричного поля, що створюється сторонніми

джерелами	ЕРС,	r 0		-		абсолютна			діелектрична			постійна
середовища,	0	1		-		діелектрична постійна вакууму, r -

		4 9 109
відносна діелектрична постійна середовища,										0	4 10 7	- магнітна
										0
проникність вакууму,				1		, c		- швидкість світла.
проникність вакууму,					c2	, c	0	- швидкість світла.
		0	0		c2		0
				0

- 3 -

Виникнення (збудження) електромагнітного поля пов’язано з рухом електричних зарядів при наявності прискорення.

Якщо властивості середовища (макропарамери , ) не залежать від напруженості полей і відсутні сторонні заряди та джерела ЕРС

( Ecтр 0 , 0 ), то з

рівнянь (2.1) можна отримати хвильове

рівняння,

що пов’язує між собою значення векторів напруженостей

полів у будь-якій точці

електричного E(r , t)

та магнітного H (r ,t)

простору

радіус-вектор,

проведений

дану

точку з початку

( r

координат):

2 E ( E

E ),

t 2

(2.2)

2 H ( H

H ),

t 2

де 2

- оператор набла.

z 2

У координатному записі кожне з рівнянь (2.2) розбивається на 3

рівняння

для

відповідних

складових

проекцій

Ex , Ey , Ez чи

H x , H y , H z .

2.1.1.Плоскі та сферичні хвилі

Воптиці важливе значення має введення поняття плоскої гармонічної хвилі. Прийнято вважати хвилю плоскою, якщо нормалі до її площини (поверхні) однакових фаз хвилі в кожній точці простору паралельні між собою.

Нехай у кожній початковій площині, що збігається з фронтом

хвилі, величини E та H змінюються за гармонічним законом.


E(t) E0 exp(i 0 ) exp(i t)		із частотою 2 та в

початковий момент t 0 мають фазу 0 , фронт хвилі плоский, а

саме середовище – ізотропне та нескінченне. Тоді розв’язок хвильвого рівняння (2.2) із заданими початковими умовами можна представити в такому вигляді:

- 4 -

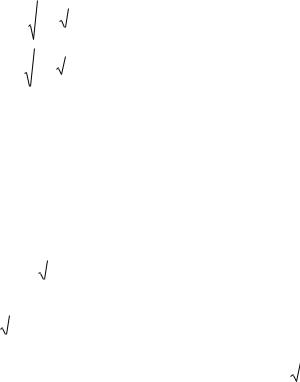
E(r , t)

E0 exp( r) exp(i 0 ) exp i( t kr ) ,

(2.3)

H (r , t)

exp(r) exp(i 0 ) exp i(t kr ) .

де -

дійсне число,

що характеризує затухання хвилі з відстанню

- радіус-

r nr ,

n - одинична нормаль до площини рівних фаз,

вектор,

проведений

із

початку координат,

де

задані

початкові

значення E0

та

у розгляданій точці

поля, k

хвильвий

k ,

вектор, що чисельно дорівнює

r -

відстань

від

початку

та k

координат до

поверхні

рівних

фаз. Значення величин

отримуються так:

cos ,

2 2

sin ,

2 2

arctg

Втрати зумовлені вихровими струмами у провідниках.

Для

поглинаючого

середовища

(провідники,

напівпровідники).

Значення затухання

виявляється таким, що не

дорівнює нулю. Якщо середовище є ідеальним діелектриком ( 0 ),

то , cos 2 0 , sin 2 1 та хвильове число

						2	2
	k					2	2		,					(2.4)
	k								,					(2.4)
				c		c
c	1	-	швидкість світла					в середовищі		в напрямку				хвильової




нормалі,			- довжина хвилі в середовищі, c0								1		- швидкість


											0	0
											0

світла у		вакуумі,			0 c0 ,				c0 / c n 0	/ ,	n -			коефіцієнт

- 5 -


заломлення	середовища, n			r . Для		поглинаючих			середовищ
c2 / c2 i		4	. Швидкість	світла	c	і	коефіцієнт		заломлення

0

виявляються		комплексними величинами.					Тому	c0 / c n i -
							0 K	K - бугерівський
комплексний коефіцієнт заломлення, а							4 ,

показник поглаинання, K / 2.

В	ізотропному нескінченному діелектричному
рівняння (2.3) набуває вигляду:
					2
E(r ,t) E0			exp( i 0 ) exp(i 0 ) exp i( t				nr ) ,
E(r ,t) E0			exp( i 0 ) exp(i 0 ) exp i( t				nr ) ,

						2
H (r ,t)		H	0 exp( i 0 ) exp(i	0 ) exp i( t				nr ) .
H (r ,t)		H	0 exp( i 0 ) exp(i	0 ) exp i( t				nr ) .

середовищі

(2.5)

Вираз (2.5) являє собою плоску гармонічну лінійно поляризовану

хвилю, оскільки електричні вектори E, H зберігають свою орієнтацію у просторі, тому що розміщені в одній площині.

Рис. 32. Плоска гармонійна лінійно поляризована хвиля

Поряд із таким представленням використовується представлення

плоскої хвилі з еліптичною поляризацією. Побачимо що, якщо є дві
		та 02
лінійно поляризовані хвилі з k	та r , із фазами 01	та 02	і різницею

- 6 -

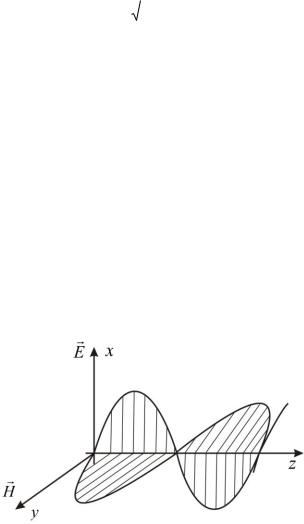
фаз 0	01 02 n			( n 0,1,2,... ), то		сумарний	електричний

вектор	E(r ,t)	E1 (r1	,t) E2 (r2		,t) буде	обертатися	в площині

(паралельно площині однакових фаз). Кінець електричного вектора в загальному випадку буде описувати еліпс.

Рис. 33

У залежності від різниці фаз обертання може відбуватись по

правому чи	лівому кругу, якщо дивитись у бік поширення хвилі

(вектора k та n ). Слід звернути увагу на те, що реальний пучок може

складатись із множини лінійно (чи еліптично) поляризованих пучків, постійна поляризації яких розподілена випадко. Тому звичайні джерела дають майже не поляризоване випромінювання.

Об’ємна густина енергії електромагнітної хвилі складається з двох

складових та розраховується згідно з формулою
W		E 2		H 2	.				(2.6)
W		2		2	.				(2.6)
		2		2
Значення W можна виразити через напруженість електричного чи

магнітного поля хвилі, оскільки вектори E та									H в діелектричному
середовищі пов’язані між собою відомими співвідношеннями
						,
E		/ l		H		,


	E						z0		(2.7)
	E		/ z						(2.7)
								,


	H						n
						- 7 -
						- 7 -

де z - хвильовий опір середовища, n -

коефіцієнт

заломлення

середовища,

z0 - хвильовий опір вакууму.

Значення

густини W ,

відповідно до (2.7), запишеться так:

/ c

чи

W E 2

H 2 .

(2.8)

Важливою характеристикою плоскої гармонічної хвилі є значення

середньої потужності, що припадає на один квадратний метр,

розташований перпендикулярно до вектора n площадки. У фотометрії ця величина називається нормальною опроміненістю.

Потужність опромінення, що проходить через площадку 1м2 , яка

розташована перпендикулярно до нормалі

n , визначається вектором

Умова-Пойтінга:

E H ,

(2.9)

де

P(t).

Для

виконання

розрахунків

потоку

Ф , що

випромінюється

об’єктом , корисно пам’ятати такі співвідношення:

W (x, y, z)d Ф ,

divP,

W (x, y, z)d divPd Pd .

(2.9а)

- поверхня, що обмежує об’єм .

У зафіксований момент часу

t * модуль вектора Умова-Пойтінга

по гармонічному

P плоскоїхвилі буде змінюватись вздовж вектора r

закону (рис. 3.4):

E 2 cos2 ( t* kr

(2.10)

Середня потужність випромінювання (нормальна опроміненість),

яка проходить через 1м2 площадки визначається усередненням (2.10) за часом:

- 8 -

		1	T 1	E 2 cos2				E 2
P	lim				( t kr		)dt	0	.
P	lim				( t kr		)dt		.
	T T		z 0			0		2z
	T T		z 0			0		2z
			0

У тому випадку, коли гармонічне електромагнітне поле створюється одним точковим джерелом (наприклад, диполь, атом і т.д.) в однорідному, ізотропному та нескінченно протяжному середовищі, то розв’язок хвильвого рівняння для довільної точки простору (окрім околу r 0 ), яка знаходиться на відстані r від джерела, має вигляд:

Рис. 34

E(r ,t)

exp( r) exp(i 0 ) exp i( t

) ,

(2.11)

H (r ,t)

exp( r) exp(i

0 ) exp i( t

) .

де E0 , H 0 - вектора напруженостей електричних і магнітних полів у початковій точці джерела, 0 - початкова фаза гармонічного процесу.

Для діелектричного середовища затухання 0 , зменшення

амплітуд E0 та H 0 відбувається обернено пропорційно радіусу r від

джерела.

Миттєве значення вектора Умова-Пойтінга вздоавж радіус-вектора

змінюється за законом:				( t 2r ).		(2.12)
	P	1	E 2 cos2	( t 2r ).		(2.12)
			0		0
		r 2 k 2 z	0		0
		r 2 k 2 z
Отже, в середовищі без втрат середня потужність
випромінювання, що проходить через 1м2						площадки від точкового
джерела, буде:

- 9 -

(2.13)

r 2 k 2 z

Весь потік, що охоплює сферу радіусом r , знаходиться так:

(2.14)

4 r 2 P

2E0 .

k 2 z

Середня потужність (потік), що припадає на одиницю тілесного

кута, тобто сила світла такого джерела, розраховується так:

E02

(2.15)

2k 2 z

2.1.2. Інтреференція монохроматичних хвиль однакової частоти

Нехай у деяку точку приходять дві хвилі від двох монохроматичних джерел із частотою ω і однаковим станом поляризації, коли електричний вектор у кожному з пучків перпендикулярний площині, в якій лежать хвильові вектора цих пучків. Зазначимо, що компланарне розміщення електричних векторів відносно площини приведе до зниження чіткості інтерференційної картини, в якій при збільшенні кута збіжності пучків збільшується

постійна складова інтенсивності.
											комплексними
Позначимо значення полів у розгляданій точці r											комплексними
функціями напруженості:

E1 (r ,t) E01 exp(i 01) exp( ik1r ) exp(i t),											(2.16)
											(2.16)
E	2	(r ,t) E		02	exp(i	02	) exp( ik		2	r ) exp(i t).
	2			02		02			2
де E01 ,			E02 -	амплітудне				значення полів від відповідних джерел,

узагальнені для випадку сферичних і плоских хвиль. Інтенсивність у

довільній точці, що задається радіус-вектором r , визначиться так (із точністю до постійного множника):

- 10 -

1 / 81 2 3 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.08.2019230.12 Кб26fitopatologiya.docx
#
14.09.2019281.86 Кб6Fizika(1).docx
#
08.11.2018285.18 Кб19fizika7_9.doc
#
28.09.201974.75 Кб3Fizyka_mag.doc
#
23.02.20161.88 Mб7FOKOEP_-_CHastina_1.pdf
#
23.02.20161.86 Mб8FOKOEP_-_CHastina_2.pdf
#
22.11.2019462.55 Кб3Fondovy_rinok_metodichka (1).docx
#
02.09.20191.13 Mб34Fotocon_SC.doc
#
23.02.2016468.01 Кб14Fotogrammetriya моє.rtf
#
23.02.201656.32 Кб29FOTOMETRIYa2014.doc
#
22.11.2019122.88 Кб3FR4_so.doc