
FOKOEP_-_CHastina_2
.pdf
2.2.3. Інтегральні перетворення когерентних полів
Як ми бачили, введення середньої частоти 0 , навколо якої відбувається коливання квазімонохроматичного хвильового процесу з
напівшириною спектра ( |
1), дозволяє схарактеризувати |
|
|
|
0 |
такий процес середньою комплексною амплітудою: |
||
|
|
|
E (r ) |
Ek (r ) E0 (x, y, z) exp(i (x, y, z)), |
|
|
|
|
E (r , t) |
Ek (r ) exp(i 0t). |
|
Середнє значення комплексної амплітуди плоскої квазімонохроматичної хвилі у прямокутній системі координат, відповідно до виразу (2.45), можна визначити рівнянням
|
|
|
|
|
|
|
|
0, t) |
2 |
1/ 2 |
|
|
|
|
E (r , t) |
E |
(r |
|
|
|
|||
E (r ) |
|
|
|
|
|
|
|
|
, |
||
|
|
|
|
|
E (r |
0, t) |
|
|
|
||
|
|
0, t) |
2 |
1/ 2 |
|
|
|
|
|
|
|
де |
E (r |
|
- |
амплітуда |
плоскої хвилі, а відношення |
||||||
|
|
|
|
E (r , t) |
|||
|
0, t) |
визначає зміну фази для відстані r |
від початку |
E (r |
|
|
|
координат.
Уведення усередненої комплексної амплітуди дозволяє скористатись для опису квазімонохроматичних хвиль та інтегральних перетворень когерентних полів представленням монохроматичних
хвиль для частоти 0 , які були розглянуті вище.
Нехай у площині x0 , y0 , z0 0 набір плоских хвиль із сукупністю
хвильових векторів k створює деяке поле з комплексною амплітудою
 E (x0 , y0 , z 0)
E (x0 , y0 , z 0) .
.
- 31 -
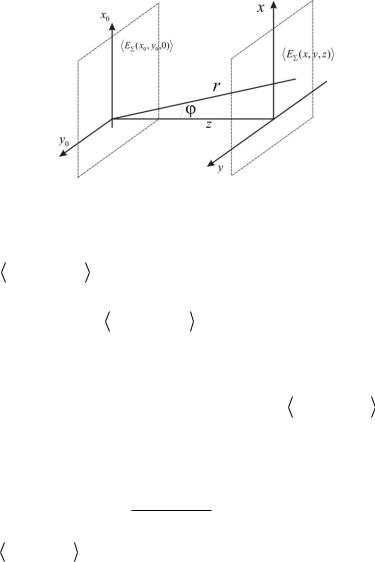
Рис. 45
Для |
поля |
у |
площині |
|
z 0 |
будуть справедливі інтегральні |
||||||||||||
перетворення |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E (x0 , y0 ,0) |
E0 ( f x , f y ) exp(i2 ( f x x f y y)df x df y , (2.45а) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
E0 ( f x , f y ) |
|
E (x0 , y0 ,0) |
exp(i2 ( f x x f y y))dxdy , |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
де f |
|
|
k |
x |
|
cos |
, |
f |
|
|
|
k y |
|
cos |
, |
|||
x |
|
|
|
|
y |
|
|
|
|
|||||||||
|
|
2 |
0 |
|
|
|
|
|
2 |
|
|
0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
функція E0 ( fx , f y ) |
є кутовим спектром поля E (x0 , y0 ,0) . |
|||||||||||||||||
Поле у площині |
x, y, z |
може бути визначене через інтегральні |
||||||||||||||||
перетворення функції E0 ( fx , f y ) |
з урахуванням амплітудночастотної |
|||||||||||||||||
фазової передаточної функції вільного простору (відстань між площинами (x0 , y0 ,0) і (x, y, z) ).
W (if x , if y ) exp(iz 
 k 2 kx2 ky2 ) .
k 2 kx2 ky2 ) .
E (x, y, z) |
|
|
|
|
(2.45б) |
E0 ( f x , f y ) exp(i2 ( f x x |
f y y))W (if x , if y )df x df y |
|
- 32 -

Згідно з теорією сигналів, будемо вважати, що на вході лінійної системи заданий вхідний сигнал  E (x0 , y0 ,0)
E (x0 , y0 ,0) , який передається через вільний простір (відстань Oz), формуючи на виході системи у
, який передається через вільний простір (відстань Oz), формуючи на виході системи у
площині |
x, y, z сигнал E (x, y, z) . |
Тоді, увівши функцію ваги |
вільного |
простору (x x0 , y y0 ) , |
вихідний сигнал можна |
визначити через двовимірну згортку: |
|
|
 E (x, y, z)
E (x, y, z)
 E (x0 , y0 ,0)
E (x0 , y0 ,0) w(x x0 , y y0 )dx0 dy0 . (2.45в)
w(x x0 , y y0 )dx0 dy0 . (2.45в)
У заданому випадку функція ваги характеризує відгук системи на монохроматичне точкове збурення поля в околі елемента площею
dx0 dy0 . Таке збурення, що передається через вільний простір, може бути визначене на основі явища дифракції. Тому, згідно із хвильовою
оптикою, функція |
(x x0 , y y0 ) повинна визначитись |
множником, який використовується при розрахунках комплексної амплітуди дифрагованої хвилі на заданому отворі й описуватиметься виразом:
(x x |
, y y |
) (i r) 1 exp(ikr) cos , |
(2.45г) |
0 |
0 |
|
|
r 
 (x x0 )2 ( y y0 )2 z2 , cos rz .
(x x0 )2 ( y y0 )2 z2 , cos rz .
У даному випадку функція (x x0 , y y0 ) має назву функції
Френеля-Кіргофа-Зоммерфельда.
Характерно, що її аналітичний вигляд можна отримати не з теорії дифракції, а використавши формалізм теорії сигналів, знаючи, що функція ваги визначається як Фур’є-перетворення від амплітудночастотної фазової передаточної функції (додаток №1).
|
|
|
|
|
|
(2.45д) |
(x, y) exp(iz k |
2 |
2 |
2 |
) exp[ i2 ( f x x f y y)]df x df y . |
||
|
kx |
ky |
|
|||
Неплоска квазімонохроматична хвиля в початковій площині z 0 може бути задана або функцією  E (x0 , y0 ,0)
E (x0 , y0 ,0) , що визначає середнє
, що визначає середнє
значення комплексних амплітуд у будь-якій точці цього простору, або кутовим спектром середніх амплітуд плоских квазімонохроматичних
- 33 -

хвиль, що описуються функціями  E (kx , ky )
E (kx , ky ) , або функціями
, або функціями
 E ( f x , f y )
E ( f x , f y ) , які в цілому утворюють неплоску хвилю на середній
, які в цілому утворюють неплоску хвилю на середній
частоті 0 2 0 2c .0
2.3. Характеристики та параметри некогерентного поля випромінювання
Для монохроматичного та когерентного випромінювання, коли простір предметів являє собою деяку площину x, y , z = 0, то
основними його характеристиками є функції розподілу комплексних амплітуд E(x, y,0) та кутовий спектр E(kx , ky ) (чи просторово-
частотний спектр E( f x , f y ) ). Повна інформація про такий спектр міститься як в амплітуді E0 , так і у фазі електромагнітного
випромінювання. Для некогерентного випромінювання, на відміну від вищевикладеного, характеристики поля будуть описуватись не комплексними функціями, що включають у себе амплітуду та фазу, а дійсними функціями, які несуть інформацію про усереднені енергетичні характеристики об’єкта, узагальнені терміном інтенсивності.
Кожна спектральна складова некогерентного випромінювання в площині x, y характеризується функцією розподілу інтенсивності
I (x, y) |
|
E |
0 |
(x, y) |
|
2 . |
(2.46) |
|
|
Рис. 46. Сила світла площадки S
- 34 -
Водночас практичні розрахунки некогерентного випромінювання проводяться з допомогою фотометричних величин і відповідним їм одиницям.
Точкові чи малорозмірні об’єкти в порівняння із відстанню до них характеризуються силою світла (рис. 46)
I |
dФ |
, |
(2.47) |
|
d |
||||
|
|
|
де dФ - елементарний потік у тілесному куті d , Ф - одиниця – вт.
1cp .
Протяжне джерело характеризується яскравістю, що являє собою потужність випромінювання з площадки dS одиничної площини, що випромінює під кутом до її нормалі в тілесний кут d , який дорівнює 1ср.
L |
dI |
|
d 2Ф |
|
|
|
|
. |
(2.48) |
||
dS cos |
d dS cos |
||||
Одиниця вимірювання яскравості - Вт см 2 |
ср 1. |
||||
Яскравість у загальному випадку визначається функцією кутів і, L L( , ) ( - полярний, - азимутальний кути).
Повна потужність потоку випромінювання, що посилається одиничною площадкою в усю верхню на півсферу, називається світністю протяжного джерела та визначається інтегралом:
2 |
/ |
2 |
|
M d L( , ) cos sin d . |
(2.49) |
||
0 |
0 |
|
|
Одиниця вимірювання - Вт см 2 .
У випадках, коли яскравість об’єкта в усіх напрямках однакова, ( L( ,) const L0 ), будемо мати:
M L0 . |
(2.50) |
Такий випромінювач (чи розсіювач) називається ламбертівським. У загальному випадку, коли протяжне джерело випромінювання
являє собою площину x, y і його спектральний склад залежить від
координат і часу, то основною характеристикою випромінювання простору предметів буде функція яскравості
- 35 -
LL(x, y, , , ,t) L(q),
залежна від шести сукупних параметрів, що характеризують розподіл яскравості по поверхні x, y , спектральний склад ( ),
напрямок ( , ) та зміни в часі (t). Цій функції можна поставити у
відповідність шестивимірний спектр Фур’є:
|
|
|
|
|
|
||
|
L(i q ) |
L(q) exp(i q q)dq, |
|||||
|
|
|
|
|
|
|
|
|
|
|
(n 6) |
|
|
|
|
x |
, y , , , ,t - сукупність |
||||||
q |
|||||||
змінних |
у |
просторі |
частот, |
|
|||
dq |
|||||||
(2.51)
відповідних незалежних - елементарний об’єм
використовуваного шестивимірного простору. |
|
|
dxdyd d d dt . |
dq |
|
Якщо відома функція L(i q ) , то зворотне Фур’є-перетворення визначає яскравість у заданому шестивимірному просторі.
|
1 |
|
|
|
|
|
|
|
L(q) |
|
|
L(i q ) exp(i q q)d q |
, |
(2.52) |
|||
(2 )6 |
||||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(n 6) |
|
|
|
|
||
Якщо оптико-електронний пристрій працює при всіх можливих реалізаціях розподілу яскравості, що змінюється за всіма незалежними змінними, а саме поле є випадковим. Для однотипних умов експерименту, для оцінки мікроструктури яскравісного поля
необхідно |
знати |
двовимірну функцію |
густини |
ймовірності |
|||
|
|
|
|
для кожної пари |
|
|
|
L(qi ), L(qk |
),qi |
, qk |
точок qi |
та qk |
у |
||
використовуваному багатовимірному просторі.
Для кожної пари таких точок можна знайти кореляційну функцію, що характеризує середньостатистичний зв’язок між значеннями яскравості в даних точках,
|
|
|
|
|
|
|
|
|
|
) |
|
dLi dLk . (2.53) |
|||||||
K L (qi |
, qk |
L(qi )L(qk |
) L(qi ), L(qk |
), qi |
, qk |
||||
(n 6)
У випадку, коли поле яскравості в усіх можливих реалізаціях за всіма незалежними змінними є стаціонарним, то кореляційна функція
|
|
|
|
стає залежною тільки від вектора різниці p qi |
qk |
довільної пари |
|
- 36 - |
|
|
|
точок багатовимірного простору, врахування властивостей ергодичності значення кореляційної функції можна визначити з розрахунку інтегралу
|
|
|
1 |
K L |
( p) lim |
|
|
|
|||
|
|
Q (2)n 6 XY A T |
|
Q |
|
|
|
|
|
|
|||
L(q)L(q |
p)dq. |
(2.54) |
||
Q
(n 6)
де - сукупність інтервалів інтегрування, що
прямують до нескінченності за всіма незалежними змінними. Якщо стаціонарне яскравісне поле описується кореляційною функцією (2.54), то для нього можна знайти спектральну густину потужності флуктуацій за всіма змінними:
|
|
|
|
|
|
|
|
|
|
SL (q ) |
K L ( p) exp(i q p)dp, |
|
(2.55) |
||||
|
|
|
|
|
|
|
|
|
|
|
(n 6) |
|
|
|
|
|
|
x , y , , , ,t |
|
|
|
|
||||
q |
- сукупність |
відповідних |
змінних у |
|||||
|
|
|
|
|
|
|
|
|
просторі частот, dp - елементарний об’єм багатовимірного простору. |
||||||||
|
Зворотне |
спряжене |
перетворення Фур’є дозволяє |
перейти від |
||||
|
|
|
|
|
|
|
|
|
спектра потужності SL (q ) до відповідної кореляційної функції. |
||||||||
|
|
1 |
|
|
|
|
|
|
|
K L ( p) |
|
|
SL (q ) exp(i q p)d q . |
(2.56) |
|||
|
(2 )n 6 |
|||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(n 6) |
|
|
|
|
|
Для більшості практичних задач можна вважати, що випромінювання в площині предметів підпорядковується закону Ламберта, при цьому важливо мати усереднену інформацію за достатньо великий проміжок часу спостереження Т про інтегральне випромінювання в деякому спектральному діапазоні . У такому випадку яскравісне поле описується тільки функцією від двох координат L L(x, y) .
У випадку, коли поле L(x, y) детерміноване (тобто має
детерміновану структуру), то воно повинно мати характерний просторово-частотний спектр.
|
|
L(i x ,i y ) L(x, y) exp i( x x y y) dxdy. |
(2.57) |
- 37 -
Зворотне Фур’є-перетворення дає значення яскравості:
|
|
|
|
L(x, y) |
1 |
|
L(i x , i y ) exp i(x x y y) d x d y . (2.58) |
4 |
2 |
||
|
|
|
|
Коли яскравість у просторі предметів розподілена випадково, то основною характеристикою такого поля буде кореляційна функція. Відомо, що для знаходження кореляційної функції в загальному
випадку необхідно |
знати |
функцію |
густини |
ймовірності |
L(xi , yi ), L(xk , yk ), xi , yi , xk , yk |
, яка |
встановлює |
середньо- |
|
статистичний зв’язок |
між яскравістю у |
двох точках площини |
||
предметів з координатами xi , yi та xk , yk .
Для стаціонарних полів двовимірна густина ймовірності залежить тільки від різниці координат і не залежить від початку відліку самих
координат та представляється у вигляді |
|
||||||||
L(x, y), L(x , yk |
), , . |
(2.59) |
|||||||
Кореляційна функція такого яскравісного поля, враховуючи |
|||||||||
властивість ергодичності, визначиться виразом |
|
||||||||
|
|
|
|
1 |
|
X Y |
|
|
|
KL ( , ) lim |
|
|
|
|
L(x, y)L(x , y )dxdy. |
(2.60) |
|||
|
|
|
|
||||||
|
|
|
|
||||||
|
X 4XY |
|
|
|
|||||
|
Y |
|
X Y |
|
|
||||
Спектральна густина потужності флуктуацій яскравості такого |
|||||||||
поля визначиться виразом |
|
|
|
||||||
|
|
|
|
|
|
|
|
||
SL (x , y ) KL ( , ) exp i(x y) d d. |
(2.61) |
||||||||
|
|
|
|
|
|
|
|||
При цьому зворотне Фур’є-перетворення визначить кореляційну |
|||||||||
функцію яскравісного поля. |
|
|
|||||||
1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
(2.62) |
|||
|
|
|
|
|
|
|
|
||
KL ( , ) (2 )2 SL ( x , y ) exp i( x y ) d x d y . |
|||||||||
|
|||||||||
|
|
|
|
|
|
|
|
|
|
У випадку коли, |
яскравісне поле L(x, y) буде випадковим та |
||||||||
ізотропним, то його просторово-частотний спектр потужності флуктуацій яскравості SL ( r ) й кореляційна функція KL ( ) визначаються парою перетворень Ганкеля.
- 38 -
|
|
SL ( r ) 2 KL ( ) I0 ( r )d . |
(2.63а) |
0 |
|
|
|
KL ( ) SL (r ) r I0 (i r )d r . |
(2.63б) |
0 |
|
де - радіус, r - частота в просторі кругових радіусів.
2.4. Характеристики яскравісного поля випромінювання в одиницях потоку квантів
Згідно з визначенням яскравість випромінювання являє собою потужність випромінювання з одиничної площадки у вигляді проекцій її площини на заданий напрямок, і відношення до одиничного тілесного кута, що охоплює заданий напрямок.
Енергетична одиниця яскравості - Вт см 2 ср 1.
Врахуємо, що, відповідно до сучасних уявлень електромагнітне випромінювання являє собою хвильовий процес, але водночас є потоком квантів енергії – фотонів. Причому випромінювання фотонів у часі має випадковий характер. До чого приведе випадковий характер випромінювання розглянемо нижче.
З погляду фотонного механізму, потужність випромінювання можна визначити кількістю фотонів, що проходять за 1с через задану площадку (чи випромінюються даною площадкою).
Нехай величина dE 1 E d характеризує енергію, отриману
тілом (чи пройдену через площадку) за час в інтервалі частот d , центрованому в околі , E - спектральна густина енергії. Цю ж
величину можна подати кількістю N ' d фотонів, що випускаються тілом за цей же час в інтервалі частот d : E d N ' d h , де
N ' - спектральна густина фотонів, визначена за час і центрована
навколо частоти , h - постіна Планка. Тоді величина |
dE 1 |
Ф d |
|
||
|
|
|
|
|
-поток випромінювання, що, за визначенням, залежить від інтервалу
і припадає на інтервал частот d . Відповідно можна записати:
-39 -
dФ( , t) Ф( , t)d |
N ' |
d h N ( , t)d h , |
|
|
|
(2.64) |
|||
|
||||
|
|
|
||
N ( ,t) - спектральна густина кількості фотонів |
в одиничному |
|||
інтервалі частот (центрованому навколо частоти ), що
випромінюються в одиницю часу при усереднені за час , Ф( ,t) |
- |
||||||||||||||||
спектральна густина |
потоку, |
dФ( ,t) |
- елементарний потік |
в |
|||||||||||||
інтервалі частот d . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Інше подання «миттєвого» світлового потоку: |
|
|
|
|
|
|
|||||||||||
dФ( , t) Ф( , t)d |
N ( , t) |
h , де |
N ( ,t) - кількість фотонів |
||||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
із частотою , |
що попали на площадку S за інтервал часу t |
|
1 |
|
у |
||||||||||||
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
момент |
t t |
t |
|
1 |
. |
Тобто |
|
миттєвий потік |
у |
спектральному |
|||||||
|
|
|
|||||||||||||||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
інтервалі |
d |
можна |
розглядати |
|
як усереднений |
за |
час t |
1 |
. |
||||||||
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, що |
t T |
, T |
|
- |
період коливань на частоті . |
|
Для |
||||||||||
|
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
560нм , T |
1,67 10 15 c. |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Якщо використати δ-функцію, то миттєвий потік, зумовлений одним фотоном можна записати в такому вигляді:
dФ1 (1, t) Ф1 ( , t)d h (t tk ),
tk - момент випромінювання або попадання фотона на площадку S . При такому підході «миттєвий» потік
N
dФ( ,t) Ф( ,t)d h (t tk ),
k 1
визначається кількістю випромінювальних N фотонів за час τ, центрованих відносно tk . Зауважимо, що при використанні δ-функції із часовою залежністю розмірність потоку – дж/с.
- 40 -
