FOKOEP_-_CHastina_2
.pdf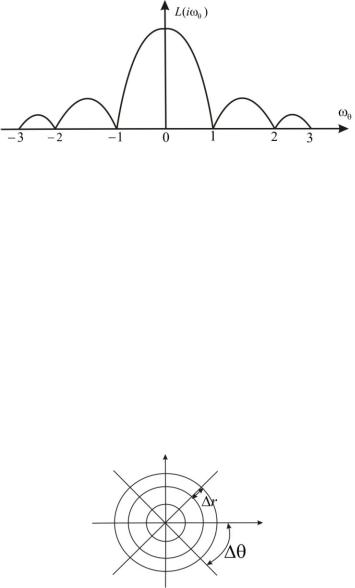
Рис. 54. Спектр функції L( )
Нулі спектра знаходяться в точках n , ( n 1,2,3,... ) чи1,2,3,... . В області частот 4 4 зосереджено більше 95%
енергії спектра. Звідси можна прийняти, що |
4 і |
F |
|
4 |
|
2 |
. |
||
|
|
||||||||
|
m |
|
m |
|
2 |
|
|||
|
|
|
|
|
|
||||
Оскільки весь інтервал кутів 2 , то |
F 2 |
2 |
2 8 . Ми |
||||||
|
|||||||||
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
отримали, що для ідентифікації того, що на кожному радіусі яскравість L0 постійна, достатньо на окружності цього радіуса взяти 8
точок відліку. Отже, загальна кількість точок відліку для ідентифікації форми «круглої» функції L(r, ) постійної яскравості буде
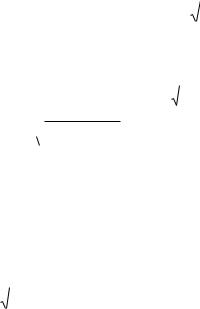
дорівнювати (рис. 55 ):
N 1 2Frmr0 2F m 2 1 3 8 25 .
Рис. 55
- 61 -
Загальна кількість інформації, яка може бути отримана в результаті ідентифікації форми та яскравості круглого джерела, якщо вимірювальна система фіксує кожний фотон випромінювання, що проходить (тобто працює в режимі підрахунку фотонів), визначиться виразом:
IL IФ 25log2 (1 )1/ 2 , |
(2.104) |
|||||
де - |
N 2 |
|
, |
N - середня кількість фотонів, що випромінюються |
||
N 2 |
||||||
|
|
|
|
|||
елементарною |
|
площадкою об’єкта, N 2 |
- дисперсія часових |
|||
флуктуацій цих фотонів.
- 62 -
|
|
|
|
|
|
|
ДОДАТОК №1 |
|
|
||||||
Розклад поля сферичної хвилі по плоских хвилях. |
|
||||||||||||||
|
|
|
|
|
|
|
АФЧАФ вільного простору |
|
|||||||
Нехай |
задана |
комплесна |
|
амплітуда |
сферичної |
хвилі |
|||||||||
|
|
exp(ikR) |
|
|
|
|
|
|
|
|
|
||||
(x, y, z) |
, |
де R |
|
x2 y2 z2 , |
то кожна |
точка |
|||||||||
|
|
||||||||||||||
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
площини x, y,0 випромінює сферичну хвилю. |
|
|
|||||||||||||
Поле в площині x, y, z визначається відомими перетворенням: |
|||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
) exp i(kx x k y y) dkx dk y , (1) |
|||||
(x, y, z) |
|
|
g(kx , k y ) exp(zi k 2 |
kx2 k y2 |
|||||||||||
4 |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
де exp(zi
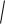k 2 kx2 ky2 ) - АФЧПФ вільного простору.
Кутовий спектр g(kx , ky ) |
визначиться Фур’є перетворенням поля |
||||||||||
в площині z 0 . Для плоскої хвилі |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
g(kx , ky ) |
(x, y,0) exp i(kx x ky y) dxdy. |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Поле |
в площині z 0 |
буде таким: (x, y,0) |
exp(ikr) |
, |
|||||||
|
|||||||||||
|
|
|
|
|
|
|
|
|
r |
||
|
|
|
|
|
|
|
|
|
|
|
|
r x2 |
y2 . |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
exp(ikr) |
exp i(kx x ky y) dxdy. |
|
|
||
g(kx , ky ) |
|
(2) |
|||||||||
|
|||||||||||
|
|
|
|
|
|
r |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
Введемо нові змінні: |
|
|
|
||||||||
kx q cos , |
k y q sin |
|
|
|
|||||||
x r cos , |
|
y r sin , |
|
|
|||||||
Враховуючи, що dxdy rdrd ,
cos cos sin sin cos( ).
Перепишемо інтеграл (2) у такому вигляді:
g(kx , k y ) exp(ikr)J0 (qr)dr.
0
- 63 -
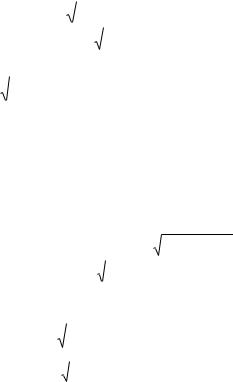
Врахуємо, що |
|
|
|
|
|
|
|
|
|
|
|
|
p |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
2 |
2 |
||||||||||||
exp(t)J p (t)dt |
|
|
|
|
|
|
|
|
|
|
|
|
, |
|||||||
p |
2 |
2 |
|
|||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|||||||||||
g(k |
|
, k |
|
) |
|
|
2 |
|
|
|
|
|
2 |
. |
|
|
(3) |
|||
x |
y |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
i k 2 k 2 |
k 2 |
|
|
ik z |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
||
Зауважимо, що в області малих значень kx , ky , тобто малих кутів |
||||||||||||||||||||
поширення хвилі відносно осі |
z ) g(kx , ky ) const , в області кутів, |
|||||||||||||||||||
коли k 2 |
|
k |
2 k 2 |
(кути |
|
) g(k |
x |
, k |
y |
) зростає, переходячи надалі |
||||||||||
x |
|
|
|
y |
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в область неоднорідних хвиль. Підставляючи (3) в (1), отримаємо:
|
|
|
|
|
|
|
2 |
2 |
2 |
|
|
|
|
|
exp(ikR) |
|
1 |
exp i(kx x k y y z |
k |
|
kx |
k y ) |
|
|
|
|
|||
|
|
2 |
|
|
|
|
||||||||
|
|
2 2 |
|
|
|
dk |
x |
dk |
y |
. |
||||
R |
i2 |
|
|
|
|
|
|
|||||||
|
k kx ky |
|
||||||||||||
|
|
|
|
|
|
|
|
|
||||||
Що і є поданням сферичних хвиль через сукупність плоских. |
|||||||||||
Знайдемо Фур’є спектр АФЧПФ: |
|||||||||||
|
|
|
|
|
) exp iz |
|
|
|
|
. |
|
W (ik |
x |
, ik |
y |
k 2 k 2 |
k 2 |
||||||
|
|
|
|
|
|
x |
y |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
exp iz |
|
|
|
exp i(kx x ky y) dkx dky . |
||||
w(x, y) |
|
|
k 2 kx2 |
ky2 |
|||||||
|
2 |
||||||||||
|
|
|
4 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
(4)
(5)
w(x, y) |
- функція ваги вільного простору. Функуція ваги |
w(x, y) |
|||
дозволяє |
визначити поле |
в площині |
x, y, z , |
якщо відоме |
поле в |
площині x, y,0 . |
|
|
|
|
|
Нехай розподіл комплексних амплітуд в площині x x0 , y y0 , z |
|||||
визначається функцією |
E(x0 , y0 ,0) , |
тоді |
у площині |
x, y, z |
|
комплексна амплітуда E(x, y, z) визначиться виразом
E(x, y, z) E(x0 , y0 ,0)w(x x0 , y y0 )dx0 dy0 .
Для розрахунку інтегралу (5) продиференціюємо (4) за змінною z .
- 64 -
|
|
|
exp(ikR) |
|
|
|
|
|
1 |
|
|
exp iz |
|
|
|
|
|
|
exp i(kx x ky y) dkx dky . |
|
|||||||||||||||||
|
( |
) |
|
|
k 2 kx2 ky2 |
(6) |
|||||||||||||||||||||||||||||||
|
z |
|
|
|
2 |
|
|
||||||||||||||||||||||||||||||
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Порівнюючи (5) і (6) маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
w(x, y) |
|
1 |
( |
exp(ikR) |
) |
1 |
ik |
exp(ikR) |
R |
|
1 |
|
1 |
exp(ikR) |
R . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
2 z |
|
|
|
|
|
|
|
2 R2 |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
R |
2 |
R |
z |
|
|
|
z |
||||||||||||||||||||||
При R другим членом можна знехтувати, а |
R |
|
z |
cos . |
|
||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
R |
|
|
|||
|
w(x, y) |
|
1 |
ik |
exp(ikR) |
cos |
1 |
|
|
exp(ikR) |
cos . |
|
|
||||||||||||||||||||||||
|
|
|
|
i |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
R |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|||||||||||
Поле E(x, y, z) |
|
визначається так: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
exp(ikR) |
|
|
|
|
|
|
|
|
|
|
|||||||
|
E(x, y, z) |
|
|
|
E(x0 , y0 |
,0) |
cos dx0 dy0 , |
|
(7) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
де R 
(x x0 )2 ( y y0 )2 z2 .
|
Тобто при опроміненні об’єкта в площині x0 , y0 ,0 |
когерентним |
|||||||||||||||||||||
пучком у площині x, y, z |
формується поле (безопорна голограма) від |
||||||||||||||||||||||
кожного елемента dx0 , dy0 |
відповідно до теорії дифракції. |
|
|||||||||||||||||||||
|
Функцію |
|
|
|
|
exp ik |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
w(x x |
|
, y y |
|
) |
1 |
ik |
(x x0 )2 ( y y0 )2 z 2 |
cos |
|||||||||||||||
0 |
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
(x x0 )2 ( y y0 )2 z 2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 exp ik |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
(x x0 )2 ( y y0 )2 z 2 |
cos . |
|
|
|
|||||||||||||||||
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
(x |
x0 )2 ( y y0 )2 z 2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
називають функцією Френеля-Кіргофа-Зоммерфельда.
- 65 -
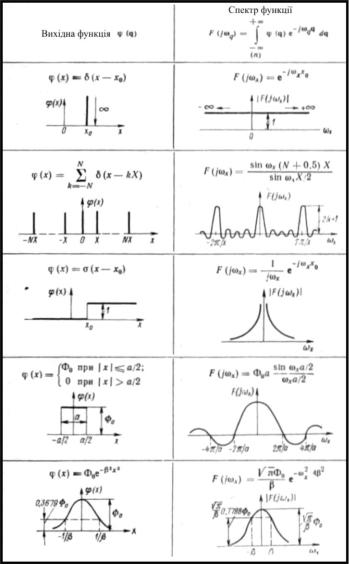
ДОДАТОК №1
Завдання
- 66 -
- 67 -
- 68 -
- 69 -
- 70 -