
FOKOEP_-_CHastina_2
.pdf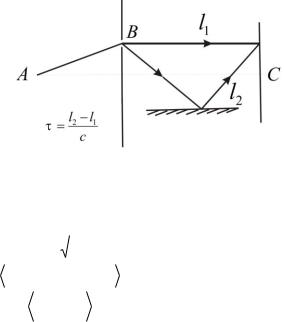
що функція 12 ( ) у загальному випадку характеризує об’єм
когерентності.
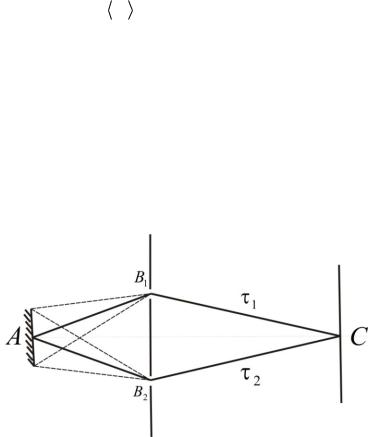
Розглянемо сутність часової когерентності. Нехай точка С на екрані освітлюється двома пучками, які отримуються від одного джерела при використанні дзеркала (рис. 39).
Рис. 39. Уведення часової когерентності з часовою затримкою
Така схема еквівалентна схемі інтерферометра Майкельсона з напівпрозорим світлоподільником.
У даному випадку інтенсивність у точці С описується виразом
|
|
|
|
|
|
|
Re |
11( ) , |
|
|||
IC I1c |
I2c |
2 I1c IC |
(2.35) |
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|||
де 11( ) |
|
E |
1 |
(t )E* 1 (t) |
|
|
||||||
|
|
|
|
|
|
|
|
. |
|
|
||
|
|
|
|
E 1 (t) |
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Функція 11( ) описує кореляцію одного хвильового випадкового процесу в точці В у моменти часу, рознесені на інтервал . У зв’язку
з цим |
функція 11( ) |
(чи просто ( ) ) характеризує часову |
когерентність. |
|
|
При цьому функція 11( ) однозначно визначається спектром
потужності хвильового процесу. Можна показати, що
Re 11( ) f ( ) cos( )d ,
0
- 21 -
де f () |
I ( ) |
|
, |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
I ( )d |
|
|
|
|
||
|
0 |
|
|
|
|
|
|
I ( ) - спектральна густина випромінювання. |
|
|
|||||
Косинусне Фур’є-перетворення від величини Re 11( ) |
дозволяє |
||||||
визначити сам спектр I ( ) . Це лежить в основі Фур’є-спектроскопії. |
|||||||
Характерно, |
що |
часова |
когерентність, |
яка |
враховує |
||
скорельованість випромінювання само з собою в різні моменти часу, буде залежати від ширини спектра випромінювання. Останній буде задавати інтервал t , протягом якого випромінювання можна вважати скорельованим.
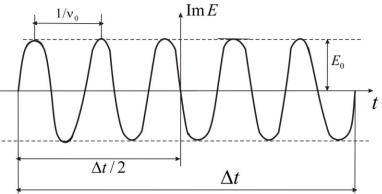
Розглянемо просторову модель випромінювання у вигляді випадкових цугів однакової протяжності. Цуг - аналітичне представлення хвильового процесу, коли фаза в наступний момент визначається попереднім моментом.
Нехай деяке джерело випромінює хвильові цуги однакової протяжності (в часі) t на частоті 0 2 0 .
Представимо в аналітичній формі випромінювання такого цугу:
E exp(i2 |
|
t) |
при |
|
t |
|
t / 2. |
|
||
|
|
|
|
|||||||
E(t) |
0 |
0 |
|
|
|
t |
|
|
t / 2. |
(див. рис. 40). (2.36) |
|
|
|
|
|
||||||
|
0 |
|
|
при |
|
|
|
|
||
Рис. 40. Зображення монохроматичного цугу протяжністю t
- 22 -
Застосовуючи перетворення Фур’є до функції E(t) , отримаємо:
|
|
|
|
|
|
E( ) E(t) exp( 2i t)dt |
|
|
|
|
|
|
|
|
|
|
|
E0 |
t / 2 |
sin 2 ( |
|
) t |
. |
exp( 2i( 0 )t)dt E0 t |
|
0 |
2 |
||
|
|
|
|
|
|
|
|
( 0 ) t |
|
||
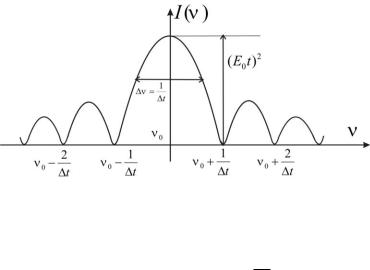
Інтенсивність такого гармонічного процесу визначиться виразом |
|||||||
I ( ) (E t)2 |
sin2 ( |
0 |
) t |
(див. рис. 41). |
(2.37) |
||
( 0 ) t 2 |
|
||||||
0 |
|
|
|||||
Рис. 41. Спектральна густина інтенсивності монохроматичного цугу протяжністю t
Частотний інтервал , який відповідає напівширині контуру спектральної лінії, де інтенсивність ще достатньо велика (не менше
0,4I
(
max ) визначиться співвідношенням 1t .
sin |
2 |
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0.4, |
коли |
t / 2 ). |
||
|
|
|
|
2 |
|
2 |
||||
|
|
|
t |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Звідси випливає таке правило: ефективна смуга частот хвильового цугу обернено пропорційна його протяжності. Довжина
- 23 -
L c t c |
1 |
буде відповідати максимальній різниці ходу, коли |
|
|
|||
|
|
зберігаються фазові співвідношення в інтерференційному досліді. При
різниці ход, суттєво більшій ніж |
c |
1 |
, спостереження |
|
|||
|
інтерференційної картини стає неможливим.
Розглянутий механізм випромінювання сильно ідеалізований. У дійсності мають місце процеси затухання випромінювання, статистичного розподілу довжин і амплітуд цугів, зміни фази цугу через співударяння атомів, зміна частоти у зв’язку з тепловим рухом.
Розглянемо, до чого приводить процес випромінювання із затуханням, що пов’язано із суттєвою втратою енергії в часі, в результаті чого амплітуда хвильового цугу зменшується в часі:
|
|
|
|
|
t |
|
|
t 0. |
|
E |
|
exp(i2 |
|
t |
|
) |
при |
(2.38) |
|
|
|
|
|||||||
E(t) |
0 |
|
0 |
|
|
при |
t 0. |
||
|
|
0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Частотний спектр Фур’є такого процесу визначається виразом
|
E0 |
|
||
E( ) E0 exp( 2 i( 0 )t t / )dt |
. |
|||
2 i( |
0 )t 1/ |
|||
0 |
|
|||
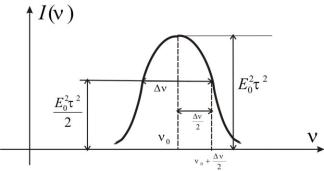
Спектральна інтенсивність такого цугу буде такою:
I ( ) |
|
E( ) |
2 |
|
|
E 2 |
|
|||
|
|
|
|
0 |
. |
(2.39) |
||||
|
|
4 |
2i( |
0 |
)2 t 1/ 2 |
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
Рис. 42. Спектральна інтенсивність затухаючого цугу (Лоренцовий контур)
- 24 -
Напівширина контуру лінії визначається з умови:
|
|
|
1 |
|
|
|
2 |
, звідси |
1 |
. |
|
4 |
2 |
|
2 |
1/ |
2 |
2 |
|
||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
|
|
|
Якщо реальний хвильовий процес охарактеризувати середньостатистичним часом t , що відповідає напівширині контуру, то можна ввести поняття довжини когерентності, в межах якої зберігаються фази цугів хвиль, що проходять.
l |
|
tc |
c |
|
0 |
2 |
. |
k |
|
|
|
||||
|
|
|
|
|
|||
|
|
|
|
|
|
З (2.40) випливає, що довжина когерентності чисельно дорівнює максимальній кількості смуг стаціонарної інтерференційної картини, помноженій на середню довжин хвилі в спектрі.
Поняття часу когерентності та довжини когерентності еквівалентні.
2.2.1. Поняття просторової когерентності
Повернемось до розгляду інтерференційного досліду з двома отворами, коли точка «С» вибрана так, що часова затримка
2 1 0 (рис. 43):
Рис. 43. Введення просторової когерентності
- 25 -
У такому випадку відносна функція взаємної когерентності12 (0) , дійсна частина якої визначає сумарну інтенсивність, визначиться усередненням
|
|
(0) |
E 1 E* |
2 |
(t) |
|
|||
12 |
|
|
|
|
|
. |
(2.41) |
||
|
|
|
|
|
|||||
|
|
|
|
||||||
|
|
|
|
I B |
I B |
|
|||
|
|
|
1 |
|
2 |
|
|
|
|
У теорії когерентності доводиться, що числове значення 12 (0) пов’язане з кутовою розбіжністю випромінювання чи кутовими розмірами протяжного джерела.
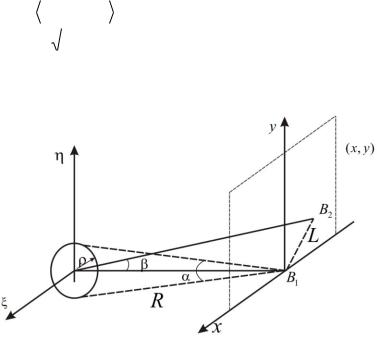
Рис. 44. Геометричні параметри, що визначають просторову когерентність від круглого дзеркала радіусом .
Для протяжного випромінювача, утвореного ансамблем статично незалежних елементарних випромінювачів, просторова когерентність розраховується на основі теореми Ван-Циттера-Церніке.
Так, для круглого теплового джерела, розміщеного в площині, постійна яскравості, ступінь когерентності у двох точках B1 та B2 ,
що знаходяться на відстані R, що набагато більше від радіуса джерела ρ (рис. 44), розраховується згідно з формулою.
|
|
12 |
(0) |
|
2 |
J1 (z) |
, |
(2.42) |
|
|
|||||||
|
|
z |
||||||
|
|
|
|
|
|
|
|
- 26 -
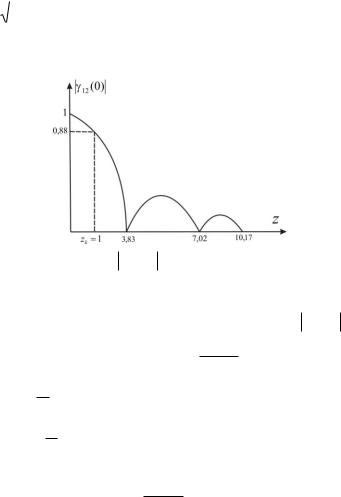
де J1 (z) |
– |
функція |
Бесселя першого роду аргументу |
|||||
|
|
|
/ R 2tg . |
|||||
z 2 x2 |
y2 |
|||||||
|
|
|
|
|
|
|
|
|
Графік функції |
|
12 (0) |
|
|
наведено на рис. 44а. |
|||
|
|
|||||||
Рис. 44а. Функція 12 (0) в залежності від параметра z
Висока ступінь когерентності можлива тільки для малих кутів β. Лінійна відстань L, що відповідає значенню 0 12 (0) 1, не
повинна перебільшувати величини L 0.16 , де – кутовий радіус
джерела ( R ).
Якщо RL – кутова розбіжність променів джерела, то кут розбіжності практично когерентного пучка не повинен
перебільшувати величини 0.16 , де – радіус джерела.
Можна зробити висновок, що з когерентністю випромінювання, яка характеризується комплексними функціями 12 ( ) , 11( ) ,12 (0) , пов’язані такі характеристики випромінювання як монохроматичність і розбіжність випромінювання. При цьому
- 27 -

враховують, що всі компоненти когерентного випромінювання мають однакові стани поляризації (лінійні чи еліптичні). Плоска монохроматична хвиля завжди поляризована.
На практиці зручно пов’язати ступінь когерентності з контрастом інтерференційної картини, що вимірюється в площині її спостереження. Величина контрасту визначається співвідношенням
K |
(Imax Imin ) |
. |
|
|
|
|
|
(2.43) |
||
|
|
|
|
|
|
|
|
|||
|
(Imax Imin ) |
|
|
|
|
|
|
|||
Представив реальну частину |
функції 12 ( ) |
|
у |
вигляді |
||||||
Re 12 ( ) |
|
|
|
Im |
12 |
( ) |
|
|||
|
|
|
|
|||||||
12 ( ) |
cos( ) , де |
( ) arctg |
|
|
|
|
- її |
|||
|
|
|
|
|
Re 12 |
( ) |
|
|||
аргумент, вираз для інтенсивності результуючої інтерференційної картини можна записати так:
I I1 I2 2
 I1I2 12 ( ) cos( ).
I1I2 12 ( ) cos( ).
При введенні середньої частоти фазовий множник
результуючої інтерференційної картини подається так:
( ) ( ) 2 ,
чи
( ) ( ) 2 ,
де ( ) , ( ) - функції, що характеризують зміну усередненої фази для сукупності квазімонохроматичного інтервалу в залежності від часу чи різниці ходу. Зауважимо, що зміна величин ( ) та ( )
несуттєва у порівнянні з величинами 2 чи 2 .
Для двох найближчих екстримальних значень інтенсивності, що отримуються коли cos( ) 1, будемо мати:
I max |
I1 I2 |
2 |
|
I1 I2 |
12 |
( ), |
||
|
|
|
|
|
|
|
|
(2.44) |
I min |
I1 I 2 |
2 |
I1 I 2 |
12 ( ). |
||||
Звідки
- 28 -
|
|
|
|
|
|
|
|
|
|
|
|
K |
2 I1I2 |
12 |
( ) |
. |
|
|
|
|
|||
|
I1 I |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
Якщо I1 I2 |
|
, то K |
|
12 ( ) |
|
. |
|||||
|
|
|
|||||||||
З вищевикладеного випливає, що основною відмінністю когерентного випромінювання від монохроматичного є введення усереднених амплітуд E(t) і фаз (t) для сукупного спектрального
інтервалу на деякій усередненій частоті 0 , що є функціями, які повільно змінюються при аргументах t 1 . При цьому при
складанні двох полів, інтерференційна картина стає менш контрастною за рахунок усереднення миттєвої інтенсивності по часу.
2.2.2. Фазові та групові швидкості в середовищі
Якщо в деякій початковій точці однорідного, ізотропного діелектричного середовища сумарна напруженість плоскої хвилі (без врахування поляризації) задана виразом
E (t) E(t) exp(i(0t (t))) , |
|
|
|
|
|
|
|
|
|
|
|||||||||||
то в точці, що визначається |
радіусом |
||||||||||||||||||||
r , ця напруженість |
|||||||||||||||||||||
запишеться таким чином: |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
rn |
|
||||||
E (r , t) E(t) exp i (t) exp |
i 0 |
(t |
|
|
|
|
|
|
) |
||||||||||||
|
|
|
|
|
|
||||||||||||||||
E(t) exp i (t) exp i( |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
t k ' |
r ) |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||
де |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k0' k0 k ; k0' |
|
|
; k0 |
|
0 |
|
|
|
2n(k |
0 |
) |
|
|||||||||
0 |
|
|
|
|
|
|
|
|
|
|
, |
||||||||||
|
(k0 ) |
|
0 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
- середня швидкість для груп хвиль із напівшириною спектра |
||||||||||||||||||||
, |
(k0 ) - фазова швидкість хвильового вектора в середовищі з |
||||||||||||||||||||
довжиною хвилі |
, k |
|
|
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
- 29 -
Очевидно, що k k ; k k |
k |
k |
|
, |
|
|
k |
0 |
|
|
|
|
|
|
0 |
|
|
де k - напівширина спектрального інтервалу задана у хвильових
числах. Отже,
E (r ,
|
|
|
|
|
|
t) E(t) exp i (t) kr |
exp i( 0t k0r ) . |
|
Вираз (2.45) дозволяє знайти фазову чи групову швидкість |
|
|
|
сумарних коливань уздовж хвильвої нормаі. Коли r // n, k , маємо:
E (r, t) E(t) exp i (t) kr exp i(0t k0r) .
Взявши похідну по часу від умови постійності фази на несучій
частоті 0 отримаємо |
|
|
|
|
|
|
|
|||||||
|
d |
( |
t k |
r) const , |
|
0 |
. |
|||||||
|
|
ф |
||||||||||||
|
dt |
|
0 |
|
0 |
|
|
|
k0 |
|
|
k |
||
|
|
|
|
|
|
|
|
|
|
|
||||
Групова швидкість визначиться з умови постійності амплітуди в |
||||||||||||||
просторі, тобто (t) kr const . |
|
|
|
|||||||||||
|
|
|
|
dr |
d (t) |
|
|
|
d |
|
||||
гр |
|
|
|
|
|
/ k |
k |
|
|
|
. |
|||
dt |
|
|
dk |
|||||||||||
|
|
|
|
dt |
|
|
|
|
||||||
Коли |
в |
середовищі характерна |
дисперсія, |
|
тобто |
n n( ) , |
|||||||||||||||||||||||||||
n n(k) , то ф гр . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Враховуючи |
співвідношення |
|
k |
|
, |
|
dk |
d |
d |
, |
|||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||
d dk |
d , |
|
групова |
швидкість |
|
|
визначиться |
|
такими |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
дисперсійними співвідношеннями: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
d |
|
|
2 d |
, k |
|
|
2 |
|
, |
dk |
|
2 |
, |
||||||||||||
|
|
|
|
|
d ф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
. |
|
dk |
|
dk |
|
|
|
d |
2 |
|||||||||||||||||||
гр |
ф |
d |
|
d |
|
|
d |
|
|
|
dk |
|
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
, |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
dk |
d |
|
d |
|
|
d |
|
|
|
|
|
|
|
||||||||||||
Для діелектриків поза смугою поглинання ф |
гр , а у смузі |
|
поглинання ф |
гр . |
|
|
- 30 - |
|
