Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черновицкий национальный университет им. Ю. Федьковича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

FOKOEP_-_CHastina_1

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

1.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Перший доданок дорівнює нулю згідно з умовами представлення

функції інтегралом Фур’є, тобто (x) 0 при x . Тому


F1 (i x ) i x (x)e i x x dx i x F (i x ),	(69)

тобто спектр похідної дорівнює спектру вихідної функції, помноженої на i x (чи i2fx у представленні зворотних частот).

1.3.9. Теорема про спектр інтеграла

Нехай спектр функції (x) дорівнює F(i x ) . Знайдемо спектр F1 (i x ) інтегралу від заданої функції в межах від до Х, тобто

1 (x) (x)dx. За умови, що

(x) (x)dx 0.

Після послідовних перетворень:

i x x

F1 (i x ) ( (x)dx)e i x x

( (x)dx)

i x

використовуючи інтегрування частинами отримаємо:

i x x

F1 (i x ) (

(x)dx)

(x)dx,

i x

Отже, спектр інтегралу заданого функцією дорівнює її спектру,

поділеному на i x :
F (i	)	1	F (i	) .	(70)

1 x			x
		i x

1.3.10. Двовимірне перетворення Фур’є, перетворення Ганкеля

При аналізі роботи ОЕС дуже часто вхідні та вихідні сигнали визначаються на площині у вигляді функцій, що залежать від

- 41 -

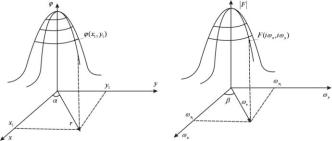
прямокутних (x, y) чи полярних (r, ) координат. Використання

полярних координат для знаходження просторово-частотного спектра сигналу переважає та зумовлює перетворення Ганкеля.

Нехай є перетворення Фур’є від двовимірної функції (x, y) , заданої у прямокутній системі координат (x, y) :


F (i x , i y ) (x, y)e i( x x y y) dxdy.	(71)

Перейдемо до полярної системи координат у просторі предметів, як і в просторі просторових частот відповідно до таких рівностей:

x r cos ,

y r sin ,

1/ 2

arctg (

(72)

)

;

1/ 2

(73)

x r cos ,

y r cos ,

r ( x

)

;

arctg(

Рис. 18. Двовимірна функція (x, y) та її двовимірний спектр у декартовій системі координат

Підставляючи		(72), (73) у		інтеграл (71), враховуючи, що
dxdy rdrd , після перетворень, отримаємо:
			2
F (i r , ) rdr			(r, )e ir r cos( ) d .		(74)
	0		0
Підставимо функції (r, )				та F(i r , ) у вигляді	таких
добутків:
(r, ) in (r)ein ,					(75)
F (i	, ) F (		)ein .		(75)
F (i	, ) F (		)ein .
r		r

- 42 -

п – цілі числа (п = 0, 1, 2…).

При підстановці (75) в (74), позначивши , d d , отримаємо:

F ( r ) i

Згідно з

	2
n r (r)dr e i(r r cos n ) d .
0	0
		i n	2
визначенням, вираз		2		e i(r r c o sn ) d J	n	(	r)	є
визначенням, вираз				e i(r r c o sn ) d J		(	r)	є
						r
			0

функцією Бесселя п-го порядку від аргументу ( r r) . У зв’язку із цим маємо:


F ( r ) 2 r (r)Jn ( r r)dr.									(76)
		0
Формула (76) називається перетворенням Ганкеля. Зворотне
перетворення Ганкеля матиме вигляд

(r) r F (r )Jn (r r)d r .									(77)
	0
Повне значення функції (r, ) на основі (75), (77) буде таким:

(r, ) i nein F (r ) r Jn (r r)d r .									(78)
				0
Значення функції F(i r , ) ,					відповідно до повного перетворення
Ганкеля,	що		визначається		у	просторі		кругової частоти
2	2	1/ 2					y
r (x	y	)		та напрямком		arctg (		) ,	на основі (75) та
r (x	y	)		та напрямком		arctg (	x	) ,	на основі (75) та
							x
(76), буде:

F (i r , ) 2 ein r( (r))Jn ( r r)dr.									(79)
				0
Якщо функція (r, ) симетрична відносно координати r 0 , то
її форма повністю повинна визначатися радіусом									r , що можливе,
коли n 0 . Тому,			якщо (r, ) (r) , то F(i r , ) F(r ) . Згідно

із (76) та (77), отримаємо пару симетричних перетворень Ганкеля:

- 43 -

F ( r ) 2 (r)rJ0 ( r r)dr,

(80)

(r) F (r ) r J0 (r r)d r ,

(81)

де J

(

2 e i r r cos ) d - функція Бесселя нульового порядку.

1. 3. 11. Узагальнення основних властивостей п-вимірних

перетворень Фур’є

Спектр Фур’є функції

Висхідна функція (x)

i x x

F (i x )

(x)e

dx.

( n )

a1 1(x)

a2 2 (x)

a1F1(i x ) a2 F2

(i x )

d (m)

(m)

(x)

(i x ) F1 (i x )

(x)

1 (x)dx

(i x ) m F1 (i x )

( m )

F (i

)e i x y

(x' ) 2

(x x

' )dx

(2 )n

(i x )F2[i(x

x )]d

( n )

(x)

2F (i '

) cos(

x )

2F (i '

) sin(

x )

1 (x x1 ) 1 (x x1 )

(2 )

F1 (i x )

d x

- 44 -

1.3.12. Зміна масштабу та поворот системи координат при Фур’є-перетворенні.

При розрахунку ОЕС часто виникає необхідність перетворення

векторного аргументу x	функції (x) , пов’язаного зі зміною

масштабу чи поворотом системи координат. Розглянемо, як знайти спектр функції після того, як здійснено перетворення її аргументу.

Нехай задана функція та знайдено її спектр Фур’є:

)

(

F (i x ) (x)e i x x dx.

( n )

Здійснимо лінійне перетворення п-вимірного аргументу x у п-

вимірний аргумент z згідно з правилом:

(82)

z ,

aik

(i, k 1,2...n)

- n n -вимірна

матриця коефіцієнтів

де A

перетворення;

Ak ,i

- n n -вимірна матриця, зворотна матриці A ;

det A

det A - визначник матриці A ;

Ak ,i - алгебралічне доповнення елементів aik

прямої матриці A .

Спектр

функції

після

перетворення в

ній аргументу x

запишеться так:

аргумент z

F (i z ) (z)e i x x

( n )

dx.

Після підстановки x

F (i z ) (z )e i

( n )

	ˆ		1
	A			z , отримаємо:
ˆ 1				ˆ	1
x A	z					z).	(83)
		d ( A

Із векторної алгебри відомий такий вираз для диференціалу:

	ˆ	1		ˆ	1
dx	d( A		z) det A		dz

- 45 -

(x1, y1 )

ˆ 1

та справедлива перестановка x

. На основі чого (83)

запишеться у вигляді:

ˆ 1

(z)e

izA

F (i z ) det A

d (z) det A

F (iA

x ).

(84)

( n )

Із (84) випливає

таке

правило:

якщо

задана

функція

(x) і

знайдений її спектр F(i x ) , то для знаходження спектра F(i z )

функції необхідно помножити модуль початкового спектра на

)

(

	ˆ	1
			, а аргумент	x	у просторі частот - на саму
визначник матриці A
ˆ 1	.
матрицю A

Приклад

Нехай у прямокутній системі координат задана функція (x, y) , спектр Фур’є якої дорівнює F(i x , i y ) . Перетворимо функцію у

другу із прямокутною системою координат (x1, y1 ) , яка буде відрізнятись від попередньої лише зміною масштабу (поворот відсутній): (x1, y1) (ax x, ay y) . Зв’язок між координатами

та (x, y) при цьому біде визначатись матричними рівняннями:

(85)

тобто

ˆ 1

;

det A

ax ay ;

; det A

ax ay

Спектр Фур’є

F(i x

, i y

) функції (x1, y1 ) , згідно з (84), буде

такиме:

F(i x , i y )

F(i

x , i

) .

(86)

ax ay

- 46 -

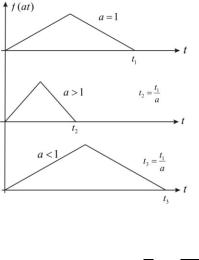
Зверенемо увагу на те, що при лінійному перетворенні z ax ; коли a 1, спостерігається стиснення сигналу; коли a 1 - сигнал розтягується, що показано на рис. 18.

Рис. 18.

Водночас відповідні спектри F (i z ) 1a F (i ax ) поводять себе

протилежно. Тобто при стисненні синалу спектр розтягується та навпаки.

Здійснимо поворот системи координат від початкової проти годинникової стрілки на кут без зміни масштабу. Тоді зв’язок між

функціями (x, y)

та (x1, y1 ) визначиться так:

cos

sin

cos

(x1, y1 ) (x cos y sin , x sin y cos ) .

cos

sin

cos

;

det A 1 ,

cos

sin

cos

; det A

- 47 -

Частотний спектр у новій системі координат буде матиме вигляд:

cos

sin

F (i x ,i y

) F i

(87)

sin

cos

F i( x cos y sin ),i( x sin y cos )

Отже, при повороті системи координат заданої функції проти

годинникової

стрілки на

кут

частотний спектр

нової функції

F(i x ,i y )

відповідає

частотному

спектрові

F(i x ,i y ) при

повороті

його

просторових

частот

,y )

за

годинниковою

стрілкою.

1.3.13. Функції із обмеженим спектром. Теорема Котєльнікова

При передачі реальних сигналів їх спектр завжди обмежений значенням смуги пропускання частотного тракту ОЕС. Обмеження за спектром приводить до того, що відповідні сигнали можуть бути визначені кінцевою кількістю значень протягом кінцевого інтервалу. Ця особливість випливає з теореми В.А. Котєльнікова: якщо функція

(x) не містить частот, більших ніж fxm , то вона повністю визначається шляхом задання її ординат у послідовних точках, які

знаходяться на відстані одна від одної.

2 fxm

Доведення У загальному випадку

(x) F (if x )ei 2 fx x dfx ,

де

F (if x ) (x)e i 2 fx x dx.

- 48 -

Оскільки функція F (if x ) з обмеженим спектром, то при fx fxm ,

		fxm
F(if x )	0 , F(if x ) 0 та (x)	F (if x )ei 2 fx x dfx .


		fxm

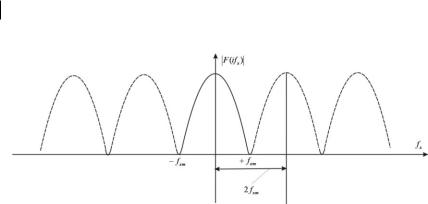
Рис. 19. Представлення функції з обмеженим спектром періодичної функції з періодом 2 f xm

Оскільки межі інтегрування обмежують наступний розгляд інтервалом fxm fxm , то припустимо, що функція F (if x ) періодично повторюється з періодом 2 fxm (рис. 19):

F(if x ) F[(i( fx 2 fxm )].

Тоді цю періодичну функцію можна подати рядом Фур’є:

1 k

2 kfx

(2 fmx )

F (if x )

Ak e

2 k

де

fxm

2 kfx

(2 fmx )

F (if x )e

dfx .

(2 f

)

fxm

При x

маємо:

(2 fxm )

fxm

2 kfx

(2 f

)

(

)

F (if x )e

dfx

(2 fxm )

fxm

2 /(2 fxm )

- 49 -

(

(2 fxm )

Визначимо значення (x) через значення F (if x ) , що подається

нескінченним рядом:

f xm

k i

2 kf x

(x)

(

(2 f xm ) )ei 2 f x dfx .

Ak e

f xm

Після зміни порядку інтегрування та сумування отримаємо:

f xm

(x)

ei 2 f x [ x 2 f xm ]df .

2 k

f xm

i 2 f xm [ x

]

i 2 f x [ x

]

f xm

i 2 f x [ x

]

2 f xm e

2 f xm

2 f

df x

i2f xm [x

]

f xm

2 f xm

		k
(2 f xm )Sa 2f xm	(x		)
(2 f xm )Sa 2f xm	(x	2 f xm	)
		2 f xm

sin 2 fxm (x

)

2 fxm

Sa 2 fxm (x

)

(87а)

2 fxm

)

2 fxm

- функція відліків.

Відповідно:

(x) Ak

f xm Sa 2 f xm

)

(

)Sa 2 f xm

) .

2 f xm

Позначимо

та відмітимо,

що

знаки

перед

2 fxm

останньому виразі можна змінити, оскільки йде перебір у сумуванні за всіма значеннями k . Тоді остаточно матимемо:

k
(x) (k x)Sa 2fxm (x k x) .	(87б)

- 50 -

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.2016116.22 Кб12Fin_zv_1_1.doc
#
22.08.2019230.12 Кб26fitopatologiya.docx
#
14.09.2019281.86 Кб6Fizika(1).docx
#
08.11.2018285.18 Кб19fizika7_9.doc
#
28.09.201974.75 Кб3Fizyka_mag.doc
#
23.02.20161.88 Mб7FOKOEP_-_CHastina_1.pdf
#
23.02.20161.86 Mб8FOKOEP_-_CHastina_2.pdf
#
22.11.2019462.55 Кб3Fondovy_rinok_metodichka (1).docx
#
02.09.20191.13 Mб34Fotocon_SC.doc
#
23.02.2016468.01 Кб14Fotogrammetriya моє.rtf
#
23.02.201656.32 Кб29FOTOMETRIYa2014.doc