Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черновицкий национальный университет им. Ю. Федьковича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

FOKOEP_-_CHastina_1

.pdf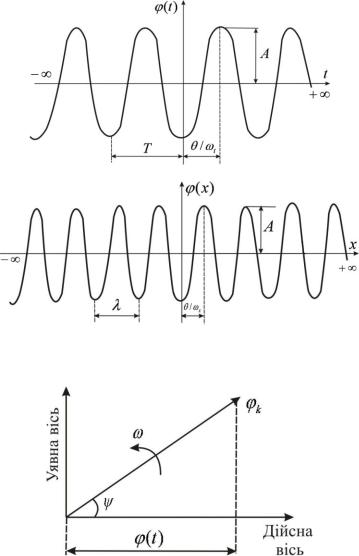

Скачиваний:

Добавлен:

23.02.2016

Размер:

1.88 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Рис. 10. Графічне зображення гармонійних коливань

Рис. 11. Комплексне представлення гармонійного коливання

- 21 -

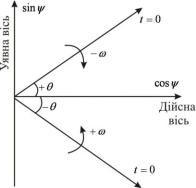
Гармонічне коливання (t) можна також розглядати як суму двох комплексних коливань k (t) і k (t) з однаковим модулем 0,5A ,

що обертаються у протилежних напрямках:

(t) k (t) k (t) 0,5Aei 0,5Ae i Acos .

Рис. 12. Комплексне представлення гармонійного коливання у вигляді суми двох комплексних коливань k (t) і k (t)

Один із доданків може трактуватись як коливання з «від’ємною»

частотою				та фазою	.	Знак «+» зазвичай
опускається.
(t)	k	(t)	k	(t) 0,5Aei	0,5Ae i
	k		k

0,5Aei( t ) 0,5Ae i( t ) 0,5Aei( t ) 0,5Ae i(( )t ) .

Б) Будь-який складний періодичний процес може бути зображений із допомогою ряду Фур’є у вигляді суми елементарних

гармонійних коливань.
	Нехай функції (x)					та (t) задані на інтервалі від	x1	до x2 ( t1
до	t2 ) і		повторюються з періодом X (чи T )				і	частотою
x		2	, t	2	.
x		X	, t		.
1		X		T
1
						- 22 -

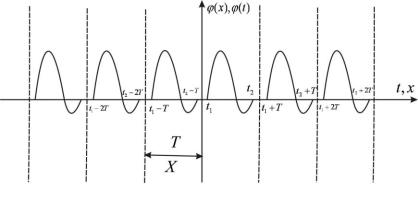
(x) (x nX ) ,

(t) (t nT ) ;

n 0,1,2...

Рис. 13. Графік періодичного сигналу

Тоді при умові, що функція (t) задовольняє умову Діріхле, тобто

має бути неперервною чи мати в межах періоду скінчену кількість розривів та максимумів і мінімумів, то її можна представити рядом Фур’є у вигляді суми тригонометричних функцій:

(x)

(an cos n x1 x bn sin n x1 x),

(41)

n 1

де

(x)dx,

(x) cos n x1 xdx,

(x) sin n x1 xdx,

причому dx може бути записаний

як dx , де

X -

протяжність одиночного імпульсу, тобто інтервал

простору або часу, в межах якого одиночний імпульс (x) 0.

Вводячи позначення

An cos n ,

An sin n ,

- 23 -

arctg (

b2 ,

вираз (41) може бути переписаний у більш компактній формі:

(x)

An (cos n x1 x n ),

(42)

n 1

що випливає з перетворення:

an cos n x x bn sin n x

An (cos n

cos n x x sin n cos n x

x) An

cos(n x x n ),

A0 a0.

Із (41) і (42) випливає, що довільний періодичний процес може бути зображений у вигляді суми гармонічних складових і визначатися

сукупностями значень An та n .

Сукупність величин An називається спектром амплітуд, а сукупність величин n - спектром фаз. Зазвичай під словом спектр

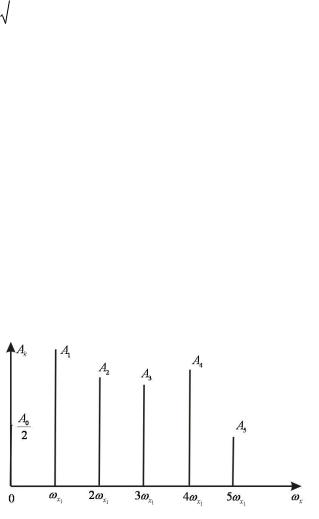
розуміють спектр амплітуд. Графічно спектр амплітуд зображається вертикальними відрізками, що відповідають значенню п-ї гармоніки.

Рис. 14. Спектр періодичної функції

Спектр періодичної функції складається з окремих ліній, які відповідають дискретним частотам 0, x1 , 2x1 , 3x1 і т. д. Слід мати

на увазі, що дискретність спектра не є ознакою періодичності функції. Спектр періодичної функції буде не тільки дискретним, а й

- 24 -

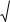
гармонічним, тобто буде складатися з еквідестантно розміщених спектральних ліній – гармонік, кратних значенню x1 .

Функції, що мають дискретні спектри з довільно розміщеними на шкалі частот спектральних ліній, називаються квазіперіодичними. Зокрема, квазіперіодичними будуть модульовані коливання, суперпозиція із двох періодичних процесів, із не кратними частотами.

Поряд із дійсною формою періодичного процесу (41), (42) велике поширення отримала комплексна форма, основою якого є представлення окремого гармонічного коливання як суми двох комплексних векторів.

Вираз An (cos n x1 x n ) можна записати так:

n 1


An (cos n x1 x n )
n 1				n 1
	An		An
	An	ei(n x1 x n )	An	ei(
	2	ei(n x1 x n )	2	ei(
n 1	2	n 1	2

ei(n x1 x n )

e i

n 1

i(n

)

Ane

n 1

(n x1

x n

x n )

) Anei(n x1 x n ) n 1

оскільки A

величина парна,

- не

парна,

b2 ,

arctg(

(x) cos n x1 xdx,

a n

a n ,

X 2

(x) sin n x1 xdx,

b n

b n .

A n A n ,

n n ,

n n .

Окрім цього, при n 0 bn

b0 0 ; n

0 0 ; e

i(n x1 x n )

Тоді вираз (42) записується так:

(x)

Anei(n x1 x n )

Ane i n ein x1 x .

(43)

2 n

Уведемо вектор комплексної амплітуди для п-ї гармоніки:

- 25 -

An Ane i n .

Отже,

1 n

(x) 2 n Anein x1 x .

(44)

(45)

Значення An

можна отримати з виразів:

An e i n an ibn

(x) cos x1 xdx i

(x)sin x1 xdx

X 2

(x)(cos n x1 x i sin n x1 x)dx

або

X 2

(x)e in x1 x dx.

(45а)

Спектр Фур’є періодичного процесу (41), (45) визначається рядом

Фур’є:

F (i x ) (x)e i x x dx

Anein x1 x e i x x dx

2 n

(46)

i(n x1 x x x)

An (n x1

x ).

Згідно з (46), спектр Фур’є періодичного процесу являє собою

суму

гармонійних

складових

комплексних амплітуд.

Фізично

результат множення

на

(x n x ) отримується за

рахунок

додавання нескінченої кількості періодично повторюваних процесів на інтервалі [ x ] .

Амплітудний спектр (46) такий:

F (i x ) An (x x1 ) (47)

Із (47) видно, що спектр Фур’є періодичного процесу визначається наявністю характерних гармонійних складових амплітудного спектра.

- 26 -

Для знаходження спектра амплітуд виразимо значення F (i x ) періодичного процесу через інтеграл Фур’є функції (x) для одного

відліку на інтервалі						X			X	чи X			X		.
відліку на інтервалі										чи X		1	X	2	.
							2					1		2
							2		2
Позначимо:
										X 2
F0 (i x ) 0 (x)e i x x dx 0 (x)e i x x dx.																(48)
										X1
Підставляючи у (48) , що n x											x , згідно з формулами (45а) та
								1
(48), маємо:
				X	.
F (i		)	A	X												(49)
F (i		)	A													(49)
0	x		n	2

Підставляючи з (49)							An	у (46), отримаємо:								(50)
F (i x ) 2				F0 (i x ) (x							n x1 ).					(50)
				n

X n

Згідно з (50), спектр амплітуд періодичної функції визначається дотичною (модулем) Фур’є перетворення одного відліку функції з

дискретизацією частот, яка дорівнює рівна n x1 x (рис. 15).

Рис. 15. Графік амплітудного спектра Фур’є періодичного сигналу

1.2.2. Спектри неперіодичних сигналів

Нехай функція (x) (чи (t) ), яку зазвичай називають сигналом, неперіодична, задовольняє умову Діріхле та абсолютно інтегрована,

- 27 -


тобто	(x)	dx N .	Це свідчить про	те, що (x)


			x . Для зручності представлення
перетворюється в нуль при
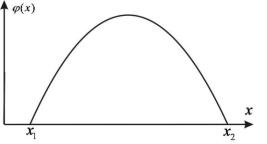
вважатимемо, що (x) відмінна від нуля на інтервалі				X1 X X 2 .

Рис. 16. Функція (x) відмінна від нуля на інтервалі X1 X X 2

Для проведення гармонічного аналізу побудуємо із функції (x) , шляхом її еквідестантного повторення із періодом X X 2 X1 , нову періодичну функцію ' (x) , розглянуту вище.

			a0
' (x)			a0	(an cos n x1 x bn sin n x1 x)
' (x)				(an cos n x1 x bn sin n x1 x)
		2		n 1					(51)
				n 1
	A				1 n
	A				1 n		in	x
	0	An		(cos n x1 x n )		Ane	x1		.
	2	An		(cos n x1 x n )		Ane	x1		.
	2	n 1			2 n

Амплітуди окремих гармонічних складових будуть тим меншим, чим більшим буде інтервал Х.

(x)dx,

(x) cos n x1 xdx,

(x) sin n x1 xdx,

(x)e

in x1 x dx.

Очевидно, що

при

X ,

(x) ' (x) . При прямуванні

періоду X до безмежності, в межах отримуються нескінченно малі

- 28 -

амплітуди гармонійних складових, а їхня кількість стає нескінченно великою на обмеженому відрізку просторових частот x , оскільки

основна частота x1 2X , при X стає нескінченно малою, як і

сама відстань між спектральними лініями буде нескінченно малою. Отримуємо відомі інтегральні перетворення неперіодичних

функцій двома способами. Маємо

1 n

1 (x)

An e

;

2 n

X 2

(52)

(x)ein x1 x dx.

Домножимо першу з нерівностей на інтервал частот

x x ,

щоб отримати умову X

1 (x)

ein x1 x x .

Переходячи

до

границі,

враховуючи,

що

X ,

x d x

0 .

Позначивши lim

An X

F (i x ) ,

n x x

та

An 0

замінюючи суму інтегралом, отримуємо:

(x) (x)

F (i )ei x x d .

(53)

Друга з рівностей (52) дає таке:

An X

lim

F (i x ) (x)e i x x dx.

(54)

Вирази (53) та (54) являють собою пару спряжених інтегральних

перетворень Фур’є, що пов’язують неперіодичну функцію (x)

з її

спектральною густиною F (i x ) , яка в загальному випадку може бути комплексною.

- 29 -

Аналогічний результат отримується при підстановці комплексної

амплітуди A в першу нерівність:

1 (x)

[

(x)e in x x dx]ein x x ein x x f x (x)e in x x d x .

При X

, (x) (x) ;

;

, а

операцію сумування перетворюється в операцію інтегрування:

(x) ei 2 f x x df x

(x)e i 2 f x x df x dx.

Позначимо внутрішній інтеграл F (if x ) :

F (if x ) (x)e i 2 f x x dx ,

тоді отримаємо

(x)

F (if x )ei 2 f x x df x .

(55)

F (if x ) -

спектральна

густина

функції

(x) , задана в шкалі

просторових

частот

( f

Звернемо

увагу

на

те, що у (55)

множник

перед

інтегралом

відсутній.

Проте при розрахунках

функції через її

спектральну густину,

задану у

шкалі просторових

кругових частот

(чи

просто кругових

частот

t ),

множник

присутній обов’язково.

Вирази

F (i x ) (x)e i x x dx;

(56)

F (if x )

(x)e i 2 f x x dx.

- 30 -

<<< < Предыдущая 1 23 / 103 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.2016116.22 Кб12Fin_zv_1_1.doc
#
22.08.2019230.12 Кб26fitopatologiya.docx
#
14.09.2019281.86 Кб6Fizika(1).docx
#
08.11.2018285.18 Кб19fizika7_9.doc
#
28.09.201974.75 Кб3Fizyka_mag.doc
#
23.02.20161.88 Mб7FOKOEP_-_CHastina_1.pdf
#
23.02.20161.86 Mб8FOKOEP_-_CHastina_2.pdf
#
22.11.2019462.55 Кб3Fondovy_rinok_metodichka (1).docx
#
02.09.20191.13 Mб34Fotocon_SC.doc
#
23.02.2016468.01 Кб14Fotogrammetriya моє.rtf
#
23.02.201656.32 Кб29FOTOMETRIYa2014.doc