
FOKOEP_-_CHastina_1
.pdf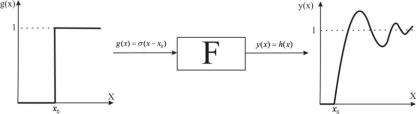
Функція y(x) h(x) , що |
визначає |
сигнал |
на виході лінійної |
системи, коли на її вхід |
поданий |
сигнал |
g(x) (x x0 ) , |
називається перехідною функцією системи. |
|
||
Між функцією ваги (x) |
і перехідною функцією h(x) існує |
||
однозначний зв'язок, що випливає із властивостей лінійності системи:
Рис. 7. Схема, що демонструє реакцію лінійної системи на сходинковий сигнал
|
dh(x) |
|
x |
|
|
|
(x) |
, |
h(x) (x)dx. |
(14) |
|||
|
||||||
|
dx |
|
|
|
||
|
|
|
|
|
||
Якщо відомі функції (x) |
та h(x) , то можна знайти реакцію |
|||||
лінійної системи |
y(x) на довільний вхідний сигнал із допомогою |
|||||
інтеграла згортки: |
|
|
||||
|
|
|
|
|
||
y(x) (x )g( )d |
(x' )g(x x' )dx'. |
(15) |
||||
|
|
|
|
|||
1.1.1. Фізичне обґрунтування рівняння згортки
Розглянемо довільний вхідний сигнал g(t) . Ми можемо розкласти довільний вхідний сигнал g(t) у послідовність імпульсів довжиною
t та амплітудою, рівною амплітуді даного сигналу в розглянуті моменти часу.
- 11 -
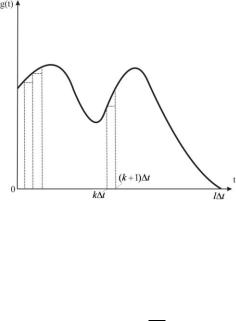
Рис. 8. Розклад довільного вхідного сигналу g(t) у послідовність імпульсів
Нехай g(0) , g(t) , g(2t) … g(k t) … - значення g(t) в моменти 0, t , 2t … k t . Позначимо через 1 (t) відгук системи
на імпульс довжиною t і амплітудою 1t . Тоді величина 1 (t) t
буде являти собою відгук системи на імпульс довжиною t одиничної амплітуди.
Тому відгук системи y0 на імпульс з амплітудою g(0) у момент часу t 0 дорівнюватиме y0 g(0) 1 (t) t .
Аналогічно відгук системи y t на імпульс з амплітудою g(t) у
момент t t буде y t g(t) 1(t t) t .
Продовжуючи підрахунок відліків системи для імпульсів у
моменти часу k t |
( k 0,1,2...l) , отримаємо такий ланцюг рівностей: |
|||||
y0 g(0) 1 (t) t |
||||||
y |
t |
g(t) |
1 |
(t t) t |
||
|
|
|
|
|
||
|
|
g(2t) 1 (t 2t) t |
||||
y2 t |
||||||
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
k t |
g(k t) |
1 |
(t k t) t. |
||
|
|
|
|
|
||
|
|
|
|
|
|
- 12 - |
Повний вихідний сигнал y(t) у довільний момент часу t від усієї
сукупності вхідних сигналів унаслідок лінійності системи визначиться сумою:
|
l |
|
|
|
|
|
|
y(t) g(k t) 1 (t k t) t. |
|
|
|
(І) |
|||
|
k 0 |
|
|
|
|
|
|
Зауважимо, що згідно з принципом причинності відгук фізичної |
|||||||
системи |
1 (t) , |
повинен дорівнювати |
нулю |
для |
t 0 , |
тому |
|
1 (t k t) 0 , |
коли t k t (результат |
наступає після дії). |
Тому |
||||
рівняння (І) можна записати у вигляді |
|
|
|
|
|||
|
|
|
|
|
|
|
|
y(t) g(k t) 1 (t k t) t, |
|
|
|
|
|||
|
k 0 |
|
|
|
|
|
|
|
|
|
|
|
|
(ІІ) |
|
|
|
|
|
|
|
||
|
g(k t) 1 (t k t) t. |
|
|
|
|
||
y(t) |
|
|
|
|
|||
|
k |
|
|
|
|
|
|
Очевидно, |
що послідовність g(k t) |
прямує |
до |
функції |
g(t) , |
||
відгук 1 (t) - |
до імпульсного відгуку системи при |
t 0 , |
тобто |
||||
1 (t) (t) . При |
t 0 суми (ІІ) |
можна замінити інтегралами, |
||
попередньо вводячи змінні k t t ' |
та t dt' . |
|||
|
|
|
|
|
y(t) |
g(t ' ) (t t ' )dt' |
|
|
|
|
0 |
' |
|
|
|
' |
|
|
|
|
|
|
|
|
y(t) |
g(t ) (t t )dt |
|
(ІІІ) |
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
y(t) g(t ' ) (t t ' )dt. |
|
|
||
|
0 |
|
|
|
|
|
|
|
|
Вирази (ІІІ) носять назву рівняння згортки. Скорочений запис y(t) g(t) (t) .
Розглянемо проходження через лінійну систему гармонійного сигналу. Такий розгляд важливий з точки зору випромінювання
динамічних характеристик системи. Сигнал g(x) gm sin(x x g )
називається гармонійним сигналом, де gm - амплітуда, x - частота,
- 13 -
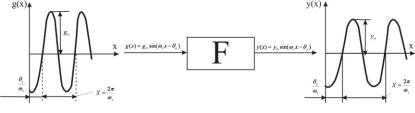
g - фаза. Оскільки в даному випадку для значення частоти x
амплітуда та фаза можуть мати різні значення, то вхідний гармонійний описується функцією
g(x) gm (x ) sin[(x x g (x )] . |
(16) |
В теорії сигналів найбільше поширення отримала комплексна форма представлення сигналу, яка значно спрощує проведення підрахунків:
g(x) G(i x ) exp(i x x) . |
(17) |
G(i x ) gm (x ) exp[i g (x )] |
- комплексна амплітуда, що |
залежить від амплітуди та фази вхідного сигналу. У відповідності до формули Ейлера, комплексна частина сигналу (17) у точності відповідає гармонійному сигналу (16):
gm ( x ) exp{i[( x x g ( x )]}
gm ( x ){cos[( x x g ( x )] i sin[( x x g ( x )]}.
Якщо на вхід лінійної системи подати гармонійний сигнал (16), то після завершення перехідних процесів у встановленому режимі сигнал на виході також буде гармонійним із тою ж частотою, проте з іншими амплітудними та фазовими значеннями:
y(x) ym (x ) sin(x x y (x )) чи в комплексній формі:
y(x) ym (x ) exp{i[(x x y (x )]} Y (i x ) exp(i x x). |
(18) |
Комплексна амплітуда Y (i x ) характеризує одночасно амплітуду та фазу вхідного сигналу.
Рис. 9. Схема, що демонструє реакцію лінійної системи на гармонійний сигнал
- 14 -
Наведена вище схема демонструє реакцію лінійної системи на вхідний гармонійний сигнал. Зміну динамічних характеристик лінійної системи у встановленому режимі при поданні на її вхід
гармонійного сигналу в залежності від частоти x можна визначити
комплексною функцією W (i x ) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
W (i x ) |
|
y(x) |
|
Y (i x ) exp(i x x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
g(x) |
G(i x ) exp(i x x) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(19) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
ym (x ) exp[i y |
(x )] |
|
|
|
y |
|
|
( |
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
m |
x |
|
exp(i ( |
|
)], |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
gm (x ) exp[i g (x )] |
gm (x ) |
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
де (x ) g (x ) y (x ) |
|
- |
різниця фаз між вхідним і вихідним |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
сигналами для заданої частоти. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Функція W (i x ) називається амплітудно-фазовою частотною |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
передаточною функцією. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Знайдемо вираз для функції W (i x ) , коли в динаміці зв'язок між |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
вхідним |
вхідним |
|
і вихідними сигналами |
|
|
визначається |
|
формулою |
||||||||||||||||||||||||||||||||||||||||||||||||
Fy {y(x)} Fg {g(x)}, |
|
а |
|
самі |
оператори |
|
Fy |
та |
|
Fg |
є операторами |
|||||||||||||||||||||||||||||||||||||||||||||
диференціювання у вигляді (4). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Тоді |
для |
|
|
вхідного |
|
гармонійного |
|
|
|
сигналу |
|
|
g(x) gm exp(i x x) |
|||||||||||||||||||||||||||||||||||||||||||
маємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[a |
|
d (n) |
|
a |
|
|
d (n 1) |
... a |
|
d |
|
|
a |
|
]y |
|
|
exp(i ) exp(i |
|
x) |
|||||||||||||||||||||||||||||||||||
|
n |
|
|
|
n |
|
n 1 |
|
|
|
n 1 |
|
|
|
|
|
0 |
m |
x |
|||||||||||||||||||||||||||||||||||||
|
|
dx |
|
|
|
|
|
dx |
|
|
|
|
|
|
1 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(20) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
[b |
|
d |
(m) |
b |
|
|
|
d (m 1) |
|
... b |
|
d |
|
|
|
b ]g |
|
exp(i |
|
x). |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
m 1 |
|
|
|
|
|
|
m |
x |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
m |
dx |
|
|
m 1 |
|
dx |
|
|
|
|
|
|
1 |
|
dx |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Проводячи |
|
|
диференціювання |
|
та |
|
|
скорочуючи |
|
на |
|
|
багаточлен |
|||||||||||||||||||||||||||||||||||||||||||
exp(i x x) , отримаємо: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
[(i |
x |
)n a |
n |
(i |
x |
)n 1 a |
n 1 |
... (i |
x |
)a |
a ]y |
m |
exp(i ) |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
(21) |
||||||||||
|
[(i |
|
)m b |
|
(i |
|
)m 1b |
|
... (i |
|
)b b ]g |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
x |
|
x |
|
x |
m |
. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
||||||||
Враховуючи, що Y (i x ) ym exp(i ) та G(i x ) gm , |
відповідно |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
до (19) Y (i x ) W (i x )G(i x ) , будемо мати: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
- 15 -
W (i |
|
) |
(i |
x |
)m b |
|
(i |
x |
)m 1b |
... (i |
x |
)b |
b |
|
|||
|
|
|
m |
|
|
m 1 |
|
1 |
0 |
. |
(22) |
||||||
x |
(i )n a |
|
(i )n 1 a |
|
... (i )a |
|
|||||||||||
|
|
|
|
a |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
n |
|
x |
|
n 1 |
x |
1 |
0 |
|
|
|
Оскільки згідно з (19) та (20) функція W (i x ) комплексна, то її |
|||||||||||||||||
можна зобразити у вигляді |
|
|
|
|
|
|
|
|
|
||||||||
W (i x ) A(x ) exp[i (x )] U (x ) iV (x ) , |
|
|
(23) |
||||||||||||||
де A(x ) називається амплітудо-частотною |
характеристикою |
||||||||||||||||
лінійної |
|
системи, |
а |
функція |
(x ) - |
|
фазово-частотною |
||||||||||
характеристикою лінійної системи. Відповідно до (19) та (23) ці характеристики будуть такими:
A( |
|
|
) |
ym |
(x ) |
[U |
2 |
( |
|
|
V |
2 |
( |
|
1/ 2 |
|
|
|||
x |
|
|
|
|
x |
) |
|
x |
)] |
, |
(24) |
|||||||||
gm |
(x ) |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
( |
|
|
) arctg |
V (x ) |
. |
|
|
|
|
|
|
|
|
|
|
(25) |
||||
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
U (x ) |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Введення |
|
характеристики |
|
повністю визначає |
динамічні |
|||||||||||||||
властивості лінійної системи. Значення амплітудно-фазової частотної передаточної функції W (i x ) та функції ваги (x) дає можливість
знайти сигнал на виході лінійної системи по вхідному сигналу довільної форми, а не тільки гармонійному. Отримаємо цю
залежність, |
застосувавши |
до |
співвідношення |
(15) |
||
|
|
|
|
|
|
|
y(x) (x' )g(x x' )dx' |
перетворення Фур’є: |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(x) exp(i x x)dx |
|
[ (x' )g(x x' )dx' ]exp(i x x)dx. |
(26) |
|||
|
|
|
|
|
|
|
Права частина виразу (26) являє собою Фур’є-перетворення від |
||||||
згортки двох функцій (x) |
та |
g(x) . Згідно з властивостями такого |
||||
перетворення, воно буде дорівнювати добутку Фур’є-перетворенню цих функцій:
Y (i x ) W (i x )G(i x ) , |
(27) |
де:
- 16 -
Y (i x ) y(x) exp(i x x)dx,
G(i x ) g(x) exp(i x x)dx.
спектри Фур’є вихідного та вхідного сигналів.
W (i x ) (x) exp(i x x)dx.
(28)
(29)
спектр Фур’є функції ваги системи.
Отже, для негармонійного сигналу амплітудо-фазова частотна передаточна функція W (i x ) містить багато спектральних гармонік і являє собою Фур’є-перетворення від функції (x) . Щодо змісту рівняння (27) функція W (i x ) є лінійним фільтром, що пропускає
вхідні сигнали різних частот (спектральних гармонік) і тим самим характеризує динамічні властивості лінійної системи. Якщо знайдений
комплексний спектр Y (i x ) вихідного сигналу згідно з (27) та (28), то перехід до самого сигналу y(x) здійснюється на основі зворотнього Фур’є перетворення.
1.1.2. Сигнали з кількома змінними
При роботі ОЕС вхідні та вихідні сигнали дуже часто залежать від кількох незалежних параметрів. Дослідження динаміки таких лінійних систем здійснюється з допомогою функцій, уведених вище, але залежних від кількох змінних.
Нехай вхідний g та вихідний сигнали є функціями n незалежних змінних x1, x2 ,..., xn . Сукупність таких змінних позначимо вектором
x{x1, x2 ,..., xn}. Відповідні сигнали запишуться у вигляді:
g g(x1, x2 ,...,xn ) g( X ) . (30)
y y(x1, x2 ,...,xn ) y( X )
Уведемо n - вимірну -функцію:
- 17 -
|
|
|
|
|
|
|
|
|
|
|
(x1 x10 |
, x2 x20 |
|
xn0 ); |
|
|
|
|
|
|
при |
|
x |
x0 |
, |
|
,..., xn |
(31) |
|||||
(x |
x0 ) |
|
|
|
|
|
|
|
|
(x1 x10 |
, x2 x20 |
,..., xn |
xn0 ). |
|||
|
|
|
|
|
0 |
при |
|
x |
x0 |
, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(32) |
|
|
... (x1 x10 , x2 x20 ,..., xn |
xn0 )dx1dx2 ...dxn 1; |
|||||||||||||
(x |
x0 )dx |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
(x) |
(x |
x0 )dx |
(x0 ); |
|
|
|
|
|
|
(33) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a1x1, a2 x2 ,..., an xn ) |
|
|
1 |
|
|
(x1, x2 ,..., xn ). |
|
|
(34) |
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
a1a2 ...an |
|
|
|
|
||||
Будемо враховувати, що при поданні на вхід лінійної системи |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сигналу g(x) |
(x |
x0 ) |
|
відгук |
системи |
(сигнал |
на |
виході) |
буде |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(x) |
(x) (x1, x2 ,..., xn ) . |
|
Функція |
(x) |
називається |
п- |
||||||||||
вимірною функцією ваги лінійної системи.
Сигнал на виході такої системи визначається через вхідний сигнал та функцією ваги п-вимірним інтегралом згортки:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y(x) |
(x |
' )g(x |
x |
' )dx |
' |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
|
|
|
(35) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
||||||||||
(x1' |
, x2' ,..., xn' |
) g(x1 |
x1' |
, x2 |
x2' |
,..., xn |
xn' )dx1' dx2' ...dxn' ; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n
Частотний зв'язок між п-вимірними спектрами вихідного Y (i x )
та вхідного G(i x ) сигналів визначається виразом:
|
|
|
|
Y (i x ) W (i x )G(i x ), |
(36) |
||
де x - п-вимірна кругова частота, що вводиться при використанні п-
вимірного перетворення Фур’є. Нехай задана функція f (x) . ЇЇ п- вимірний спектр визначається п-вимірним інтегралом Фур’є:
- 18 -
|
|
|
|
|
|
|
F (i x ) F (i x1 , i x2 ,..., i xn ) |
f (x) exp[ i x x]dx |
|
||||
|
|
|
|
|
|
(37) |
|
|
(n) |
|
|
|
|
|
|
|
|
|
|
|
... |
f (x1 , x2 ,..., xn ) exp[ i( x1 x1 , x2 |
x2 ,..., xn xn )]dx1dx2 ...dxn ; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n
Відповідно до (37), спектри вхідного та вихідного сигналів визначаються так:
|
|
|
|
|
|
G(i x ) |
g(x) exp(i x x)dx; |
(38) |
|||
|
|
|
|
|
|
|
(n) |
|
|
|
|
|
|
|
|
|
|
Y (i x ) |
y(x) exp(i x x)dx. |
(39) |
|||
(n)
При цьому п-вимірна амплітудо-фазова частотна передаточна функція визначається через функцію ваги:
W (i x )
|
|
|
|
|
(x) exp(i x x)dx. |
(40) |
|||
(n)
1.2.Перетворення Фур’є та його основні властивості
Ваналізі та синтезі ОЕС важливе місце посідає математичний апарат перетворення Фур’є. За допомогою такого апарату порівняно легко роз’язуються задачі спектрального аналізу динаміки лінійних систем, при цьому вдасться перейти від схожих інтегральних рівнянь до системи алгебраїчних рівнянь.
1.2.1.Спектри періодичних сигналів
Вабсолютному розумінні періодичних сигналів не існує, оскільки потреб не буде повторення одного і того ж процесу нескінчену кількість разів. Однак поняття періодичного сигналу дуже корисне в розгляді реальних процесів, що займають кінцеві інтервали часу та простору. Тут доцільно згадати роботу дифракційної гратки, випромінювання атомом квазімонохроматичного цугу хвиль і т.д.
-19 -

А) найпростішим періодичним сигналом є гармонійні коливання, що визначаються тригонометричними функціями косинуса та синуса часу чи простору:
(t) Acos[(2 / T )t ] |
|
|
|
|
|
|
|
|
|
||
Acos(t ) Acos |
|
при |
t |
||||||||
чи |
|
|
|
|
|
|
|
|
|
|
|
(x) Acos[(2 / )x ] |
|
|
|
|
|
|
|
|
|
||
Acos(x x ) Acos |
|
при |
|
x . |
|||||||
Тут |
A , T - період коливань, |
|
|
2 |
|
- кругова частота, |
1 |
- |
|||
t |
T |
|
|
||||||||
|
|
|
|
|
|
|
|
T |
|||
|
|
|
|
|
|
|
|
|
|||
частота, |
- довжина хвилі, |
|
|
2 |
|
- кругова просторова частота, |
|||||
x |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
f1 - просторова частота; , - початкова та повна фази.
Графічно ці коливання зображені на рис. 10.
Гармонічне коливання можна розглядати у вигляді дійсної частини (або уявної, в різних джерелах береться або дійсна, або уявна) комплексної змінної
(t) Re k (t) A Re ei A Re[cos i sin ] Acos , t .
Комплексне представлення допускає таку інтерпретацію: комплексний вектор k (t) обертається в комплексній площині з
кутовою частотою . Якщо за годинниковою стрілкою – знак «-», якщо проти – знак «+».
Модуль вектора k A . Проекцією k (t) на дійсну вісь і є сама функція (t) .
- 20 -
