Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черновицкий национальный университет им. Ю. Федьковича

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

FOKOEP_-_CHastina_1

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

1.88 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

називаються прямими перетвореннями Фур’є, а самі функції F (i x ) , F (if x ) - спектральною густиною, спектральною характеристикою, комплексним спектром Фур’є функції (x) .

Вирази

(x) 2 F (i x )ei x x d x ;

		(57)
		(57)

	(x) F (if x )ei 2 f x x df x .

називаються зворотними перетвореннями Фур’є.

При використанні шкали кругових просторових частот і введенні


позначень	lim	An X	F (i x ) , множник	1	з’являться у виразі для
		4		2

прямого перетворення Фур’є. У книзі М.М. Мірошникова «Теоретичні основи оптико електронних пристроїв» робиться висновок, що «тільки

	2
	2
так буде правильно: (x)	1	F (i		)ei x x d		й інші автори
так буде правильно: (x)		F (i	x	)ei x x d	x	й інші автори
			x		x

роблять помилку». Проте ніякої помилки тут немає: непорозуміння виникає через масштаб задання функції.

Звернемо увагу на розмірність функцій				F (i x ) та (x) . Якщо
розмірність			(x) - В, то, згідно з (57),	розмірність F (i x ) -
B[x]	B		. Із вигляду прямого Фур’є-перетворення Re[F(i x )] -

	[x 1
		]

завжди парна функція, Im[F(i x )] - непарна (рис. 17).

- 31 -

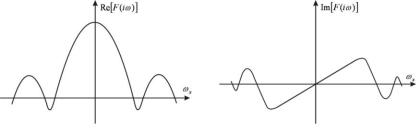
Рис. 17. Re[F(i x )] - завжди парна функція, Im[F(i x )] - непарна

Якщо (x) - парна функція, то (x) (x) , тоді F (i x ) -

парна, дійсна функція.

F (i x ) 2 (x) cos x xdx .

Якщо (x) - непарна функція, тобто (x) (x) , то


F (i x ) (x) cos x xdx i (x) sin x xdx


i (x) sin x xdx i2 (x) sin x xdx
	0

- суто комплексна непарна функція, а Im[F (i x )] 2 (x)sin x xdx .

Для функції залежної від п-аргументів, пара перетворень Фур’є

визначається згідно формул:

(x)

F (i

)ei x x d

;

(2 )n

(58)

F (i x ) (x)e i x x dx.

x2 ... x

Тут

x x x

xn -

скалярний добуток

п-

{x1 , x2 ,..., xn } та

вимірних

веторів

просторі координат

- 32 -

					{x	,x	,...,x	};		dx1dx2 ...dxn ;
просторі		частот		x	{x	,x	,...,x	};	dx	dx1dx2 ...dxn ;
					1	2		n
	d x	d x	...d x
d x	d x	d x	...d x	- елементарні об’єми у використовуваних п-
	1		2	n

вимірних просторах.

1.3.Властивості спектрів

1.3.1.Теорема про спектр суми

Нехай функції 1 (x) та 2 (x) мають спектри F1 (i x ) та F2 (i x ) . Унаслідок лінійності перетворення Фур’є отримаємо, що спектр суми двох функцій дорівнює сумі спектрів цих функцій:


F (i x ) F1 (i x ) F2 (i x ) [1 (x) 2 (x)]e i x x dx.	(59)

1.3.2. Теорема про парність і непарність функцій

Коли функція (x) - парна функція (тобто (x) (x) ), то парною буде також її спектральна густина:


F (i x ) (x)e i x x dx (x) cos x xdx ,

F(i x ) F(i x ) F(x ) - тільки дійсна функція.
Якщо функція	(x) - непарна (тобто (x) (x) ),		то її
спектральна густина також непарна та суто уявна:

F (i x ) (x)e i x x dx i (x)sin x xdx .		При	цьому

F(i x ) F(x ) .
1.3.3. Теорема про комплексно спряжене
Нехай (x) -	комплексний сигнал, F (i x )	- його спектральна

густина. Визначимо спектральну густину сигналу, що спряжений із(x) , тобто (x) .

Маємо:

- 33 -

(x) (x) i m (x),
(x)	(x) i	m	(x).

Позначимо	через		Fc (i x )	шукану спектральну густину
спряженого сигналу.

Fc (i x )	(x)e i x x dx (x)e i x x dx i m (x)e i x x dx

Проте

F (i x )

Відповідно

(x)e i x x dx i m (x)e i x x dx .

F (i x )

(x)ei x x dx i m (x)ei x x dx .

Порівнюючи Fc (i x ) та F (i x ) , бачимо: спектральна густина сигналу, комплексно спряжена із заданими, визначається шляхом заміни знака в аргументі та спряження, тобто Fc (i x ) = F (i x ) .

1.3.4.Теореми зміщення та запізнення

Упрактиці дуже часто доводиться зміщувати шкали частот, часу на постійну величину. Теорема зміщення встановлює зв’язок між

функціями зі зміщеними шкалами. Нехай F (i x ) - спектральна густина функції (x) . У загальному випадку (x) - комплексна

величина (використані позначення Порфир’єва).

(x) (x) ei arg ( x) .

Змістимо частоту x на величину x0 . Отримаємо спектральну густину F(i x x0 ) . Визначимо сигнал см (x) , що відповідає спектральній густині. Зі зворотного перетворення Фур’є отримаємо:

(x) 1 F[(i )]ei x x d .

см 2 x x0 x

- 34 -

Домножимо останній вираз на e i x 0 x ,

ei x 0 x , вводячи нову змінну

, отримаємо:

(x)

F[(i ' )]ei x' x d ' x ei x 0 .

см

На основі останньої рівності отримаємо:

(x) (x)ei x 0 x

(x)

см

i[ x 0 x arg ( x)]

(60)

Зміщення

спектральної густини

на x0

приводить до

модульованого сигналу з несучою частотою 0 x . Якщо уявити, що(x) - керуючий сигнал, то сигнал см (x) виявляється модульованим за амплітудою та фазою.

Змістимо сигнал (x) по часу на x0 . Це	зумовить нову
спектральну густини

Fсм (i x ) (x x0 )e i x x dx e i x x0 F (i x ) .	(61)

якщо ввести заміну x' x x .
0

Вираз (61) називають теоремою запізнення. При зміщенні функції (сигналу) в часі відбувається модуляція спектральної потужності.

Оскільки модуль нової функції Fсм (i x ) не змінюється, то ширина

спектра зміщеної та незміщеної функції однакова.
Змінюється	тільки	аргумент	спектральної	потужності,

Fсм (i x ) F(i x ) . А Fсм (i x ) arg F(i x ) x x0 .

1.3.5. Зв’язок між скалярним добутком функцій та їх спектрами. Рівність Парсеваля

Важливі співвідношення для функцій, що задовольняють перетворенням Фур’є, випливають з формули, вперше отриманої Релеєм.

Нехай 1 (x) та 2 (x) - дійсні чи комплексні сигнали та F1 (i x ) , F2 (i x ) - відповідні їм спектральні густини.

- 35 -

Скалярний добуток функцій 1																																і 2 , F1 і F2 визначається такими
рівностями:

(1 2 )									1 (x) 2 (x)dx ,																			(F1 F2 )									F1 (i x )F2 (i x )d x .

Формула Релея встановлює такий зв’язок між скалярним добутком
функцій та їх спектрів:
																	1
	(x)							(x)dx									1					F (i )F													(i )d													(62)
	(x)							(x)dx								2						F (i )F													(i )d													(62)
	1						2									2								1					x				2			x					x
	1						2																	1					x				2			x					x

або
(				)					1				(F F ) .
(			2	)									(F F ) .
	1		2						2						1				2
									2
Доведення (62):
(x)						1				F (i )ei x x d , (x)																												1		F (i )ei x x d .
(x)						2				F (i )ei x x d , (x)																											2			F (i )ei x x d .
1						2								1			x											x				2					2					2	x		x
1														1			x											x				2										2	x		x

Згідно з визначенням,
													1
(				)													F (i								)e i x x d												(x)dx.
(			2	)													F (i						x		)e i x x d												(x)dx.
	1		2								2								1				x												x 2
											2
Змінюючи порядок інтегрування отримаємо:
									2
									2
(				)					1						F		(i				)				e i x x d										dxd
(			2	)											F		(i			x	)				e i x x d										dxd				x
	1		2												1					x														x					x

	1	F							(i					)F (i							)d									1				(F F ).
		F							(i				x	)F (i						x	)d						x							(F F ).
	2					1							x		2					x							x			2					1				2
	2																													2

При 1 (x) = 2 (x) = (x) отримаємо																																						рівність,					що	називається
формулою Парсеваля:
	(x)				2 dx								1					F (i )								2 d .
													1																																			(63)
												2																																				(63)
												2										x									x

Ця рівність											виражає										закон збереження																			енергії. Якщо						(x)					2
Ця рівність											виражає										закон збереження																			енергії. Якщо						(x)					2
виражає			густину енергії																		на							одиничний											інтервал				х,		F (i		x	)	2	-
виражає			густину енергії																		на							одиничний											інтервал				х,		F (i			)	2	-

- 36 -

відповідно енергію, що припадає на одиничний інтервал шкали x , то

повна енергія, згідно з (63), при переході від однієї шкали до іншої, повинна зберігатись однією і тією ж. Зауважимо, що при використанні

шкали частот, множник 2 у виразах (62), (63) відсутній.

1.3.6. Скалярний добуток функцій зі зміщеними шкалами

Якщо у функцій 1				та 2	шкали зміщені на величину , то їх
скалярний добуток буде називатись функцією взаємної кореляції
функцій 1 і 2 :

K12 ( ) 1 (x) 2 (x )dx .								(64)

На основі формули Релея і теореми зміщення отримаємо
K ( )	1	F (i )F			(i )ei x d .			(65)
K ( )	2	F (i )F			(i )ei x d .			(65)
12	2		1	x 2		x	x
12			1	x 2		x	x

З останньої рівності випливає, що функція взаємної кореляції K12 ( ) являє собою зворотне перетворення Фур’є від добутку функції

F1 (i x ) F1 (i x ) .

Якщо 1 (x) 2 (x) (x) , то функцію (66) називають функцією автокореляції:

2 ei x d

K ( )

(x) (x )dx

F (i

)

(66)

Функції

K12 ( ) та K ( )

посідають важливе

місце

в теорії

когерентності, аналізі шумів ОЕС, Фур’є-спектроскопії та взагалі при вивченні різноманітних випадкових процесів.

- 37 -

1.3.7. Згортка функцій

Згорткою функцій 1 (x)

та

2 (x)

називається інтеграл вигляду

1 (x x' ) 2 (x' )dx' . Згортка позначається так: 1 2 . Для згортки

характерна комутативність 1 2

2 1 .

Доведемо таку теорему: спектральна густина згортки функцій 1

та 2

дорівнює добутку їх спектральних густин, тобто:

(x)

1 (x x' ) 2

(x' )dx'

F1 (i x )F2

(i x )ei x x d x

(67)

Доведення (67) випливає із формули Релея та властивостей Фур’є-

перетворення.

Функція

(x' ) має

спектральну

густину

F (i

) . Функція

(x' ) повинна мати

спектральну

густину

) . Візьмемо

функцію

(x'

) , для якої спектральна густина на сонові

теореми про запізнення буде F (i

)e i x x .

Згідно з формулою Релея, скалярний добуток функцій

(x' ) та

(x'

) буде дорівнювати:

(x'

) (x' )dx'

[F (i )e i x x ]F (i )d

або остаточно

(x x' ) (x' )dx'

F (i )F (i )ei x x d .

Знайдемо Фур’є-перетворення від згортки:

(x) 1 (x' ) 2 (x x' )dx' ,

- 38 -


F (i x ) (x)e i x x dx 1 (x' )dx' 2 (x x' )e i x x dx .

Уводячи змінну y x x' , маємо:

' ' i x x'		i x y		(67а)
F (i x ) 1 (x )dx e	2 ( y)e		dy F1 (i x )F2 (i x )	(67а)
F (i x ) 1 (x )dx e	2 ( y)e		dy F1 (i x )F2 (i x )

Відповідно Фур’є-перетворення згортки двох функцій дорівнює добутку їх спектральних густин:

1 2 F1 F2 .

Якщо функції 1 (x) та 2 (x) дійсні, парні, то відповідно до

властивостей парності функцій, що задовольняють Фур’є- перетворенням, будемо мати:

(x x' )

(x' )dx'

F (i

) cos

1 x

Із визначення згортки слідує також наступна властивість: спектральна густина F(i x ) відповідає Фур’є перетворенню від

добутку сигналів 1 (x) 2 (x) , тобто:

F (i x )

1 (x) 2 (x)e i x x dx , то

F (i )

F [i(

' )]F

(i ' )]d '.

(68)

Формула Релея:

(x)

(x)dx

F (i )F (i )d .

3 x

Позначимо

(x)

(x)e i x' x .

Функції 3 (x) відповідає спектральна густина

F3 (i x ) , функції

2 (x) - спектральна густина F2

(i x ) .

- 39 -

Спектральна густина сигналу 3 (x) буде F3 (i x ) , а сигналу

2 (x)e i x' x відповідно до теореми запізнення - F2 (i x i x ' ) .

Маємо:

F3 (i x ) F2 (i x i x ' ) F3 (i x ) F2 (i x i x ' ) .

Підставляючи значення 3 (x) , F3 (i x ) у формулу Релея, отримаємо:

				1
(x) (x)e i x'			x dx		F (i )F [i('		)]d ,
				2
	1	2			1 x 2	x	x	x

що відповідає (68) при перепозначенні x' x , x x' .

Вираз (68) свідчить про те, що спектральна густина добутку двох функцій дорівнює згортці їх спектральних густин, поділеній на 2 , тобто

F (i x ) 21 F1 F2 .

1.3.8. Теорема про спектр похідної

Нехай спектр функції (x)				дорівнює F(i x ) . Визначимо спектр
F1 (i x ) , що відповідає				похідній від заданого сигналу
' (x)	d (x)	. Згідно із Фур’є-перетворенням маємо:
' (x)		. Згідно із Фур’є-перетворенням маємо:
	dx

F1 (i x ) ' (x)e i x x dx				e i x x d (x).

		b			b
Інтегруючи частинами udv uv					ba vdu , знайдемо


		a			a

F1 (i x ) (x)e i x x			(x)(i x )e i x x dx.

- 40 -

<<< < Предыдущая 1 2 34 / 104 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.02.2016116.22 Кб12Fin_zv_1_1.doc
#
22.08.2019230.12 Кб26fitopatologiya.docx
#
14.09.2019281.86 Кб6Fizika(1).docx
#
08.11.2018285.18 Кб19fizika7_9.doc
#
28.09.201974.75 Кб3Fizyka_mag.doc
#
23.02.20161.88 Mб7FOKOEP_-_CHastina_1.pdf
#
23.02.20161.86 Mб8FOKOEP_-_CHastina_2.pdf
#
22.11.2019462.55 Кб3Fondovy_rinok_metodichka (1).docx
#
02.09.20191.13 Mб34Fotocon_SC.doc
#
23.02.2016468.01 Кб14Fotogrammetriya моє.rtf
#
23.02.201656.32 Кб29FOTOMETRIYa2014.doc