19.10. Воднеподібні атоми

До воднеподібних атомів відносяться власне водень та група одновалентних лужних елементів, однократно іонізований атом гелію , двічі іонізований атом літіюі т.п. Потенціальна енергія електрона у таких атомах у полі ядра із зарядом Ze записується у вигляді

,

де r  відстань електрона від ядра. При цьому рівняння Шредінгера запишеться так

. (1)

Зважаючи на сферичну симетрію воднеподібних атомів, вводяться сферична система координат і в ній рівняння Шредінгера записується у виді

. (2)

Не приводячи у явному вигляді вираз лапласіана у сферичній системі координат, вкажемо, що розв’язок рівняння (2) знаходиться у вигляді

(3)

В (3)  радіальна хвильова функція,  сферична хвильова функція. Числа n,l,m мають назву квантових чисел:

• n=1,2,3,…  головне квантове число, що визначає енергію електрона у атомі та ймовірність знаходження електрона на відстані r від ядра. Усі електрони атома з однаковим головним квантовим числом формують його енергетичну оболонку.

• l=0,1,2,…,n-1 – азимутальне (орбітальне) квантове число, що визначає момент імпульсу електрона у атомі. Азимутальне квантове число формує підоболонку електронів з однаковим моментом імпульсу.

• m=0,  1,  2, ... ,  l – магнітне квантове число, що визначає проекцію моменту імпульсу на вісь , яку ототожнюють із напрямком вектора магнітної індукціїзовнішнього електромагнітного поля.

а). Власні значення енергії. Власне значення енергії електрона в полі ядра дискретне і має вигляд

, (1)

а для електрона не зв’язаного з ядром енергія Е>0 і неперервна. Найменша величина енергії водню буде при n=1 і

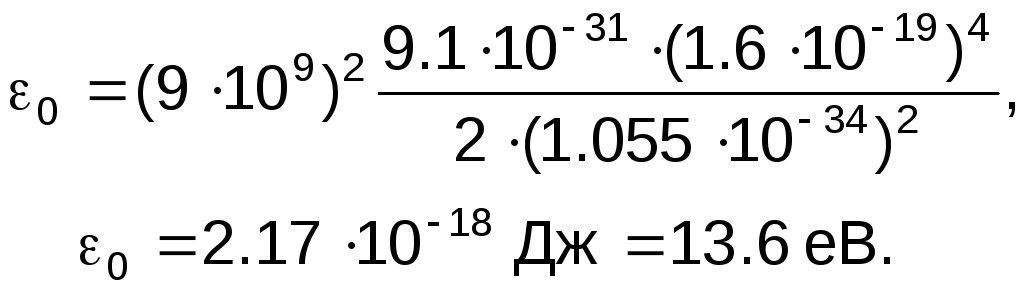(2)

Використовуючи (2) можна записати

. (3)

Число N можливих станів у межах енергетичної оболонки визначається сумою N_m по всім можливим значенням l

(4)

і знаходиться як сума n членів арифметичної прогресії з різницею d=3, першим членом а₁=1 та n-м членом а_n=2n-1

.

Усі можливі стани атома водню класифікуються умовними позначеннями через позначення енергетичних оболонок n та їх підоболонок l за схемою, поданою в таблиці. Випромінювання та поглинання світла атомом відбувається з певними обмеженнями, які ще називають правилами відбору.

Номер оболонки	Підоболонкичисло станів з урахуванням значення спіна				число станів в оболонці
n	l=1	l=2	l=3	l=4
1	1s2				2
2	2s2	2p6			8
3	3s2	3p6	3d10		18
4	4s2	4p5	4d10	4f14	32

Виявляється, що при переходах електрона між енергетичними рівнями, у першому наближенні, повинно відбуватися таке обмеження на азимутальне квантове число l

l=1, (5)

яке пов’язане із законом збереження імпульсу, коли враховані імпульси атома й фотона, що випромінюється чи поглинається. Таким чином в атомі можливі переходи

nsmp, npmd і т.п.

б). Власні функції. Власні функції є добутком двох множників. Множникє розвязком радіальної частини рівняння Шредінгера, ядром якого є функція Лагерра. Цей множник залежить від квантових чисел n, l. Сферична функція є розвязком частини рівняння Шредінгера, яка залежить від кутів і визначається квантовими числами l, m. Можна показати, що функціяє власною функцією квадрата моменту імпульсуі його проекції. Густина ймовірності знаходження електрона на відстані r від ядра задається виразомі для декількох функцій на малюнку 13 наведена відповідна її залежність від r у мірилі борівського радіуса. З малюнка видно, що найбільш імовірними є відстані від ядра, що співпадають із радіусами відповідних борівських орбіт.

Наведемо декілька значень радіальної та сферичної функцій, поклавши (див.Мал.199)

, ,

.

, ,,.

в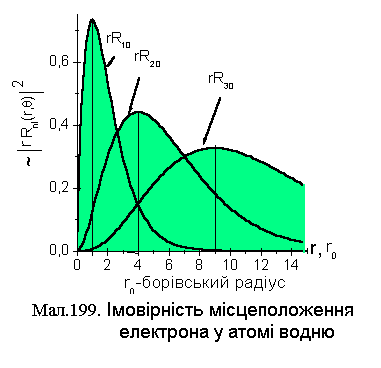). Принцип відповідності Бора. Розглянемо одну спільну властивість енергій електрона, що знаходиться у потенціальній ямі, електрона, що здійснює гармонічні коливання (осцилятор) та, на кінець, електрона у воднеподібному атомі. Знайдемо відносні проміжки енергій електронів для перелічених випадків.

1. Для частинки у глибокій потенціальній ямі для енергії справджуються такі співвідношення

,,.

2. Для гармонічного осцилятора можна записати

,,

3. Для воднеподібних атомів. У випадку n+1-го енергетичного рівня маємо

,

а відносний проміжок становитиме

.

В усіх перелічених випадках при великих числах n (n>>1) маємо й енергія стає неперервною. Це означає, що починаючи з деяких значень квантових чисел, енергія частинки може розглядатися як класична.

Одержаний результат є окремим випадком загального принципу відповідності Бора, який він установив в 1923 році стосовно квантової механіки. За цим принципом будь-яка нова, більш узагальнена теорія природних явищ у фізиці, що є розвитком класичної теорії, не відкидає останньої узагалі, а містить її у собі у певних межах застосування, причому у граничних випадках нова теорія переходить у попередню. Так, наприклад, при малих швидкостях тіл V<<c, релятивістська механіка переходить у класичну, а при квантова механіка переходить у класичну.