19.7. Гармонічний осцилятор

Г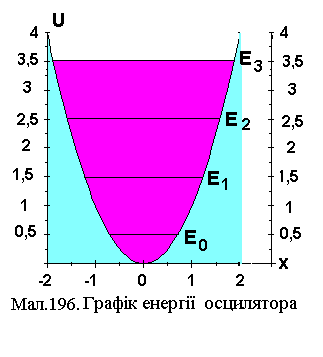армонічним осцилятором називають частинку, що здійснює гармонічні коливання під дією пружної сили, де k коефіцієнт пружності. Потенціальна енергія осцилятора (див.Мал.196), а власна частота, де m маса частинки, тобто

.

В одновимірному просторі стаціонарне рівняння Шредінгера для осцилятора можна записати у вигляді

.

Скінчений, однозначний і неперервний розв’язок цього рівняння існує при умові, що

.

Найменше значення енергії осцилятора, яке дорівнює , називають нульовою енергією осцилятора і вона визначає його енергію при температурі Т=0 К, тобто при Т=0 К частинки, що знаходяться у вузлах кристалічної решітки здійснюють нульові коливання. Результати дослідів по розсіюванню світла в кристалах при Т0 підтверджують цю тезу.

Принцип відповідності. В 1923 році Н.Бор установив принцип відповідності, що вимагає перехід наслідків квантової механіки в класичні при ћ0. Іншими словами в цьому випадку квантово-механічний опис явищ повинен співпадати з класичним. Зокрема, у граничному наближенні до великих квантових чисел квантовий опис також повинен співпадати з класичним.

19.8. Потенціальний бар’єр та його прозорість

Нехай вільна частинка рухається вздовж осі ОХ в напрямку скінченого потенціального бар’єра U=U₀ для 0хL і U=0 для (x<0, x>L) із енергією EU₀ (див.Мал.197 а) ). Її рух задається плоскою -хвилею. При падінні частинки на границю бар’єра, вона проникає в нього на деяку глибину х_е (глибина, на якій імовірність зменшується в е раз) і з певною ймовірністю може пройти через нього наскрізь або відбитися від нього навіть при Е>U₀. Для розв’язку цієї задачі з E<U₀ потрібно скористатися відповідними умовами неперервності -функції та її похідних на границях бар’єра. Відповідні розрахунки дають

.

Оцінка висоти проникнення електрона провідності над поверхнею металу показує, що при бар’єрі електрони виходять із метала на висоту x_e0.1 нм.

Для прямокутного бар’єра ймовірність D того, що частинка опиниться за бар’єром може бути представлена наближеним виразом

.

Д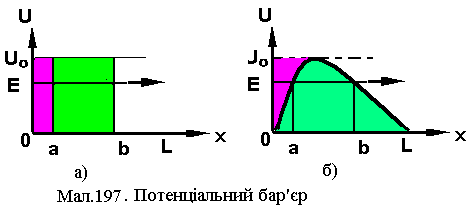ля бар’єра довільної форми (див.Мал.197 б) )

.

При подоланні потенціального бар’єра частинка начебто проходить через "тунель". Саме тому явище проходження частинкою бар’єра називають тунельним ефектом. Тунельний ефект дозволив пояснити цілий ряд фізичних явищ, які не мали пояснення з класичної точки зору. Зокрема, явище автоемісії, яке полягає в тому, що під дією сильного електричного поля, створеного при поверхні металу, спостерігається виліт електронів із металу. Таке поле перетворює потенціальний бар’єр на поверхні провідника в скінчений. В результаті стає можливим тунелювання електронів за поверхню металу.

19.9. Квантування моменту імпульсу

Існує чотири квантові оператори, за допомогою яких визначається момент імпульсу частинки: оператор квадрата моменту імпульсу , та три оператори проекцій імпульсу . Згідно принципу невизначеностей, одночасно можуть бути визначені лише квадрат моменту та одна з його проекцій. Розв’язок операторного рівняння

має результатом власне значення

,

де l=0,1,2,... азимутальне квантове число й модуль моменту імпульсу квантується

.

У сферичній системі координат (r,,)

і відповідне рівняння

.

Підстановкою =e^ одержимо

і,

а розв’язком буде .

Умовою однозначності розв’язку є

(+2)=(),

тобто

.

Ця умова виконується якщо покласти , де m=0,­­1,2,3,... магнітне квантове число. Проекція не може бути більша величини вектора, тобто L>L_z і , тобто найбільше значення m дорівнює l: m=0,­­1,2,3,...l.

Момент імпульсу системи частинок дорівнює сумі моментів цих частинок, яка також квантується і записується у вигляді , де L азимутальне квантове число системи частинок. Найбільше значення L буде коли моменти мають один напрямок і найменше при протилежних напрямках моментів частинок. Наприклад, якщо система складається з двох частинок, то L=l₁+l₂, l₁+l₂-1, ... ,| l₁-l₂|.