19.4. Суперпозиція станів у квантовій механіці

У квантовій механіці кожній фізичній величині зіставляється оператор , який описує сукупність математичних операцій, за якими можна обчислити його власне значення та відповідну власну-функцію. У стаціонарному рівнянні Шредінгера можна визначити енергетичний оператор, власними значеннями якого є енергія частинки Е. Такий оператор називається оператором Гамільтона і він має вид

. (1)

Оператор Гамільтона приписує, що для знаходження повної енергії частинки, потрібно скласти диференціальне рівняння

(2)

і розв’язати його, знайшовши Е і . Узагалі для будь-якого оператора складається диференціальне рівняння

, (3)

яке розв’язується при відповідних крайових умовах. Розв'язок дає власні значення q₁,q₂,q₃...q_n... та власні функції ₁,₂,₃..._n.... Вимірювання величини q можуть показати, що вона завжди має певне значення, а може статися, що в різних вимірюваннях будуть різні значення q. У першому випадку кажуть, що q має певне значення, а у другому випадку  величина q із різною ймовірністю приймає відповідні значення зі свого спектра, а  -функція такого стану може бути записана у вигляді суперпозиції власних функцій

, (4)

причому, функції є ортонормованими

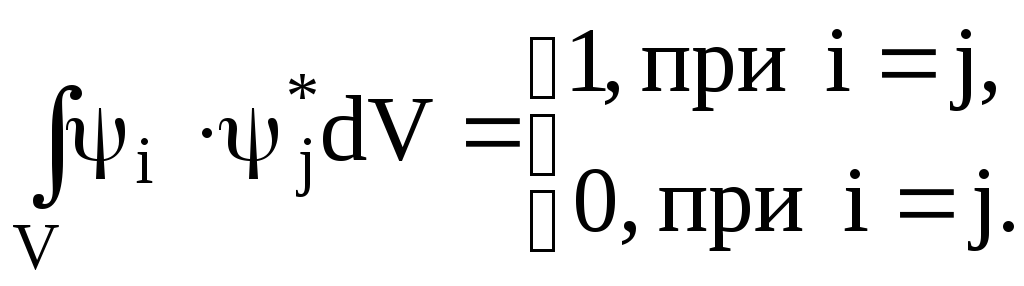
Тепер можна записати

. (5)

Квадрат модуля визначає ймовірність того, що при вимірюванні буде одержане значення власної величини q=q_і.

19.5. Рух вільної частинки

Рух вільної частинки характеризується сталою швидкістю V, а повна енергія Е є кінетичною енергією. Направимо вісь Ох уздовж напрямку руху. Стаціонарне рівняння Шредінгера тепер матиме вигляд

, (1)

де  хвильове число. Розв’язком цього рівняння є хвильова функція

. (2)

Повним розв’язком рівняння Шредінгера буде

, (3)

де . Таким чином рух вільної частинки у квантовій механіці описується плоскою монохроматичною хвилею. При розповсюдженні частинки в напрямкові Ох

,

а величина ||²=|A|² не залежить від часу t.

19.6. Частинка у нескінченно глибокій потенціальній ямі

Нехай електрон знаходиться в одновимірній потенціальній ямі шириною L із потенціальною енергією U=0 для 0<x<L і U= для (x0, xL), причому граничні умови для -функції зводяться до =0 при x0 і xL. Стаціонарне рівняння Шредінгера для електрона в ямі буде мати вигляд рівняння для вільного електрона

, (2)

де хвильове число. Розв’язком цього рівняння є хвильова функція

=Asіn(kx+). (3)

Знайдемо сталі A та  із граничних умов. З умови

(x=0)=Asіn=0 (4)

слідує

=0,

а з умови

(x=L)=Asіn(kL)=0

слідує

k_nL=n

. (5)

Останній вираз означає, що на ширині ями L повинно вкладатися ціле число півхвиль де Бройля. Основним висновком із розв’язку даної задачі є те, що обмеження руху електрона у просторі призводить до виникнення дискретності його енергії. Із слідує, що

. (6)

Крок дискретності енергії для електрона дорівнює

(7)

Для електрона в ямі з L=10^-9 м Е_n=0.377 еВ, а для макроскопічної ями з L=10^-2 м=1 см маємо Е_n=3.7710^-15 еВ і спектр енергій квазінеперервний. Розподіл імовірності знаходження частинки в ямі задається виразом y=, а максимуми її для кожного з n знаходяться в точках, де m=1,2,...,n-1. В той же час із класичної точки зору знаходження частинки в кожній точці простору ями рівно ймовірне.

З умови нормування

(8)

знайдемо

.

Остаточно розв’язок має вигляд

. (9)

Густина імовірності знаходження електрона в точці х пропорційна і вона вона представлена на графіку Мал.195.

Покажемо, що функції є ортонормованими, тобто задовольняють співвідношенням

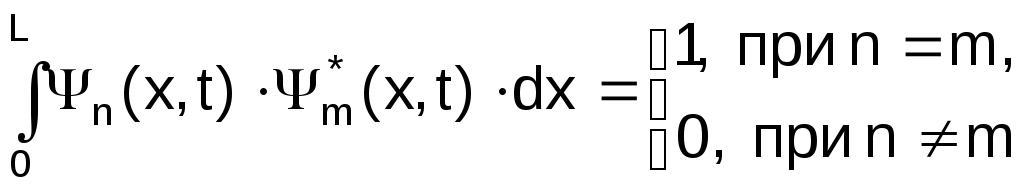, (10)

де функція є комплексно спряженою до функції.

Д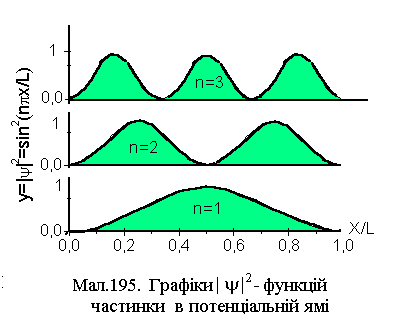оведемо (1) у явному виді. Підставимо у (1) значення функцій і проведемо очевидні перетворення.

При

Тепер

. (11)

При n=m

,

,.

Тепер

. (12)

Вирази (11-12) доводять співвідношення ортонормованості -функцій (10).