19.2. Хвильова -функція Луї де Бройля та її фізичний зміст

Наявність хвильових властивостей у частинок, що рухаються ставить питання про фізичний зміст їх хвильових функцій, які було названо . Для характеристики хвиль де Бройля знайдемо спочатку фазовута груповушвидкості такого хвильового процесу, у якому частинка рухається із швидкістюV<c і має енергію W. Для знаходження фазової швидкості, запишемо послідовність очевидних рівностей, що випливають з формули Луї де Бройля

і . Для групової швидкості маємо

і

,,

тобто групова швидкість хвилі дорівнює швидкості частинки .

У дослідах по дифракції електронів у різних точках простору спостерігалось більше чи менше скупчення електронів, що відповідало різним значенням інтенсивності хвиль де Бройля. Це означає наявність певної ймовірності знаходження електрона в точках простору, яка характеризується густиною ймовірності і яка зв’язана з інтенсивністю хвиль де Бройля. В 1926 р М.Борн сформулював такий фізичний зміст хвиль де Бройля: квадрат модуля псі-функції визначає густину ймовірності dР того, що частинка знаходиться в елементі об’єму dV=dxdydz, обмеженого координатами x, x+dx;y, y+dy; z, z+dz,

.

За допомогою -функції можна обчислити середні значення величин, які характеризують стан частинки, наприклад, для середнього значення відстані електрона від ядра можна записати вираз

.

Псі-функція повинна бути нормованою

.

Нормованість псі-функції означає, що ймовірність знаходження частинки в наданому їй об'ємі V дорівнює 1.

19.3. Рівняння Шредінгера

У класичній механіці рівняння руху за другим законом Ньютона розв’язується основна задача механіки: за заданими силами, що діють на макроскопічне тіло, та початковими умовами для координат та швидкості, знаходяться координати й швидкість тіла в будь-який момент часу. Подібним рівнянням, у квантовій механіці є хвильове рівняння Шредінгера для , яке він одержав в 1926 році. Це рівняння, як і рівняння руху Ньютона, не виводиться, а постулюється. Хвильове рівняння Шредінгера

(1)

визначає хвильову функцію де Бройля через потенціальну енергію силового поля U(x,y,z,t), в якому знаходиться частинка. В цьому рівнянні m маса частинки,  уявна одиниця,

 оператор Лапласа. На -функцію накладаються такі умови:

а) вона має бути скінченою, однозначною та неперервною разом із своїми першою та другою похідними по x,y,z,t;

б) функція ||², яка має фізичний зміст імовірності, має бути інтегрованою, тобто такою, що інтеграл є скінченною величиною.

Записане хвильове рівняння Шредінгера, називається часовим: в ньому потенціальна енергії може залежати від часу t. Якщо потенціальна енергія не залежить від часу, то функцію можна шукати у вигляді

, (2)

де Е  повна енергія частинки. Дійсно, підстановка (2) у рівняння Шредінгера (1) приводить його до рівняння

, (3)

яке називається стаціонарним рівнянням Шредінгера, так як воно у явному виді не залежить від t.

Розв'язок рівнянь (1) та (3) означає, що через вираз для функції , ми визначаємо усі стани частинки, в яких вона може перебувати, знаходячись у потенціальному полі U(x,y,z,t).

Коротко зупинимось на властивостях рівняння Шредінгера

• хвильові функції повинні бути однозначними та неперервними в усьому просторі, навіть коли Потенціальна енергія буде мати поверхні розриву;

• частинка не може проникнути у ту область, де ;

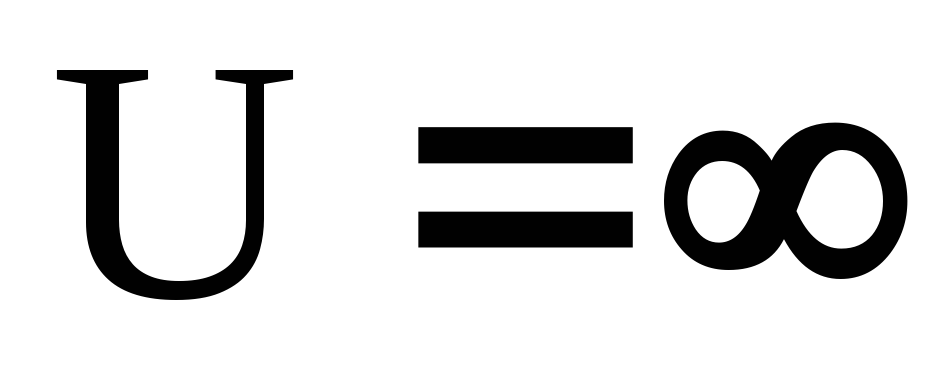• хвильові функції повинні бути скінченими, якщо U стає нескінченною;

• хвильові функції повинні мати неперервними першу та другу похідні;

• при від'ємному значенні потенціальної енергії U енергія частинки дискретна й від'ємна, а енергетичні рівні згущуються у напрямку до рівня з Е=0.