14.3.1.Дифракція на круглому отворі.

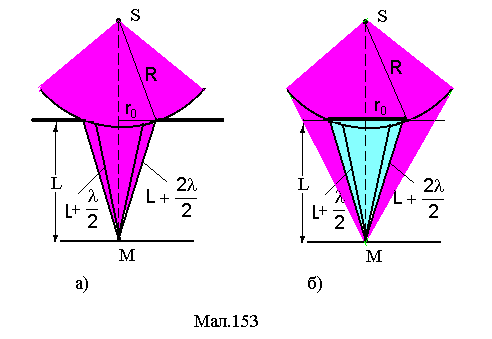
Амплітуда коливань при дифракції світла точкового джерела на круглому отворі (див.Мал.153а) радіуса r_o визначається сумою амплітуд від

(1)

перших відкритих зон Френеля. Для непарних m амплітуда результуючого коливання в точці М може бути представлена у виді

і в результаті одержимо

, (2)

що є максимумом освітлення. Для парних m одержимо

,

, (3)

що дає мінімум освітлення.

Результуючу амплітуду А можна значно збільшити за допомогою зонної пластинки Френеля. Це прозора скляна пластинка, на якій створені непрозорі покриття, що закривають всі парні зони Френеля і залишають відкритими всі непарні зони. Якщо число всіх зон Френеля, які вміщуються на пластинці N, то

, (4)

а інтенсивність (освітленість) у точці М при цьому буде в разів більшою, ніж без пластинки.

14.3.2.Дифракція на круглому дискові.

Амплітуда коливань при дифракції світла точкового джерела на круглому дискові (див.Мал.153б) радіуса r_o визначається номером першої відкритої зони

, (5)

а результуюча амплітуда дорівнює

. (6)

14.4. Дифракція Фраунгофера на плоскопаралельній щілині

Дифракція Фраунгофера  дифракція світла в паралельних променях. Нехай паралельний пучок променів світла падає нормально на непрозору площину BG, в якій прорізано плоскопаралельну щілину малої ширини b. Паралельно площині BG (див.Мал.154) розташовано збиральну лінзу Л та екран Е. Проведемо наближений розрахунок амплітуди коливань у точці екрана М, у якій лінзою збираються промені, що виходять із щілини під кутом до неї. За Гюйгенсом, точки щілини є вторинними джерелами світла. Щілину можна розбити на зони Френеля у вигляді смуг, паралельних ребру щілини В. Різниця ходу між променями, що виходять із країв зони ЗР, дорівнює , а тому ширина смуги(гіпотенуза ЗЗ) дорівнює . Результуюча амплітуда коливань, викликаних світлом від зон Френеля, є алгебраїчною сумою їх амплітуд, у яку амплітуди від сусідніх зон входять із протилежними знаками. Якщо число зон

(1)

парне (N =2m), то спостерігається мінімум дифракції, умовою якого є

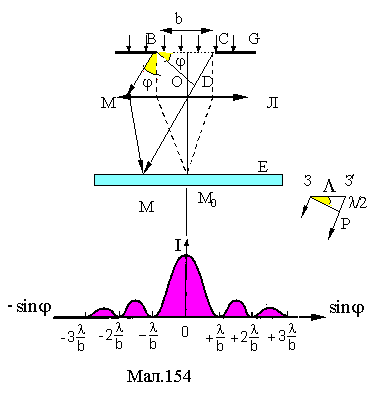(2)

Зауважимо, що величина

(3)

є різницею ходу променів, які йдуть від країв щілини.

Точний розрахунок інтерференції від щілини полягає у розбитті вторинного фронту випромінювання на нескінченно малі зони з нескінченно малим зсувом фаз, як це зроблено у п.13.8. Для нашого випадку потрібно зробити заміну

.

В результаті одержимо величину амплітуди в точці М

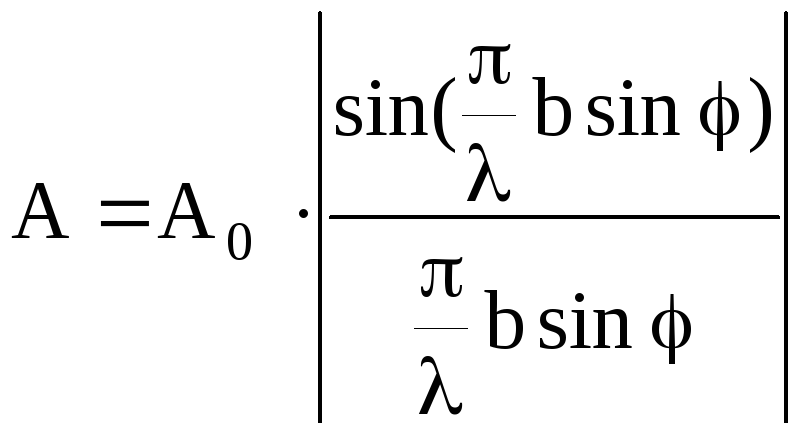. (4)

Розподіл інтенсивності в залежності від подано на малюнку.

14.5. Дифракція Фраунгофера на дифракційній решітці

а). Розподіл інтенсивності. Дифракційна решітка утворюється періодичною повторюваністю прозорих (шириною b) та непрозорих плоскопаралельних ділянок (шириною а) на прозорій (наприклад, скляній) поверхні BCG ( див.Мал.155). Величина

d = b + a (1)

називається періодом або сталою решітки. При освітленні решітки світлом, що падає нормально на її поверхню, в напрямку  відбувається інтерференція світла від усіх щілин, із сталою величиною зсуву фаз

, (2)

д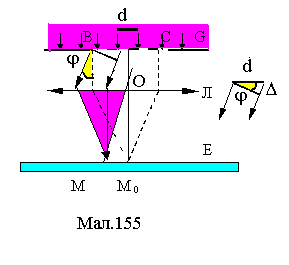е  різниця ходу між променями сусідніх прозорих щілин.

Процес інтерференції світла від багатьох прозорих щілин можна описати за допомогою багатопроменевої інтерференції, розглянутої у п.13.8. Результуючу амплітуду можна записати у вигляді

(3)

де  амплітуда хвилі, що утворюється дифракцією від окремої прозорої щілини в напрямку

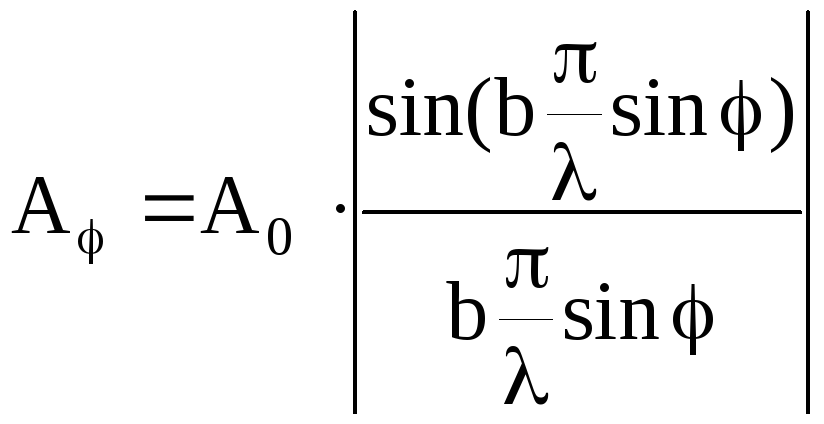. (4)

У цьому виразі А₀  амплітуда коливань у точці , при дифракції від однієї щілини у напрямку .

Максимуми виразу (3), що задаються умовою

. (5)

називаються головними. Амплітуда головного максимуму дорівнює

. (6)

В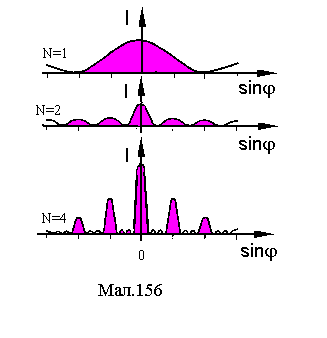еличинаn називається порядком головного максимуму. Головні мінімуми задаються виразом

(7)

Якщо з умови головного максимуму підставити

,

то вираз (3) для амплітуди головного максимуму n-го порядку запишеться у вигляді

. (8)

Головні максимуми розмежовані між собою мінімумами, які задаються умовою

. (9)

Таким чином між двома сусідніми головними максимумами знаходяться (N - 1) мінімум та (N - 2) додаткових максимуми.

На Мал.156 представлено розподіл головних максимумів при різних значеннях числа щілин N в решітці.

b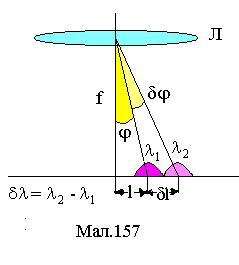). Дисперсія дифракційної решітки. Кутова дисперсія дифракційної решітки за визначенням є

, (10)

де  кутова відстань між максимумами одного порядку для двох ліній з (див.Мал.157). З умовидиференціюванням одержимо вираз. Звідси вираз (10) у вигляді

. (11)

Лінійна дисперсія дифракційної решітки за визначенням є

, (12)

де є лінійна відстань на екрані чи фотопластинці між максимумами одного порядку для двох ліній з. Величину, яка спирається на кутможна записати через фокусну відстаньf лінзи, яка зводить промені світла в одну точку

і після підстановки у вираз (12) одержимо

, (13)

тобто лінійна дисперсія представляється через кутову.

c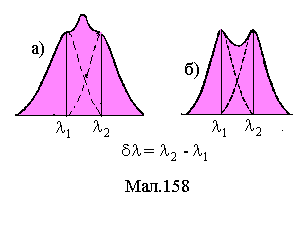). Роздільна здатність дифракційної решітки. Роздільна здатність дифракційної решітки за визначенням є

, (14)

де  найменша величина для заданої , при якій розрізнюються максимуми для довжин хвиль (див.Мал.158).

Величину R можна визначити через параметри решітки за допомогою критерію Релея: дві лінії у спектрі дифракційної решітки будуть розділені, якщо положенню максимуму n-го порядку для

буде відповідати перший мінімум біля максимуму n-го порядку для лінії з

.

З цього критерію випливає, що

. (15)

Тепер роздільна здатність запишеться у вгляді

R = nN. (16)