13.4. Видність інтерференційної картини

Величина

, (1)

де  максимальне та мінімальне значення інтенсивності в інтерференційних порядках, називається функцією видності. З експериментальних досліджень випливає, що око впевнено розрізнює смуги при V>0.1, тобто при . Користуючись виразом для інтенсивності інтерференції двох хвиль знаходимо

і тепер видність когерентного випромінювання має вид

. (2)

При видність максимальна (V = 1).

Частково когерентне випромінювання з інтенсивністю І можна розглядати як суму двох складових: когерентної з інтенсивністю та некогерентної з інтенсивністю. Результуючу інтенсивність можна записати так

.

Позначивши ступінь когерентності світла через , можна записати. При додаванні частково когерентних хвиль інтерференційну картину змазує некогерентна частина, яка створює рівномірно освітлений фон, причому

і

, (3)

тобто видимість частково когерентного випромінювання з інтенсивностями зменшується. Причому

. (4)

13.5. Інтерференція у тонкій плівці

Такого роду інтерференція спостерігається у сонячному випромінюванні відбитому від масляних плям, що розтікаються на воді. Товщина таких плям може бути надзвичайно малою та близькою до довжини хвиль світла. Описати таку інтерференцію можна у такий спосіб.

Тонка плівку можна представити у вигляді плоскопаралельної пластинки з показником заломлення світла n₂ та товщиною d. Інтерферують промінь 1', відбитий від верхньої поверхні плівки та промінь 2', відбитий від дна плівки і вийшовший з пластини в середовище з показником заломлення світла . На Мал.143 Л  лінза, що зводить промені в точці інтерференції.

Оптична різниця ходу між променями 1'та 2'дорівнює

, (1)

д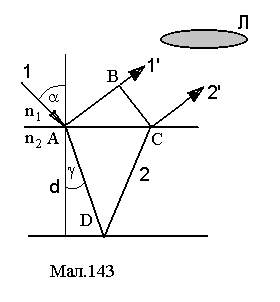е  кут падіння, доданок враховує, що промінь відбивається від дна плівки на границі, деі при цьому фаза хвилі змінюється на. Умова максимумів інтерференції

(2)

і мінімумів

. (3)

Вираз (1) можна одержати з таких міркувань. Закон заломлення світла дає

.

Оптичний шлях променя 2 у плівці

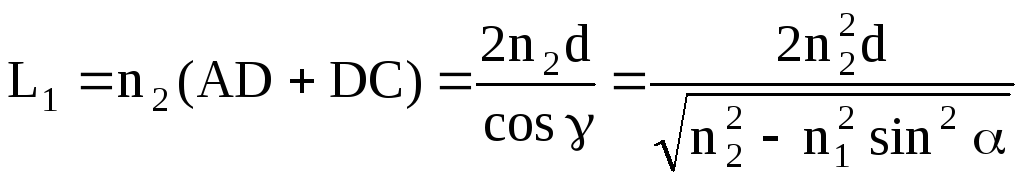(4)

Оптичний шлях променя 1 над плівкою

. (5)

Оптична різниця ходу 1 та 2 променів становить

.

Підставляючи у цей вираз (4) та (5), одержимо

. (6)

Якщо врахувати зміну фази променя 2 при відбитті від нижньої поверхні плівки на (різниця ходу), одержимо

, (7)

де довжина хвилі у середовищі плівки. Вираз (7) і є розв'язком задачі про оптичну різницю ходу.

13.6. Кільця Ньютона

Кільця Ньютона  інтерференційна картина, що спостерігається в оптичній схемі, представленій на Мал.144. Плосковипукла лінза з достатньо великим радіусом кривизни R повернена випуклою поверхнею до плоскої пластинки П і дотикається до неї у точці О.

Паралельний пучок світла падає нормально на плоску поверхню лінзи і частково відбивається від верхньої та нижньої поверхонь повітряного простору між пластинкою та лінзою. При накладанні відбитих хвиль виникають інтерференційні кільця, які відповідають певним радіусам, що визначають різницю ходу променів. З наведеного малюнку видно, що

,

а оптична різниця ходу

.

Доданок пов'язаний із зсувом за фазою на  при відбиванні світла від поверхні пластинки, яка оптично щільніша за повітря. У відбитому світлі положення максимумів визначається так

,

(1)

адля мінімумів

. (2)

Для світла, що проходить через пластинку умови положення максимумів та мінімумів міняються місцями по відношенню до відбитого світла. Положення максимумів буде визначатися так

, (3)

а для максимумів

. (4)