
умк_Дегтярев_Геодезия_ч.1_2010г
.pdf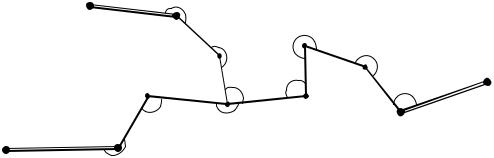
I |
|
II |
|
|
|
III |
А |
Б |
|
Рис. 3.32. Линейно-угловая сеть с одной узловой точкой
Линейно-угловая сеть с одной узловой точкой. Суть обработки за-
ключается в сведении системы ходов с узловой точкой А к трем (по количеству ветвей) отдельным разомкнутым ходам, которые обрабатываются автономно по изложенному выше алгоритму.
При последовательной обработке в первую очередь обрабатываются углы. Для нашего примера каждый ход опирается на исходный пункт с известными координатами и на каждом исходном пункте имеется направление с известным дирекционным углом.
Теперь одну сторону какого-либо хода, проходящую через узловую точку, принимают за узловое направление. Для нашего примера из ветви II сторону А-Б. Вычислим дирекционный угол этой стороны по каждой ветви в отдельности, начиная от начального дирекционного угла: для ветви I – получим αI, для II – αII, для ветви III – дирекционный угол αIII. Если расхождение между максимальным значением и минимальным не более 2′, вычисляют среднее весовое значение из трех. Обусловлено это тем, что длины веток до узлового направления могут быть очень разными, что приводит к разной степени влияния на среднее угла полученного из разных веток. Наиболее просто учесть эту разность условий, это ввести корректирующий множитель за условия (вес), например, в виде:
(3.68)
где ki – количество углов в ходе от исходного направления до узлового направления по соответствующей ветке.
Например, по рис. 3.31, для ветки I – kI = 3, ветки II – kII = 4, ветки III – kIII = 3. Используя (3.68), значение среднего весового для дирекционного угла узлового направления получим как:
αузл. = |
WI αI +WII αII +WIII αIII |
= |
[W α]. |
(3.69) |
|
||||
|
WI +WII +WIII |
[W ] |
|
|
181
Теперь сеть с одной узловой точкой можно разделить на три независимых разомкнутых хода, которые начинаются с исходных пунктов, а заканчиваются узловым направлением с дирекционным углом αузл.. Углы в трех образовавшихся ходах обрабатываются по общей последовательности: невязка, невязка допустимая, поправки, исправленные углы, исправленные дирекционные углы, контроли.
При обработке линейной составляющей сети, по исправленным дирекционным углам каждого из получившихся ходов, вычисляют приращения координат по осям х и у по всем сторонам. По полученным приращениям координат, вычисляют координаты хузл. и уузл. узловой точки А, по ходам I, II и III. По аналогии, среднее весовое из трех значений координат xi и трех значений координаты уi для узловой точки с весами, обратно пропорциональными сумме сторон в соответствующем i-том ходе, вычислим по формулам:
xузл. |
= |
хI WI + хII WII + хIII WIII |
= |
[х W ] |
, |
|
|
||||
|
|
[W ] |
|
|
|||||||
|
|
|
WI +WII +WII |
|
. |
(3.70) |
|||||
|
|
= yI WI + yII WII + yIII WIII = [y W ] |
|||||||||
y |
|
|
|
||||||||
|
узл. |
|
WI +WII +WII |
|
[W ] |
|
|
|
|||
|
|
|
|
|
|
||||||
Здесь веса (коэффициенты влияния) вычисляют как: |
|
|
|
||||||||
|
|
|
W = |
1 |
, |
|
|
|
|
|
(3.71) |
|
|
|
|
|
|
|
|
|
|||
|
|
|
i |
[S ]i |
|
|
|
|
|||
то есть, чем больше длина соответствующего i-того хода [S]i до узловой точки А, тем веса меньше.
Теперь узловую точку А можно считать исходным пунктом с известными координатами и вычислить координатные невязки для хода I, II и III в отдельности. При допустимости невязок вычисляют и вводят поправки в приращения координат по сторонам ходов. По исправленным приращениям координат вычисляют координаты пунктов всех ходов – обычная схема последовательной обработки разомкнутого линейно-углового хода.
Таким образом, основная мысль приближенной обработки линейноугловой сети с одной узловой точкой сводится к разделению системы ходов на отдельные хода, получая в качестве нужных исходных данных значения в виде среднего взвешенного на узле. Такая процедура производится для дирекционных углов и координат. Обработка образовавшихся разомкнутых линейно-угловых ходов проводится по обычной схеме последовательного распределения невязок.
182
Вопросы для контрольной точки по теоретическому материалу модуля 3
1.Основы позиционирования. Определение систем позиционирования.
2.Позиционирование со степенями свободы.
3.Определение положения точек засечками.
4.Определение положения точек ходами. Общие положения.
5.Обработка и оценка точности ориентирного условия при определении положения точек линейно-угловыми ходами.
6.Обработка и оценка точности координатных условий при определении положения точек линейно-угловыми ходами.
ЛАБОРАТОРНАЯ РАБОТА № 4 Методы определения положения точек на плоскости
Цель: изучить способы определения положения точек на плоскости засечками и ходами с оценкой точности результатов.
Время выполнения: 10 часов (5 пар)
Последовательность выполнения
1-1. По данным, выданным преподавателем, получить координаты в локальных базисах двух точек:
а) угловой засечкой; б) линейной засечкой.
2-1. Выполнить оценку точности определения положения точек угловой и линейной засечками, приняв точность линейных измерений – 1/2000, угловых – 30″.
3-2. Обработать полевой журнал измерений в теодолитном ходе, вычислив горизонтальные углы и линии:
а) вычислить горизонтальные углы из полуприемов и среднее; б) проверить качество линейных измерений и вычислить среднее; в) привести линии к горизонту, где это необходимо.
4-2. Выбрать вид передачи исходных данных и произвести соответствующие расчеты:
а) решить обратную геодезическую задачу; б) рассчитать дирекционные углы 2 раза (от двух исходных базисов).
183
5-3. Обработать ориентирное условие теодолитного хода с вычислением исправленных дирекционных углов, контролем по условию и оценкой точности выполнения условия.
а) вычислить угловую невязку и сравнить с допустимой; б) внести поправки в измеренные углы; в) проверить сумму исправленных углов;
г) вычислить исправленные дирекционные углы с контролем условия. 6-4. Обработать координатные условия с оценкой точности:
а) вычислить приращения x и y;
б) вычислить невязки приращений fx и fy;
в) вычислить абсолютную fS и относительную fS /[S ] погрешности и
сравнить с допустимыми значениями; г) вычислить поправки в приращения;
д) вычислить исправленные приращения с контролем сумм; е) вычислить окончательные координаты с контролем выполнения
условий.
7-4. Оценить точность хода в слабом месте.
8-5. Вычислить координаты двух точек определенных засечками (см. п. 1-1 задания) в глобальной системе координат методом сведения к прямой геодезической задаче.
9-5. Трансформировать точки (определенные в п. 1-1 задания) из локального базиса в глобальную систему координат и сравнить с результатами, полученными в п. 8-5 задания.
Состав отчета
1.Описать суть определения координат точек засечками.
2.Схемы и результаты вычислений координат двух точек линейной
иугловой засечками в локальном базисе с оценкой точности результатов.
3.Описать суть определения координат точек теодолитными ходами.
4.Представить полевой журнал с вычисленными углами и линиями.
5.Представить схему привязки с результатами вычислений.
6.Представить координатную ведомость, где отразить:
–обработку ориентирного условия с оценкой точности;
–обработку координатных условий с окончательным вычислением координат, с оценкой точности хода и точки в слабом месте хода.
7.Описать по одному методу выявления грубых угловых и линейных измерений в теодолитном ходе.
184
8.Выявить возможную линейную грубую погрешность в теодолитном ходе по своим невязкам.
9.Представить схемы и результаты вычисления координат точек в глобальном базисе линейной и угловой засечкой.
10.Представить схему и результаты трансформации точек определенных засечками из локального базиса в глобальный.
После выполнения лабораторной работы студент
– должен знать:
1.Суть и методы определения точек засечками.
2.Суть и последовательность обработки результатов измерений для определения точек линейно-угловыми ходами.
3.Суть и последовательность трансформации точек из локального базиса в глобальный.
4.Суть и допуски на оценку точности определения положения точек линейно-угловыми ходами.
– должен уметь:
1.Определить положение точек основными видами засечек в локальном и глобальном базисе с оценкой точности.
2.Трансформировать точки из локального базиса в глобальный.
3.Определить положение точек линейно-угловыми ходами с оценкой точности.
В конце этого модуля студенту выдается расчетно-графическая работа. Работа выполняется студентом самостоятельно при минимальной консультации преподавателя по выданным материалам (см. Приложение).
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА Обработка линейно-угловой сети с одной узловой точкой
Цель: изучить процесс раздельной обработки сети теодолитных ходов с одной узловой точкой.
Время выполнения: самостоятельно в течении трех недель.
Последовательность выполнения
1.Получить индивидуальный вариант задания.
2.Выбрать одно узловое направление и рассчитать его среднее весовое значение, для чего:
– определить из решения обратной геодезической задачи 3 исходных дирекционных угла;
185

–по трем ветвям и результатам измерений рассчитать 3 значения узлового направления;
–рассчитать веса каждой ветки сети через число углов;
–рассчитать среднее весовое узлового направления, если макси-
мальный разброс дирекционных углов не более 2′.
3.Обработать обычным способом с оценкой точности ориентирные (угловые) условия по трем веткам сети, получая все исправленные дирекционные углы.
4.По исправленным дирекционным углам рассчитать по трем веткам средневзвешенные координаты узловой точки, для чего:
–потремветкамрассчитатьприращенияотисходныхточекдоузловой;
–по трем веткам получить три пары координат узловой точки;
–рассчитать веса веток для определения средневзвешенного значения координат;
–рассчитать среднее взвешенное значение координат узловой точки,
если [maxS ] < 20001 .
5. Обработать с оценкой точности fабс и fотн обычным способом координатных условий по трем веткам сети с получением окончательных координат всех точек.
Состав отчета
1.Описать суть и основную последовательность обработки линейноугловой сети с одной узловой точкой.
2.Представить журнал исходных данных.
3.Представить результаты решения трех обратных геодезических задач для получения исходных дирекционных углов.
4.Представить координатную ведомость с результатами обработки условий по трем веткам с оценкой точности. Вычисление весов лучей в условиях представляются на отдельном листе.
После выполнения лабораторной работы студент
– должен знать:
1.Суть и последовательность обработки линейно-угловой сети с одной узловой точкой.
2.Критерии качества обработки.
186
– должен уметь:
1.Рассчитывать веса и средневзвешенные величины при обработке линейно-угловой сети с одной узловой точкой.
2.Оценивать качество обработки.
После выполнения и сдачи студентом лабораторной работы проводится контрольная точка. Для этого ему предлагается дать ответы на 15 вопросов. Звездочкой отмечены вопросы, оцениваемые в 10 %, а все остальные 5 %. При правильном ответе на 15 вопросов студент получает 100 %. При ответах вопросы не переписывают, обязательно указывается фамилия, группа и вариант. Рисунки выполняют схематично, но аккуратно. Не допустимо в качестве ответа записывать одну цифра без пояснений или формул.
Примерный вариант вопросов может быть следующим:
Вариант 111
1.Сколько параметров нужно для определения точек на плоскости?
2.Нарисовать схему угловой засечки.
3.* Записать формулы определения точки засечками методом сведения к прямой геодезической задачи в локальном базисе.
4.* Рассчитать координаты точки в локальном базисе, определяемой угловой засечкой, если длина базиса b = 112,47 м, а измеренные углы
β1 = 67° 16′, β2 = 74° 29′.
5. В каком случае приводят линии к горизонту?
6.* Оценить точность линейных измерений, если измерены длины SП = 117,87 м, SO = 117,82 м и вычислить окончательное значение длины.
7.Что такое привязка геодезических построений?
8.Формула для угловой невязки замкнутого линейно-уголового хода.
9.* Вычислить последующий дирекционный угол, если предыдущий
126° 19′, а левый измеренный 73° 21′.
10.Формулы поправок в приращения координат.
11.Что такое абсолютная невязка.
12.* Рассчитать поправки в приращения x1-2 если все 10 длин достаточно одинаковы, а невязка fx по оси x равна – 0,4 м.
13.Чему равна сумма уравненных приращений?
14.Что такое контроль по выполнению координатного условия при обработке измерений линейно-угловом ходе?
15.Чему равна погрешность определения координат линейно-угло- вого хода в слабом месте?
187
МОДУЛЬ 4
Введение
Четвертый модуль учебно-методического комплекса содержит 3 теоретические темы, 2 лабораторные работы и 2 контрольные точки для проверки теоретических и практических знаний. Из теоретических тем рассмотрены следующие темы:
1.Простейшая трансформация систем координат.
2.Определение высот точек ходами и сетями.
3.Системы координирования в трехмерном пространстве. Лабораторные работы носят названия «Трансформация локальных
координат в глобальные» и «Определение высот точек посредством хода технического нивелирования».
Цель модуля – дать теоретические и практические представления о простейших способах трансформации одной системы координат в другую, получении высот точек через проложение и обработку нивелирных ходов и простейших сетей, системах трехмерного координирования для решения основной цели геодезии.
После изучения модуля студент должен знать:
–общие положения о простейшей трансформации систем координат;
–основные положения, принципы и методы определения высот точек нивелирными ходами и простейшими сетями;
–основные положения о построении и использовании трехмерных систем координирования;
После изучения модуля студент должен уметь:
–выполнять простейшие трансформации систем координат;
–решать прямую и обратную задачу трансформации;
–выполнять определение высот точек по результатам нивелирования
входе;
–выполнять определение высот точек по результатам нивелирования
всети с одной узловой точкой;
–определять и использовать для решения своих задач трехмерные системы координирования;
Контроль усвоения материала производится на основе двух контрольных точек: по теоретическому материалу и по лабораторной работе. По теории предварительно выдается шесть вопросов, на два из которых по вариантам студент должен дать исчерпывающие ответы. По практической части, после того, как лабораторная работа сдана и принята преподавате-
188
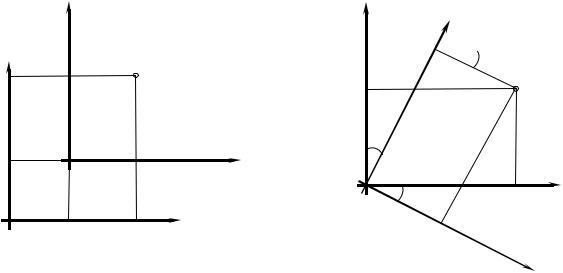
лем, студент письменно отвечает на 15 вопросов, получая оценку в процентах по выполненной правильно части.
На модуль отводится 4 недели – 4 лекции и 4 пары лабораторных занятий (см. календарный план дисциплины).
4.1. Простейшая трансформация систем координат
Основные вопросы: основные элементы трансформации; прямая и обратная задача трансформации; последовательность простейшей трансформации.
Основные элементы трансформации. Достаточно часто координа-
тоопределение производится в разных системах координирования, что обычно вызвано производственной необходимостью. Например, некоторые точки определены в локальном базисе (локальной системе, определенной базисной стороной), а есть необходимость пересчитать их координаты в глобальной системе. В этом случае используется процедура, называемая трансформацией систем координат.
Процедура трансформации для нашего случая может состоять из сдвига локальной системы координат (X′, Y′) относительно глобальной системы (X, Y) (рис. 4.1, а) и вращения одной относительно другой на некоторый угол ϕ (рис. 4.1, б).
|
X′ |
|
|
|
X |
|
C |
|
X′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
X |
|
P |
|
|
|
|
d |
|
x′ |
ϕ |
P |
||
x |
|
x′ |
|
|
c |
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y′ |
Y′ |
|
|
ϕ |
|
|
|
|
|
|
|
|
О′ |
|
|
|
|
|
y |
|
|
|
|||
x |
|
|
|
O |
|
|
ϕ |
|
|
Y |
|||
y |
y Y |
|
|
|
|
y′ |
|
|
|
|
|||
O |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
A |
|
|
a B |
b |
Y′ |
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 4.1. Основные виды трансформации систем координат:
а – трансформация сдвига (трансляция); б – трансформация вращения (ротация)
189
Очевидно, что трансформация сдвига (трансляция) локальной системы координат (X′, Y′) относительно глобальной системы (X, Y) приводит к тому, что локальные координаты точки Р(x′, y′) переходят в глобальные координаты Р(x, y) простым измерением координат на величины x и y
(см. рис. 4.1, а)
′ |
+ |
x; |
|
|
x = x |
(4.1) |
|||
y = y′+ |
y. |
|||
|
||||
Из (4.1) очевидно, что при таком направлении преобразования, величины сдвигов получают как разность глобальных и локальных координат.
Более сложно обстоит дело с трансформацией вращения (ротацией). Обычно вращение производят относительно центра системы координат, для чего сдвигом совмещают центрами обе системы. Такой подход более удобен и нагляден, но не единственный. Таким образом, если есть локальные координаты точки Р(x′, y′) в локальной системе координат (X′, Y′), которая развернута относительно глобальной системы (X, Y) на угол ϕ, а требуется получить глобальные координаты этой точки Р(x, y) в глобальной системе координат (X, Y), поступают следующим образом. Из рис. 4.1, б
можно записать, что глобальные координаты ест: |
|
|
x = c − d; |
(4.2) |
|
y =b + a. |
||
|
Сами же величины отрезков получим из соответствующих прямоугольных треугольников и на основе их подобия.
Из треугольника OCD:
c = x′ cos(ϕ);
(4.3)
b = x′ sin(ϕ).
Из треугольника OAB:
d = y′ sin(ϕ);
(4.4)
a = y′ cos(ϕ).
Тогда, на основе (4.2) и с использованием (4.3), глобальные координаты точки Р(x, y) через локальные Р(x′, y′) можно представить так:
x = c − d = x′ cos(ϕ) − y′ sin(ϕ);
(4.5)
y =b + a = x′ sin(ϕ) + y′ cos(ϕ).
при развороте локальной системы координат (X′, Y′) относительно глобальной системы (X, Y) Очевидно, что формулы (4.5) воспроизводят пово-
190
