умк_Дегтярев_Геодезия_ч.1_2010г

Если невязка не допустима, то проверяют вычисления. Если вычисления верны, то необходимо перемерить углы.

При допустимом значении невязки ее следует распределить путем введения поправок vβi в измеренные углы с целью приведения суммы практической к сумме теоретической и таким образом привести в соответствие геометрическое условие дирекционных углов (3.31). Углы с введенными поправками называют исправленными углами. Исходя из сказанного, можно записать:

откуда следует, что сумма поправок в измеренные углы должна равняться невязке с противоположным знаком:

В выражении (3.37) n неизвестных поправок, и для его решения необходимо наложить на них (n – 1) дополнительных условий. Очевидно, что наиболее простым вариантом таких условий будет равенство всех поправок:

Таким образом, при принятом условии (одним из возможных) угловая невязка fβ распределяется с обратным знаком поровну во все измеренные углы. Исправленные значения углов, исходя из (3.36), вычисляются как:

Проверяем, чтобы сумма исправленных углов равнялась точно сумме углов теоретической по (3.36). Теперь, по исправленным углам поворота вычисляют дирекционные углы всех сторон хода. Выполнение условия (3.36) приводит к совпадению вычисленного и заданного значений конечного исходного дирекционного угла, что является контролем правильности обработки угловых измерений.

Обработка координатных условий. Для получения координатных условий, решим последовательно прямую геодезическую задачу, вычисляя приращения координат xi и yi по каждой стороне хода. Координаты пунктов хода получим по формулам:

171

Сложив левые и правые части, как и для углов, для приращений xi получим:

n

(x1 + x2 +... + xn−1 )+ xкон. = xнач. +(x1 + x2 +... + xn−1 )+ ∑ xi . (3.42)

i=1

После преобразования, имеем формулу математического условия по координате х для разомкнутого линейно-углового хода:

Аналогично рассуждая, получим формулы для координатного условия по координате y:

Очевидно, что из-за погрешностей измерения сторон, суммы вычисленных приращений координат (практические суммы, то, что есть) не будут равны теоретическим суммам (тому, что должно быть). Разность между суммами практическими и суммами теоретическими дают координатные невязки хода:

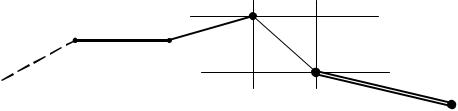
На величины координатных невязок, как и на угловые должны быть наложены допуски, по которым судят о качестве линейных измерений. Но по отдельности для выражений (3.47) сделать это затруднительно, да и не имеет смысла. Для получения величины допуска воспользуемся рис. 3.26.

X nП

Y

fy nТ

Рис. 3.26. Схема определения допуска на координатные условия

172

Здесь, определяя положение 1, 2, …, n – 1, n точки посредством прямой геодезической задачи, мы должны придти в определенную исходную точку nТ, а из-за погрешностей измерений пришли в точку nП. Расхождение в положении точек по координатам x и y дают нам величины невязок fx и fy (см. рис. 3.26). Очевидно, что для общей характеристики погрешности хода целесообразно вычислить длину вектора невязок fS по теореме Пифагора, которая получила название абсолютной погрешности (невязки) хода:

На эту величину, в какой-то мере уже можно наложить допуск, но несложно заметить, что она сильно зависит от длины хода. Абсолютная невязка в 10 см на 1 км хода и на 2 км хода говорит о том, что измерения во втором ходе были выполнены более качественно. Поэтому, в качестве окончательного допуска была принята относительная погрешность (невязка) хода в виде:

Здесь [S] – длина хода;

Мдоп. – знаменатель допустимой относительной погрешности хода. Для теодолитных ходов эта величина в пределах от 1000 до 3000.

Если относительная невязка не в допуске, то проверяют вычисления, а при их верности перемеряют длины линий, при условии что угловая невязка была в пределах допуска.

Допустимые невязки, должны быть уничтожены введением поправок в вычисленные приращения, то есть приведением суммы практической к сумме теоретической. Для этого запишем:

Учитывая, что невязки есть разность между суммой практической и суммой теоретической, из (3.50) имеем:

В этих уравнениях по (n – 1) неизвестных и для их решения необходимо наложить дополнительные условия на поправки vx и vy. Условий на невязки может быть множество. Самые распространенные из них следующие:

– все поправки по координатам для х и у примерно равны. Тогда имеем:

– при измерении длин в ходе лентой, когда погрешность измерения прямо пропорциональна длине, целесообразно невязки распределять пропорционально длине линии

Не сложно заметить, что при длинах примерно равных, (3.53) переходит в (3.52), так как [S] = n S.

Исправленные значения приращений из (3.50) будут:

и сумма исправленных приращений точно равна сумме теоретической, что является контролем вычислений. Другой, окончательный контроль заключается в использовании геометрического условия координат: координаты конечной точки хода (исходного пункта конечного базиса), вычисленные по исправленным приращениям, точно равны значениям этих заданных исходных координат.

По исправленным приращениям, последовательно вычисляют координаты промежуточных точек хода, начиная с первой исходной координаты как:

Общая последовательность обработки. Рассмотренный способ об-

работки измерений в линейно-угловом ходе называют способом последовательного распределения невязок, раздельным способом, нестрогим способом. Строгая обработка линейно-угловых ходов выполняется по методу наименьших квадратов.

Таким образом, обработку результатов измерений для определения положения точек на основе разомкнутого линейно-углового хода можно свести к следующим шагам:

1.Вычисление угловой невязки для оценки по формуле (3.34) и сравнение ее с допуском (3.35) для оценки качества угловых измерений.

2.При допустимом значении невязки вычисляют исправленные углы поворота по (3.40) на основе поправки (3.39). Контроль вычислений (3.36) – сумма исправленных углов точно равна сумме углов теоретиче-

ской (3.32) или (3.33).

174

3.По исправленным углам вычисляют значения дирекционных углов, используя формулы в зависимости от того, какой по ходу угол поворота измерен. Контроль вычислений – конечный дирекционный угол, вычисленный по исправленным углам, должен точно равняться заданному конечному исходному дирекционному углу.

4.На основе формул прямой геодезической задачи, вычисляют приращения по координатам, а по ним невязки (3.47).

5.Качество линейных измерений проверяют на основе допуска (3.49).

6.При выполнении допуска, практические приращения исправляют поправками из формул (3.52) или (3.53) по (3.54). Контроль вычислений (3.50) – сумма исправленных приращений точно равна сумме приращений теоретических (3.45) и (3.46).

7.По исправленным приращениям вычисляют, последовательно используя прямую геодезическую задачу, координаты всех точек хода (3.55). Контроль вычислений – координаты конечной точки хода (она же исходная точка), вычисленные по исправленным приращениям, должны точно равняться заданным координатам конечной исходной точки.

Обработка результатов в замкнутом ходе. Обработка результатов измерений для определения положения точек, выполненного по схеме замкнутого (сомкнутого) хода выполняется по шагам, определенным выше, но с некоторыми различиями. Отличие состоит в вычислении теоретических сумм углов и приращений координат. В замкнутом ходе для вычисления суммы углов теоретической (см. рис. 3.24, б, формулы (3.32) или (3.33)) начальный и конечный исходные дирекционные углы совпадают, что приводит к уменьшению числа используемых углов поворота на 2. Окончательно для суммы имеем:

[β]Т = 180° (n – 2). (3.56)

Очевидно, формула работает с внутренними углами и известна из геометрии. Если измерялись внешние углы, то для суммы теоретической получим:

Все последующие вычисления совершенно аналогичны шагам для обработки в разомкнутом ходе.

Несложно заметить, что вся обработка сводится к уничтожению возникших из-за наличия избыточных измерений и погрешностей измерений несоответствий в геометрических условиях, если результаты измерений качественны (невязки в допуске).

Некоторые способы выявления грубых погрешностей в измере-

ниях. После уравнивания одиночного линейно-углового хода ошибки положения его пунктов неодинаковы. Они возрастают от начала и конца хода к его середине, и наибольшую ошибку положения имеет пункт в середине хода. В случае приближенного уравнивания эта ошибка оценивается половиной абсолютной невязки хода fs.

Если относительная невязка (3.49) намного больше допуска, то предполагается, что в одном из линейных измерений допущена грубая погрешность. Один промах в линейных измерениях находится чрезвычайно просто исходя из рис. 3.27. Здесь сторона S имеет грубую погрешность , которая в полной мере входит в значение абсолютной невязки fS. Из формулы

Рис. 3.27. Схема выявления грубой линейной погрешности

Таким образом, из формулы для абсолютной невязки (3.48) и рис. 3.27, имеем ее длину и направление:

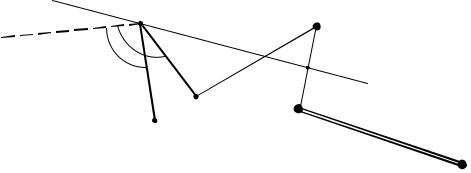
Знак «приближенно» стоит здесь потому, что другие погрешности тоже вносят вклад в формирование абсолютной невязки, но величина намного значительнее. Найдя в ведомости сторону, дирекционный угол которой ближе всего к значению угла, полученного по (3.60) можно сказать, что погрешность в длине именно в этой стороне, только если она одна.

Есть некоторые возможности также определить одну грубую погрешность в угле, но для этого необходимо иметь графическое представление абсолютной невязки и все точки хода, нанесенные на план по координатам. Если (рис. 3.28) вместо угла β измерен угол β′ = β + , вместо нужной точки k приходим в точку k′ с искажением всех последующих точек. Это искажение носит поперечный характер (в отличие от грубых погрешностей в линейных измерениях, которые носят продольный характер), что приводит к возникновению большой величины абсолютной невязки fS. Имея графическое представление как на рис. 3.28, для нахождения грубого углового измерения, поступают следующим образом:

–графически находят середину вектора абсолютной невязки fS (рис. 3.28) как точку t;

–проводят через найденную середину перпендикуляр l, направление которого и укажет на плохо измеренную вершину угла.

Рис. 3.28. Схема выявления грубого углового измерения

Аналитический способ поиска одного грубо измеренного угла заключается в том, чтобы просчитать координаты точек 1, 2, 3 в ходе по часовой стрелке (рис. 3.29) и против часовой стрелки 3, 2, 1. В вершине, где будет грубое угловое измерение, например, точке 2, вместо угла 1-2-3 прямо будет использован угол 1-2-3′, а обратно 3-2-1′. Очевидно, что координаты прямо и обратно максимально совпадут именно в этой точке, так как только после ее происходит разворот хода на величину грубой погрешности .

177

2

1

3

1′

3′

Рис. 3.29. Схема выявления грубой угловой погрешности аналитически

Другие способы обработки.

Процесс обработки может быть сведен и к другой схеме:

– вычисляют угловую невязку, просчитывая все промежуточные дирекционные углы как:

– при выполнении допуска, вычисленные дирекционные углы исправляются поправками, пропорциональными номеру стороны i хода в n точек:

Понятно, что в последний дирекционный угол войдет вся невязка с противоположным знаком;

– по исправленным дирекционным углам считают приращения (как промежуточные величины, а не основные) и координаты всех точек хода, по которым получают координатные невязки

– если невязки в допуске исправляют координаты, вводя в них последовательно поправки, пропорционально распределяя невязки по соответствующим координатам. Пропорциональность возможна или относительно номера точки, или длины стороны с накоплением. В последнюю координату вводится вся невязка с противоположным знаком. Например, в первую вычисленную координату х вводится поправка:

и так далее.

178

Возможен также графический (графоаналитический) способ обработки, суть которого в следующем (рис. 3.30):

–получают координаты всех точек хода на основе прямой геодезической задачи без исправления углов. Имея вычисленные координаты исходной точки в конце хода, вычисляют невязки и сравнивают их с допустимыми значениями;

–по значениям невязок по координатам fx и fу вычисляют величину абсолютной невязки fS и ее направление;

–теперь необходимо все текущие точки хода 1, 2 и т.д. сдвинуть в направлении невязки на величины, пропорциональные по какому либо правилу величине абсолютной невязки fS. Обычно распределяют пропорционально накопленной сумме сторон, или длинам замыкающих. Проще всего это сделать графически. При аналитическом способе, единственная возможность – разложить вектор сдвига на составляющие по координатам х и у и таким образом, исправить текущие координаты, как в предыдущем способе.

Рис. 3.30. Схема графоаналитического способа обработки измерений в ходе

179

3.6. Определение положения точек сетями

Основные вопросы: общие положения; линейно-угловая сеть с одной узловой точкой.

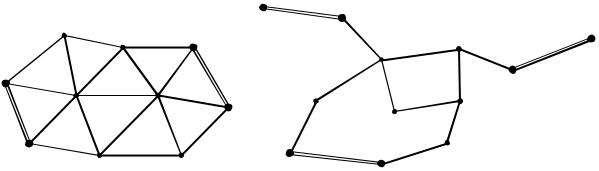
Общие положения. При определении положения точек, образующих поле, проложение через них хода весьма затруднительно. В этом случае засечки используют не последовательно, а последовательно-параллельно. Это приводит к тому, что из одной точки может быть произведено не одно измерение, а несколько, на другие соседние точки. Такого рода точки называют узловыми, а подобные построения получили название геодезические сети, или система геодезических ходов. Системы из звеньев триангуляции и трилатерации (рис. 3.31, а) в последнее время потеряли свою значимость. Поэтому мы будем рассматривать системы из линейно-угловых ходов, или линейно-угловые сети (рис. 3.31, б).

Рис. 3.31. Схемы систем ходов:

а – сеть триангуляции (трилатерации), б – линейно-угловая сеть

Несложно понять, что произвольные линейно-угловые сети (например, вида представленного на рис. 3.31, б) обработать по приведенному ранее алгоритму (последовательное распределение невязок) достаточно трудоемко. Такие построения обрабатывают на основе строгих методов по методу наименьших квадратов (МНК), который изучается в теории математической обработки геодезических измерений. Но есть несложные ли- нейно-угловые сети, которые можно обработать и по приближенным алгоритмам без существенной потери точности. К таким построениям относят линейно-угловую сеть с одной узловой точкой (рис. 3.32).

180