М.А. Можейко

СЕЧЕНОВ Иван Михайлович (1829--1905) -- русский физиолог и психолог. Почетный член Петербургской Академии наук (1904). Основные сочинения: “Кому и как разрабатывать психологию” (1873), “Элементы мысли” (1878), “Предметная мысль и действительность” (1892), “Впечатления и действительность” (1890), “Очерк рабочих движений человека” (1901) и др. С. выдвинул программу построения новой психологии, опирающейся на объективный метод и принцип изучения развития психики в реальных жизненных встречах организма со средой, разработал систему взглядов на организм и его психические функции. С. предвосхитил понятие об обратной связи как непременном регуляторе поведения, утвердил новое понимание саморегуляции и системы организации нервно-психической деятельности, обосновал новый подход к функциям органов чувств. В работе “Рефлексы головного мозга” (1863) С. дает естественно-научный анализ деятельности мозга. С. раскрыл причинную обусловленность психических явлений внешними воздействиями, показал, что психика есть результат протекания физиологических процессов возбуждения и торможения в коре мозга, регулятор внешних воздействий и поведения в целом. Переориентация исследовательской мысли с внутреннего “пространства” сознания, открытого для наблюдающего за ним субъекта, на психически регулируемое поведение, открытое для опытной объективной науки, -- величайшая заслуга С. Основой такой переориентации стал рефлекс, трактуемый С. как согласование движения с выполняющим сигнальную роль чувствованием. Учение о рефлексе и физиология органов чувств явились основой объективной психологии. Все сеченовские открытия проецировались на определенную систему философских идей. Открытие центрального торможения исходило, и в свою очередь, обосновывало позиции детерминизма, давало конкретно-научный материал для обоснования проблемы свободы воли. Открытие сенсорных “снарядов” и механизмов построения чувственного образа стало естественно-научной демонстрацией идеи о соответствии познавательного процесса свойствам объектов, формирующих его “ткань”. Внутренняя связь философских и естественно-научных идей, отличающая работы С., определила глубину его учения, которое было воспринято Павловым, Выготским, Бехтеревым и др.

Т.В. Самущик

СИЛЛОГИЗМ (греч. syllogismos -- сосчитывание) -- дедуктивное умозаключение, в котором из двух посылок, связанных одним общим термином, делается заключение. В качестве посылок и вывода С. выступают высказывания: общеутвердительные („Все S есть P“), общеотрицательные („Ни одно S не есть P“), частноутвердительные („Некоторые S есть P“), частноотрицательные („Некоторые S не есть P“), где S (субъект) -- предмет мысли, P (предикат) -- признак, приписываемый предмету мысли. По традиции, идущей от Аристотеля -- создателя теории С., вывод, основанный на логической связи между данными высказываниями, обозначаемыми соответственно A, E, I, O (гласные буквы из латинских слов „affirmo“ -- утверждаю, „nego“ -- отрицаю), называется простым категорическим С. (ПКС). Понятия, которые составляют посылки или заключение С., называются терминами С. Правильно построенный С. состоит из трех терминов: 1) меньшего термина (S) -- субъекта заключения; 2) большего термина (Р) -- предиката заключения; 3) среднего термина (М), присутствующего в обеих посылках, но отсутствующего в заключении.

Все планеты (М) светят отраженным светом (Р).

Венера (S) -- планета (М).

Венера (S) светит отраженным светом (Р).

Высказывание, в котором находится меньший термин, называется меньшей посылкой. Высказывание, в котором находится больший термин, называется большей посылкой. Два главных типа отношений между терминами С., на которых основана логическая необходимость вывода, раскрываются в аксиоме С.: все, что утверждается (отрицается) относительно всего множества, утверждается (отрицается) относительно каждого его элемента. Данный аксиоматический принцип тесно связан с другим принципом, имеющим латинское название nota notae -- „признак признака“: признак признака предмета есть признак самого предмета. То, что отрицается относительно признака предмета, отрицается и относительно самого предмета. Данные аксиомы формируются соответственно для объема и содержания терминов. Из истинных посылок нельзя сделать истинное заключение, если не выполняются общие правила категорического С. Общие правила С. делятся на правила терминов и правила посылок. Правила терминов: 1) в каждом ПКС должно быть только три термина. При нарушении данного правила возникает ошибка „учетверения термина“; 2) средний термин должен быть распределен, т.е. взят во всем объеме, по крайней мере, в одной из посылок; 3) термин, не распределенный ни в одной из посылок, не может быть распределен в заключении. Правила посылок: 4) одна из посылок должна быть общим высказыванием, т.к. из двух частных посылок ничего не следует; 5) одна из посылок должна быть утвердительным высказыванием, т.к. из двух отрицательных посылок ничего не следует; 6) если одна из посылок -- частное высказывание, то и заключение должно быть частным; 7) если одна из посылок -- отрицательное высказывание, то и заключение должно быть отрицательным; 8) из двух утвердительных посылок нельзя сделать отрицательное заключение. По расположению среднего термина различают четыре фигуры ПКС. В первой фигуре ПКС средний термин расположен на месте субъекта в большой посылке и на месте предиката в меньшей посылке:

Все исчезающие виды животных (М) заносятся в красную книгу (Р)

Зубр (S) -- исчезающий вид (М).

Зубр (S) занесен в Красную книгу (P)

Логическая схема первой фигуры ПКС: . Правила первой фигуры ПКС: 1) большая посылка должна быть общим высказыванием; 2) меньшая посылка должна быть утвердительным высказыванием. Во второй фигуре ПКС средний термин расположен на месте предиката в обеих посылках:

Все растения, произрастающие в данной местности (Р), цветут (М).

Папоротник (S) не цветет (М).

Папоротник (S) не растет в данной местности (P).

Логическая схема второй фигуры ПКС: . Правила второй фигуры ПКС: 1) большая посылка должна быть общим высказыванием; 2) одна из посылок должна быть отрицательным высказыванием. В третьей фигуре ПКС средний термин расположен на месте субъекта в обеих посылках:

Курение (М) опасно для здоровья (Р).

Курение (М) -- порок (S).

Некоторые пороки (S) -- опасны для здоровья (P).

Логическая схема третьей фигуры ПКС: . Правила третьей фигуры ПКС: 1) меньшая посылка должна быть утвердительным высказыванием; 2) заключение должно быть частным высказыванием. В четвертой фигуре ПКС средний термин расположен на месте предиката в большей посылке и на месте субъекта в меньшей посылке:

Квадрат (Р) -- ромб (М).

Все ромбы (М) -- параллелограммы (S).

Некоторые параллелограммы (S) -- квадраты (Р).

Логическая схема четвертой фигуры ПКС: . Правила четвертой фигуры ПКС: 1) если одна из посылок -- отрицательное высказывание, то большая посылка должна быть общим высказыванием; 2) если большая посылка -- утвердительное высказывание, то меньшая должна быть общим высказыванием; 3) если меньшая посылка -- утвердительное высказывание, то заключение должно быть частным высказыванием. Четвертая фигура ПКС используется в практике вывода редко. Ее сводят обычно к первой фигуре ПКС. Разновидности фигур ПКС, отличающиеся друг от друга качественной и количественными характеристиками высказываний, являющихся посылками и заключением, называются модусами фигур ПКС. Для каждой фигуры ПКС можно построить 64 (4 в третьей степени) модуса (ибо 4 -- количество всех простых высказываний (A, E, I, O), 3 -- количество высказываний, допускаемых в ПКС (две посылки и заключение)). Для четырёх модусов ПКС можно построить 256 модусов (64х4=256). Модусы фигур ПКС делятся на правильные, построенные в соответствии с общими правилами С. и специальными правилами фигур, и неправильные. Из 256 логически правильными являются 24 модуса, среди которых 19 сильных и 5 слабых модусов. Слабый модус С. отличается от соответствующего сильного модуса наличием частного заключения (с квантором „некоторый“) вместо общего (с квантором „все“). Правильные сильные модусы первой фигуры: AAA, EAE, AII, EIO; второй фигуры: EAE, AEE, EIO, AOO; третьей фигуры: AAI, IAI, AII, EAO, OAO, EIO; четвертой фигуры: AAI, AEE, IAI, EAO, EIO. Правильные слабые модусы первой фигуры: AAI, EAO; второй фигуры: EAO, AEO; четв¸ртой фигуры: AEO. Современная теория C. включает другие виды дедуктивных выводов, логический анализ которых не проводился в аристотелевской логике. Речь идет о силлогистических выводах из посылок, одна из которых, по крайней мере, является сложным высказыванием. Различают: 1) разделительно-категорические С. (РКС); 2) условно-категорические С. (УКС); 3) чисто условные С. (ЧУС); 4) эквивалентно-категорические С. (ЭКС). Разделительно-категорическим называется С., одна из посылок которого разделительное (дизъюнктивное) высказывание, другая — категорическое высказывание. Различают два правильных модуса РКС: 1) утверждающе-отрицающий, в котором ход рассуждения направлен от утверждения одних аргументов исключающей дизъюнкции к отрицанию остальных:

Углы могут быть острыми, тупыми или прямыми.

Данный угол острый.

Данный угол не является ни тупым, ни прямым.

Логические схемы утверждающе-отрицающего модуса РКС: ;.; 2) отрицающе-утверждающий, в котором ход рассуждения направлен от отрицания одних аргументов дизъюнкции к утверждению остальных. Характер дизъюнкции -- исключающий или неисключающий, значения не имеет:

Иванов сдал экзамены по философии или логике.

Иванов еще не сдал экзамен по философии.

Иванов сдал экзамен по логике.

Логические схемы отрицающе-утверждающего модуса РКС: ; . Условно-категорическим называется С., одна из посылок которого условное (импликативное) высказывание, другая -- категорическое высказывание. Различают два правильных модуса УКС: 1) утверждающий, в котором из истинности основания импликации делается вывод об истинности ее следствия, но не наоборот:

Если углы вертикальны, то они равны.

Данные углы вертикальны.

Данные углы равны.

Логическая схема утверждающего модуса УКС: . 2) отрицающий, в котором из ложности следствия импликации делается вывод о ложности ее основания, но не наоборот:

Если число делится на 4, то оно делится на 2.

Данное число не делится на 2.

Данное число не делится на 4.

Логическая схема отрицающего модуса УКС: . Чисто условным называется С., в котором обе посылки условные (импликативные) высказывания. Заключение первой посылки является основанием второй посылки:

Если число целое, то оно рациональное.

Если число рациональное, то оно действительное.

Если число целое, то оно действительное.

Логическая схема ЧУС:. Эквивалентно-категорическим называется С., одна из посылок которого -- эквивалентное высказывание, другая -- категорическое. Различают два модуса ЭКС: 1) утверждающий, в котором из истинности одного высказывания делается вывод об истинности другого высказывания:

Число делится на 3, если и только если сумма цифр,

составляющих данное число, делится на 3.

Сумма цифр, составляющих данное число, делится на 3.

Данное число делится на 3

Логические схемы утверждающего модуса ЭКС: ; ; 2) отрицающий, в котором из ложности одного высказывания делается вывод о ложности другого:

Магнитное поле вокруг проводника возникает, если и только если по нему течет ток.

Магнитное поле вокруг проводника не возникло.

По проводнику ток не течёт.

Логические схемы отрицающего модуса ЭК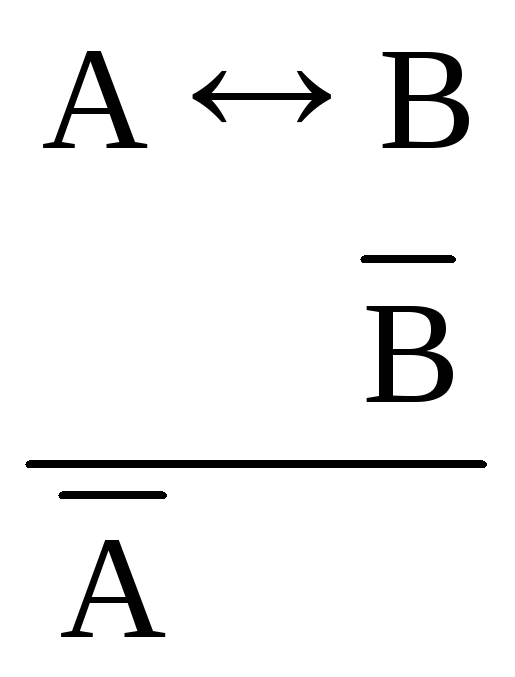С: ; . Из простых (с двумя посылками) С. образуются сложные С. В основе их логического анализа лежит анализ простых С.