
- •Математическое моделирование Учебное пособие
- •Донецк 2006
- •Содержание
- •Введение
- •1. Построение экспериментальных законов распределения
- •1.1. Общие положения
- •1.2. Статистические критерии согласия
- •Г) Критерий согласия Романовского
- •1.3. Построение закона Пуассона
- •1.4. Построение показательного закона
- •1.5. Построение нормального закона
- •2. Модели оптимизации
- •2.1. Принципы формирования моделей оптимизации
- •Задача производственного планирования
- •Задача оптимальной загрузки оборудования
- •Задача о смесях
- •Транспортная задача
- •2.2. Графический метод решения задачи линейного программирования
- •Алгоритм графического метода решения злп
- •2.3. Универсальный метод решения линейных задач оптимизации
- •Алгоритм симплекс-метода решения злп
- •Пример 2.3.1. Решить злп (2.2.1), (2.2.5) симплекс-методом.
- •Критерий оптимальности опорного плана
- •Переход к следующей симплекс-таблице осуществляют по правилам:
- •2.4. Двойственная задача линейного программирования
- •Свойства двойственных задач
- •2.5. Методы анализа конфликтных ситуаций с помощью матричных игр
- •Алгоритм принципа максимина (минимакса)
- •Решение. Этаматричная игра имеет размерность (3х4), т.Е. Игрок а имеет три стратегии, а игрок в – четыре. Запишем ее в нормальной форме.
- •Последовательность действий при решении игры
- •3. Регрессионный анализ
- •3.1. Однофакторные модели
- •3.1.1. Построение однофакторных моделей
- •3.1.2. Оценка качества моделей
- •Свойства коэффициента корреляции
- •Построение доверительного интервала для прогнозного значения
- •Пример 3.1.Исследовать зависимость объема прибыли от количества торговых точек. Сделать прогноз в предположении, что количество торговых точек будет увеличено до 25.
- •Вспомогательная расчетная таблица
- •Пример 3.2.Исследовать зависимость показателяуи факторахс помощью логарифмической, степенной и полиномиальной регрессий.
- •3.1.3. Модели рядов динамики
- •3.2. Автокорреляция данных и остатков
- •3.2.1. Автокорреляция данных
- •Пример 3.4. Исследовать на автокорреляцию динамический ряд:
- •Вспомогательная таблица для расчета коэффициента автокорреляции
- •3.2.2. Автокорреляция остатков
- •Причины возникновения автокорреляции
- •Вспомогательная таблица для расчета d-статистики
- •С помощью формулы (3.2.2) найдем d -статистику:
- •3.3. Мультиколлинеарность
- •Причины возникновения мультиколлинеарности:
- •Методы исследования мультиколлинеарности
- •Меры по устранению мультиколлинеарности:
- •3.4. Множественная линейная регрессия
- •3.4.1. Построение множественной линейной регрессии
- •Расчет элементов коэффициента
- •3.4.2. Матричный подход
- •Построение корреляционной матрицы
- •Построение модели множественной линейной регрессии и ее анализ
- •3.4.4. Нелинейные модели
- •3.4.5. Эластичность
- •4.Экспертные оценки и элементы теории графов
- •4.1. Ранговая корреляция
- •4.1.1. Экспертное оценивание
- •4.1.2. Этапы работ в системе экспертных оценок
- •4.1.3. Метод ранговой корреляции
- •Вспомогательные расчеты
- •Б) Случай многих экспертов
- •4.2. Элементы сетевого планирования
- •Основные элементы сетевого графика
- •Основные требования к сетевой модели
- •5. Индивидуальные задания для самостоятельной работы студентов по курсу “математическое моделирование”
- •5.1. Задания к разделу “Построение законов распределения”
- •5.2. Задания к разделу “Математическое программирование”
- •5.3. Задания к разделу “Регрессионный анализ”
- •Задание 2.
- •Задание 3.
- •5.4. Задания к разделу “Экспертные оценки и элементы теории графов” Задание 1.
- •Значение критерия Пирсона
- •Критерий Колмогорова
- •Критерий Колмогорова
- •Квантили распределения Стьюдента
- •Коефициентов автокорреляции
- •Литература
- •Пеніна Галина Геннадіївна, канд. Екон. Наук, доцент
Причины возникновения мультиколлинеарности:
в модель включены факторные признаки, характеризующие одну и ту же сторону явления;
уравнение регрессии содержит в качестве факторных признаков такие показатели, суммарное значение которые представляет собой постоянную величину;
в модели использованы факторные признаки, являющиеся составными элементами друг друга;
в моделирующую функцию включены факторные признаки, по смыслу дублирующие друг друга.
Проблема мультиколлинеарности является обычной для регрессии временных рядов, т.е. когда данные состоят из ряда наблюдений в течение некоторого периода времени. Если две или более объясняющие переменные имеют ярко выраженной временной тренд, то они будут тесно коррелированы, и это может привести к мультиколлинеарности.
Если среди парных коэффициентов корреляции независимых переменных существуют такие, значение которых приближается или равно множественному коэффициенту корреляции, то это говорит о возможности существования мультиколлинеарности.
Если
в эконометрической модели получено
малое значение параметра
![]() при большом коэффициенте детерминации
при большом коэффициенте детерминации![]() и при этом
и при этом![]() -критерий
существенно отличается от нуля, то это
говорит о наличии мультиколлинеарности.
-критерий
существенно отличается от нуля, то это
говорит о наличии мультиколлинеарности.
Методы исследования мультиколлинеарности
нахождение и анализ корреляционной матрицы
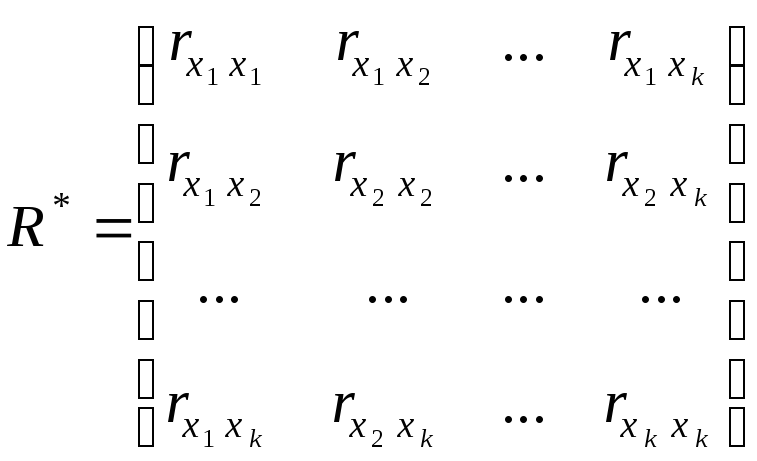
Стохастическая связь между переменными характеризуется величиной коэффициента корреляции между ними. Чем ближе по абсолютной величине значение коэффициента корреляции к единице, тем сильнее мультиколлинеарность. В общем случае, если при оценке уравнения регрессии несколько факторов оказались незначимыми, то нужно выяснить нет ли среди них коррелированных между собой. Для этого формируется матрица коэффициентов парной корреляции, которая является симметричной и называется корреляционной матрицей. Она имеет вид:
 ,
(3.3.1)
,
(3.3.1)
 ,
(3.3.2)
,
(3.3.2)
где
![]() - коэффициенты парной корреляции между
переменнойуи одним из факторов,
- коэффициенты парной корреляции между
переменнойуи одним из факторов,![]() - коэффициенты парной корреляции между
факторами, которые вычисляются по
формуле
- коэффициенты парной корреляции между
факторами, которые вычисляются по
формуле
![]() , (3.3.3)
, (3.3.3)
где
![]() ,
,![]() ,
,![]() .
.
Анализ корреляционной матрицы позволяет оценить, во-первых, степень влияния отдельных факторов на результативный показатель, во-вторых, взаимосвязь факторов между собой.
Если коэффициенты парной корреляции между некоторыми факторами близки к единице, это указывает на тесную взаимосвязь между ними, т.е. на наличие мультиколлинеарности. В этом случае один из факторов необходимо исключить из дальнейшего рассмотрения. Встает вопрос, какой именно. Это зависит от конкретной ситуации. Чаще всего для моделирования оставляют тот фактор, который с экономической точки зрения более весом для изучаемого процесса. Можно также оставить фактор, который имеет большее влияние на результативный показатель (т.е. коэффициент корреляции которого с результативным показателем больше). Такого рода анализ проводится для каждой пары факторов. Результатом анализа корреляционной матрицы является установление группы факторов, мало зависимых между собой – они и должны входить в модель.
вычисление определителя корреляционной матрицы
Если в модели больше двух факторов,
вопрос о мультиколлинеарности не может
ограничиваться информацией, которую
дает корреляционная матрица. Более
широкая проверка предусматривает
вычисление определителя матрицы
![]() ,
,![]() .
Если
.
Если![]() ,
то существует полная мультиколлинеарность.
Если
,
то существует полная мультиколлинеарность.
Если![]() ,
то мультиколлинеарности нет. Чем ближе
,
то мультиколлинеарности нет. Чем ближе![]() к нулю, тем увереннее можно утверждать
о существовании между переменными
мультиколлинеарности.
к нулю, тем увереннее можно утверждать
о существовании между переменными
мультиколлинеарности.
метод Феррара-Глаубера
Для исследования общей мультиколлинеарности
и мультиколлинеар-ности между отдельными
факторами используется корреляционная
матрица
![]() ,
вычисляемая по формуле (3.3.2).
,
вычисляемая по формуле (3.3.2).
Для исследования общей мультиколлинеарности
используется критерий
![]() .
Рассчитывается величина
.
Рассчитывается величина
![]() ,
(3.3.4)
,
(3.3.4)
имеющая
![]() - распределение с
- распределение с![]() степенями свободы.
степенями свободы.
По данной надёжности
![]() и числу степеней свободы
и числу степеней свободы![]() находят табличное значение
находят табличное значение![]() (приложение А). Если
(приложение А). Если![]() ,
то можно считать, что мультиколлинеарность
между объясняющими переменными
отсутствует.
,
то можно считать, что мультиколлинеарность
между объясняющими переменными
отсутствует.
Если
![]() ,
то с заданной надёжностью
,
то с заданной надёжностью![]() можно считать, что между факторами
существует общая мультиколлинеарность.
можно считать, что между факторами
существует общая мультиколлинеарность.
Далее исследуется, какая объясняющая переменная порождает мультиколлинеарность, и решается вопрос об ее исключении из дальнейшего анализа.
Для выяснения вопроса,
между какими факторами существует
мультиколлинеарность, используется
![]() -статистика
или
-статистика
или![]() -статистика.
Для этой цели используют частные
коэффициенты парной корреляции
-статистика.
Для этой цели используют частные
коэффициенты парной корреляции![]()
![]() между объясняющими переменными, которые
вычисляют по формуле
между объясняющими переменными, которые
вычисляют по формуле
![]() ,
(3.3.5)
,
(3.3.5)
где
![]() – элементы обратной матрицы
– элементы обратной матрицы![]() .
.
В качестве критерия используется величина
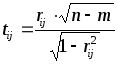 ,
(3.3.6)
,
(3.3.6)
имеющая
распределение Стьюдента с
![]() степенями свободы.
степенями свободы.
По таблицам Стьюдента (приложение Д)
находят критическое значение
![]() .
Сравнивают критическое значение
.
Сравнивают критическое значение![]() с расчетным
с расчетным![]() :
:
если
 ,
то между объясняющими переменными
,
то между объясняющими переменными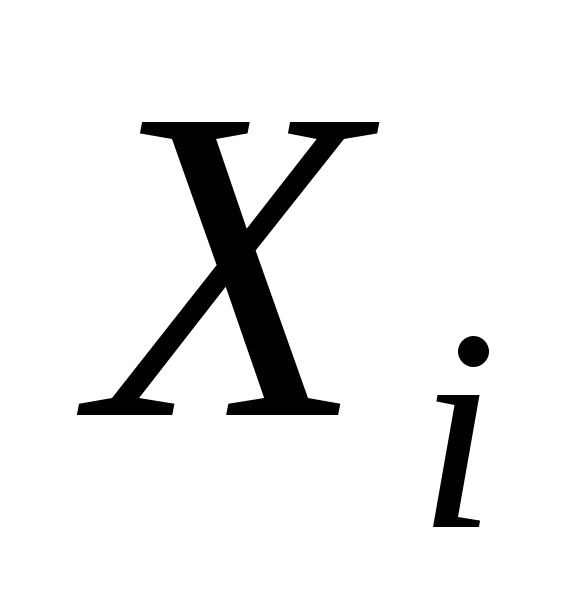 и
и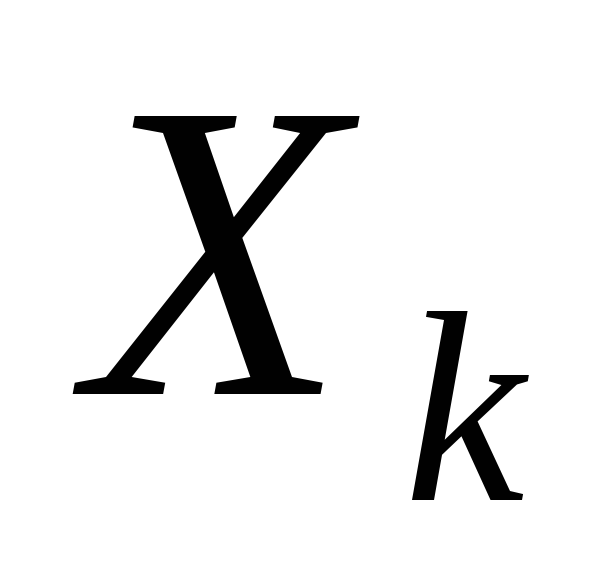 коллинеарности нет.
коллинеарности нет.если
 ,
то между объясняющими переменными
,
то между объясняющими переменными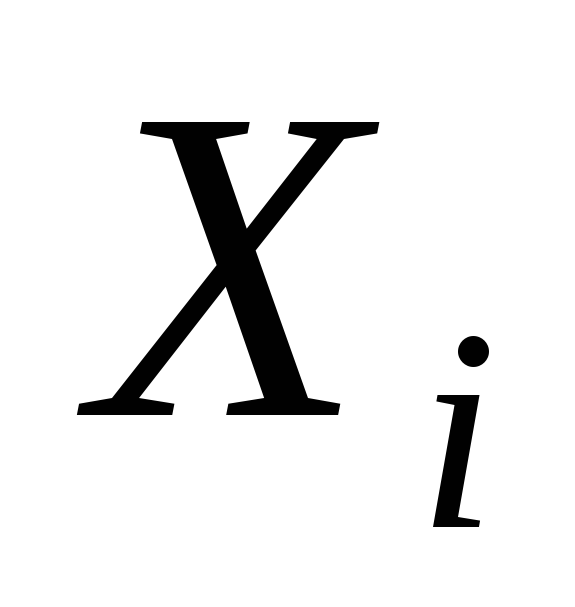 и
и существует значительная коллинеарность..
существует значительная коллинеарность..
|
Замечание. |
В случае выявления коллинеарности
между парой объясняющих переменных
|
Методы устранения мультиколлинеарности
Если мультиколлинеарность выявлена, необходимо предпринять ряд мер по ее уменьшению и возможному устранению. Необходимо знать, что безошибочных и абсолютно правильных рекомендаций нет, это процесс творческого поиска. Все зависит от степени мультиколлинеарности, от набора факторов, от характера данных.
Различные методы, которые могут быть использованы для смягчения мультиколлинеарности, связаны с информационной базой и делятся на две категории. К первой относятся попытки повысить степень надежности оценок регрессии – увеличить число наблюдений в выборке, за счет сокращения временного периода увеличить дисперсию объясняющих переменных и снизить вариацию случайного числа, уточнить набор объясняющих переменных, включаемых в модель. Ко второй категории относится использование внешней информации, т.е. сбор дополнительных данных и оценок.
метод исключения переменных
Этот метод заключается в том, что высоко
коррелированные объясняющие переменные
устраняются из регрессии, и она заново
оценивается. Отбор переменных, подлежащих
исключению, производится с помощью
коэффициентов корреляции. Для этого
производится оценка значимости
коэффициентов парной корреляции
![]() между объясняющими переменными
между объясняющими переменными![]() и
и![]()
![]() .
Если
.
Если![]() ,
то одну из переменных можно исключить.
Но какую переменную удалить из анализа,
решают исходя из экономических
соображений.
,
то одну из переменных можно исключить.
Но какую переменную удалить из анализа,
решают исходя из экономических
соображений.
метод линейного преобразования переменных
Этот метод устранения мультиколлинеарности
заключается в переходе к регрессии
приведенной формы путем замены переменных,
которым присуща коллинеарность, их
линейной комбинацией. Если между двумя
факторами
![]() и
и![]() существует мультиколлинеарность, то
заменяют фактор
существует мультиколлинеарность, то
заменяют фактор![]() после чего проверяют наличие
мультиколлинеарности между факторами
после чего проверяют наличие
мультиколлинеарности между факторами![]() и
и![]() .
При отсутствии мультиколлинеарности
вместо фактора
.
При отсутствии мультиколлинеарности
вместо фактора![]() рассматривается фактор
рассматривается фактор![]() .
.
метод пошаговой регрессии
Процедура применения пошаговой регрессии начинается с построения простой регрессии. В анализ последовательно включают по одной объясняющей переменной. На каждом шаге проверяется значимость коэффициентов регрессии и оценивается мультиколлинеарность переменных. Если оценка коэффициента получается незначимой, то переменная исключается и рассматривают другую объясняющую переменную. Если оценка коэффициента регрессии значима, а мультиколлинеарность отсутствует, то в анализ включают следующую переменную. Таким образом, постепенно определяются все составляющие регрессии без нарушения положения об отсутствии мультиколлинеарности.
